Примеры решения задач типового расчёта 2 страница

-1/2

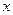
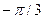0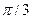

Задача 5

Задача 5

Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0,8 мм. Считая, что случайная величина Х распределена нормально со средним квадратическим отклонением 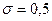мм, составить формулу дифференциальной функции (плотности вероятностей) 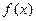и найти, сколько в среднем будет годных шариков среди ста изготовленных.

Решение

1. Дифференциальная функция нормального распределения определяется формулой

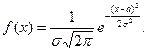
Так как Х – отклонение (диаметра шарика от проектного размера), то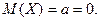

Подставляя параметры 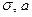в формулу плотности вероятности, получим

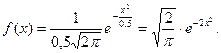
2. Воспользуемся формулой

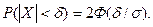
Подставив сюда 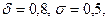получим

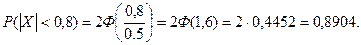
Таким образом, вероятность отклонения, меньшего 0,8 мм, равна 0,8904. Оотсюда следует, что примерно 89 шариков из ста окажутся годными.

Задача 6

Построить гистограмму относительных частот по данному распределению выборки объёма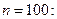

частичный интервал 0-2 2-4 4-6

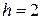
сумма частот вариант 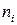20 30 50

частичного интервала

Решение

Найдём относительные частоты:

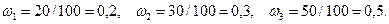
Найдём плотности относительных частот, учитывая, что длина интервала :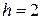

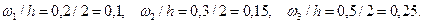
Построим на оси абсцисс данные частичные интервалы.

Проведём над этими интервалами отрезки на расстояниях, равных соответствующим плотностям относительной частоты:

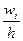
0,25

0,15

0,1

0 2 4 6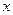

Так выглядит искомая гистограмма относительных частот.

Задача 7

Найти доверительный интервал для оценки с надёжностью 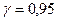неизвестного математического ожидания 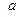нормально распределённого признака Х генеральной совокупности, если генеральное среднее квадратическое отклонение 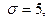выборочная средняя 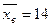и объём выборки 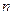=25.

Решение

Искомый доверительный интервал найдём по формуле

.

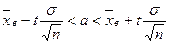Все величины, кроме 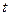, известны. Найдём 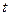из соотношения 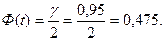По таблице приложения (см. часть 1) 2 находим 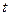=1,96. Подставив значения 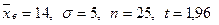в указанную формулу, получим

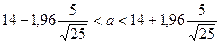или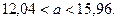

Интервал (12,04;15,96) покрывает исследуемый параметр 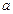с надёжностью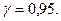
Условия задач типового расчёта

Вариант 1

1. Вероятность выигрыша в лотерее 0,05. Некто покупает 5 билетов. Составить закон распределения дискретной случайной величины Х- – числа выигрышных билетов среди купленных. Построить полигон распределения, график интегральной функции. Найти числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.

2. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Составить закон распределения Ддискретнойая случайнойая величинаы Х – числоа вызовов за две минуты. Вычислить вероятности возможных значений Х=0,1,2,3,4. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение. Поток вызовов предполагается простейшим (применить формулу Пуассона) . Возможные значения Х принять в интервале 0…4.

3. Вероятность появления события в каждом испытании равна 0,25. Используя неравенство Чебышева, оценить вероятность того, что число Х появлений события заключено в пределах от 150 до 250, если было произведено 800 испытаний.

4. Дана дифференциальная функция непрерывной случайной величины Х:

.

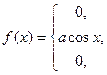
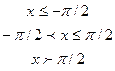Найти параметр 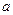, вероятность попадания случайной величины Х в интервал

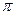(- /4, 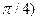, математическое ожидание, дисперсию и среднее квадратическое

отклоненение. Построить графики дифференциальной и интегральной функций.

5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра

шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением 0,4 мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.

6. Построить гистограмму относительных частот по данному распределению выборки

объёма :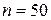

частичный интервал 0-2 2-4 4-6 6-8 8-10

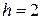
сумма частот вариант 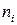5 10 18 12 5

частичного интервала

5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра

шарика от проектного размера по абсолютной величине меньше 0,7мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением 0,4мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.

7. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением 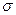=3. Найти доверительный интервал для оценки неизвестного математического ожидания 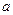, если выборочная средняя 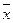=4,2, объём выборки 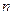=36, а надёжность оценки 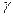=0,95.

Вариант 2

1.1. Вероятность выигрыша в лотерее 0,04. Некто покупает 3 билета. Составить закон рас - пределения дискретной случайной величины Х – числа выигрышных билетов среди купленных. Построить полигон распределения, график интегральной функции. Найти числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.

2. Среднее число вызовов, поступающих на АТС в одну минуту, равно трём. Дискретная случайная величина Х – число вызовов за полторы минуты. Вычислить вероятности возможных значений Х=0,1,2,3,4. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.

Среднее число вызовов, поступающих на АТС в одну минуту, равно трём. Составить закон распределения дискретной случайной величины Х – числа вызовов за полторы минуты. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение. Поток вызовов предполагается простейшим (применить формулу Пуассона) . Возможные значения Х принять в интервале 0…5.

3. Вероятность появления события в каждом испытании равна 0,5. Используя неравенство неравенство Чебышева, оценить вероятность того, что число Х появлений события заключено в пределах от 40 до 60, если было произведено 100 испытаний.

4. Дана дифференциальная функция непрерывной случайной величины Х:

.

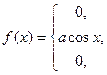
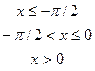Найти параметр 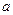, вероятность попадания случайной величины Х в интервал (-- 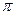/4,;0), , математическое ожидание, дисперсию и среднее квадратическое отклонение. Построить графики дифференциальной и интегральной функций.

5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра

шарика от проектного размера по абсолютной величине меньше 0,3 2мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением 0,32 мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.

6. Построить гистограмму относительных частот по данному распределению выборки

объёма :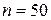

частичный интервал 0-3 3-6 6-9 9-12 12-15

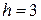
сумма частот вариант 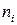4 11 18 13 4

частичного интервала

7. Случайная величина Х имеет нормальное распределение с известным средним квадрати-ческим отклонением 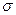=2. Найти доверительный интервал для оценки неизвестного математического ожидания 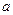, если выборочная средняя 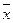=5,3, объём выборки 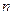=64, а надёжность оценки 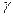=0,99.

Вариант 3

1. Вероятность выигрыша в лотерее 0,03. Некто покупает 3 билета. Составить закон распределения дискретной случайной величины Х – числа выигрышных билетов среди купленнных. Построить полигон распределения, график интегральной функции. Найти числовые характеристики – математическое ожидание, дисперсию, среднее квадратичес- кое квадратическое отклонение.

1.

2. Среднее число вызовов, поступающих на АТС в одну минуту, равно одному. Дискретная случайная величина Х – число вызовов за две минуты. Вычислить вероятности возможных значений Х=0,1,2,3,4. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.

2.1.Среднее число вызовов, поступающих на АТС в одну минуту, равно трём. Составить закон распределения дискретной случайной величины Х – числа вызовов за полторы минуты. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение. Поток вызовов предполагается простейшим (применить формулу Пуассона) . Возможные значения Х принять в интервале 0…5.

3. Вероятность появления события в каждом испытании равна 0,3. Используя неравенство Чебышева, оценить вероятность того, что число Х появлений события заключено в пределах от 50 до 70, если было произведено 200 испытаний.

4. Дана дифференциальная функция непрерывной случайной величины Х:

.

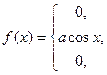
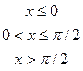Найти параметр 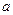, вероятность попадания случайной величины Х в интервал

(0, 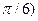, математическое ожидание, дисперсию и среднее квадратическое отклонение. Построить графики дифференциальной и интегральной функций.

6. Построить гистограмму относительных частот по данному распределению выборки

объёма :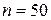

частичный интервал 0-5 5-10 10-15 15-20 20-25

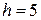
сумма частот вариант 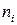6 9 18 11 6

частичного интервала

5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра

шарика от проектного размера по абсолютной величине меньше 0,4 мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением 0,25 мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.

5, Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра

шарика от проектного размера по абсолютной величине меньше 0,3мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением 0,4мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.

7. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением 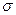=3. Найти доверительный интервал для оценки неизвестного математического ожидания 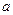, если выборочная средняя 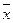=6,4, объём выборки 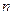=81, а надёжность оценки 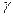=0,95.

Вариант 4

1. Вероятность выигрыша в лотерее 0,06. Некто покупает 5 билетов. Составить закон распределения дискретной случайной величины Х – числа выигрышных билетов среди купленных. Построить полигон распределения, график интегральной функции. Найти числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.

2. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Дискретная случайная величина Х – число вызовов за полторы минуты. Вычислить вероятности возможных значений Х=0,1,2,3,4. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.

Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Составить закон распределения дискретной случайной величины Х – числа вызовов за полторы минуты. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение. Поток вызовов предполагается простейшим (применить формулу Пуассона) . Возможные значения Х принять в интервале 0…3.

3. Вероятность появления события в каждом испытании равна 0,25. Используя неравенство Чебышева, оценить вероятность того, что число Х появлений события заключено в пределах от 65 до 85, если было произведено 300 испытаний.

4. Дана дифференциальная функция непрерывной случайной величины Х:

.

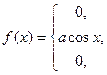
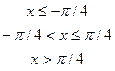Найти параметр 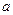, вероятность попадания случайной величины Х в интервал

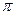(- /6, 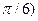, математическое ожидание, дисперсию и среднее квадратическое отклонение. Построить графики дифференциальной и интегральной функций.

6. Построить гистограмму относительных частот по данному распределению выборки

объёма :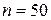

частичный интервал 3-5 5-7 7-9 9-11 11-13

сумма частот вариант 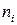4 8 20 10 8

частичного интервала

5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра

шарика от проектного размера по абсолютной величине меньше 0,4мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением 0,5 мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных. 5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра

шарика от проектного размера по абсолютной величине меньше 0,5 мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением 0,4 мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.

7. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением 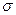=4. Найти доверительный интервал для оценки неизвестного математического ожидания 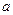, если выборочная средняя 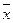=7,5, объём выборки 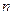=100, а надёжность оценки 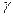=0,999.

Вариант 5

1. Вероятность выигрыша в лотерее 0,07. Некто покупает 3 билета. Составить закон распределения дискретной случайной величины Х – числа выигрышных билетов среди купленных. Построить полигон распределения, график интегральной функции. Найти ччисисловые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.

2. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум с половиной. Дискретная случайная величина Х – число вызовов за две минуты. Вычислить вероятности возможных значений Х=0,1,2,3,4. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.

Среднее число вызовов, поступающих на АТС в одну минуту, равно четырём. Составить закон распределения дискретной случайной величины Х – числа вызовов за одну минуту. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение. Поток вызовов предполагается простейшим (применить формулу Пуассона) . Возможные значения Х принять в интервале 0…4.

3. Вероятность появления события в каждом испытании равна 0,2. Используя неравенство Чебышева, оценить вероятность того, что число Х появлений события заключено в пределах от 60 до 90, если было произведено 400 испытаний.

4. Дана дифференциальная функция непрерывной случайной величины Х:

.

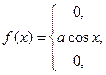
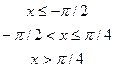Найти параметр 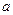, вероятность попадания случайной величины Х в интервал

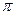(- /3, 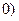, математическое ожидание, дисперсию и среднее квадратическое отклонение. Построить графики дифференциальной и интегральной функций.

5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра

шарика от проектного размера по абсолютной величине меньше 0,5мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением 0,7мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра

шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением 0,5 мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.

6. Построить гистограмму относительных частот по данному распределению выборки