Границы применимости закона Дарси

Закон Дарси справедлив при соблюдении следующих условий:

a) пористая среда мелкозерниста и поровые каналы достаточно узки;

b) скорость фильтрации и градиент давления малы;

с) изменение скорости фильтрации и градиента давления малы.

При повышении скорости движения жидкости закон Дарси нарушается из-за увеличения потерь давления на эффекты, связанные с инерционными силами: образование вихрей, зон срыва потока с поверхности частиц, гидравлический удар о частицы и т.д. Это так называемая верхняя граница. Закон Дарси может нарушаться и при очень малых скоростях фильтрации в процессе начала движения жидкости из-за проявления неньютоновских реологических свойств жидкости и её взаимодействия с твёрдым скелетом пористой среды. Это нижняя граница.

Верхняя граница. Критерием верхней границы справедливости закона Дарси обычно служит сопоставление числа РейнольдсаRe=war/h с его критическим значением Re_кр, после которого линейная связь между потерей напора и расходом нарушается. В выражении для числа Re:

w-характерная скорость течения:

а - характерный геометрический размер пористой среды;

r - плотность жидкости.

Имеется ряд представлений чисел Рейнольдса, полученных различными авторами при том или ином обосновании характерных параметров. Приведём некоторые из данных зависимостей наиболее употребляемые в подземной гидромеханике:

а) Павловского

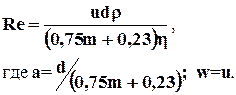(1.30)

Критическое число РейнольдсаRe_кр=7,5-9.

б) Щелкачёва

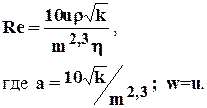(1.31)

Критическое число Рейнольдса Re_кр=1-12.

в) Миллионщикова

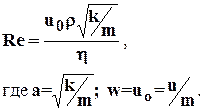(1.32)

Критическое число Рейнольдса Re_кр=0,022-0,29.

Скорость фильтрации u_кр, при которой нарушается закон Дарси, называется критической скоростью фильтрации. Нарушение скорости фильтрации не означает перехода от ламинарного движения к турбулентному, а вызвано тем, что силы инерции, возникающие в жидкости за счёт извилистости каналов и изменения площади сечения, становятся при u>u_кр соизмеримы с силами трения.

При обработке экспериментальных данных для определения критической скорости пользуются безразмерным параметром Дарси:

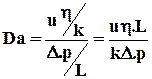, (1.33)

представляющим отношение сил вязкого трения к силе давления. В области действия закона Дарси данный параметр равен 1 и уменьшается при превышении числа Re критического значения.

Нижняя граница. При очень малых скоростях с ростом градиента давления (изменение давления с глубиной) увеличение скорости фильтрации происходит более быстро, чем по закону Дарси. Данное явление объясняется тем, что при малых скоростях становится существенным силовое взаимодействие между твердым скелетом и жидкостью за счет образования аномальных, неньютоновских систем, н.п. устойчивые коллоидные растворы в виде студнеобразных плёнок, перекрывающих поры и разрушающихся при некотором градиенте давленияt_н , называемого начальным и зависящим от доли глинистого материала и величины остаточной водонасыщенности. Имеется много реологических моделей неньютоновских жидкостей, наиболее простой их них является модель с предельным градиентом

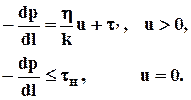(1.34)

1.3.1.4. Законы фильтрации при Re > Re_кр

От точности используемого закона фильтрации зависит достоверность данных исследования скважин и определение параметров пласта. В связи с этим в области нарушения действия закона Дарси необходимо введение более общих, нелинейных законов фильтрации. Данные законы разделяются на одночленные и двухчленные.

Одночленные законы описываются степенной зависимостью вида

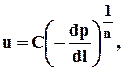(1.35)

где C, n - постоянные, 1£ n £ 2.

Данные зависимости не удобны, т.к. параметр nв общем случае зависит от скорости фильтрации. В связи с этим наибольшее употребление нашли двухчленные зависимости, дающие плавный переход от закона Дарси к квадратичному, называемому формулой Краснопольского:

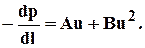(1.36)

КоэффициентыА и Вопределяются либо экспериментально, либо теоретически. В последнем случае

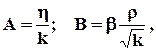(1.37)

где b - структурный коэффициент и по Минскому определяется выражением

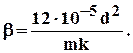
Трещиноватая среда

Линейный закон фильтрации

В трещиноватых пластах скорость фильтрации связана со средней скоростью через трещиноватость

u=m_тw. (1.39)

Средняя скорость выражается через градиент давления по формуле Буссинеска при представлении течения по трещинам, как течения между двумя плоскими параллельными пластинами

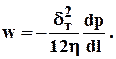(1.40)

Если использовать зависимости (1.39), (1.17), то получим линейный закон фильтрации в трещиноватых средах:

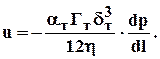(1.41)

По аналогии с законом Дарси проницаемость трещиноватых сред равна

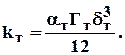(1.42)

Для трещиновато-пористой среды общая проницаемость определяется как сумма межзерновой и трещинной проницаемостей.

В разделе 1.2.3.2. отмечалась необходимость рассмотрения трещинно-пористой среды как деформируемой. При таком подходе проницаемость трещинного пласта будет также изменяться с изменением давления, а именно:

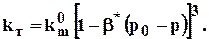(1.43)

Необходимо отметить, что данная зависимость справедлива при небольших изменениях давления. В более общем случае необходимо использовать экспоненциальную связь деформации трещин с давлением.