Занятие 9. Смешанное произведение трех векторов

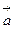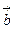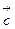Пусть даны три вектора , и . Если вектор 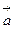векторно умножается на 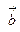, а затем получившийся вектор 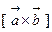скалярно умножается на вектор 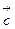, то получается число, называемое смешанным произведением векторов , , .

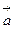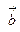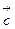Теорема. Смешанное произведение 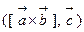равно объему параллелепипеда, построенного на приведенных к общему началу векторах 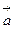, 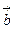и 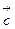, взятому со знаком (+), если тройка 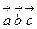правая, и со знаком (-) , если тройка 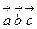левая. Если же векторы 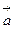, 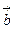и 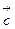компланарны, то .

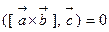Следствие 1. Справедливо равенство

.

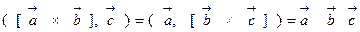Следствие 2. Необходимым и достаточным условиемкомпланарности трех векторов является равенство нулю их смешанного произведения.

Следствие 3. Смешанное произведение трех векторов, два из которых совпадают, равно нулю. (Такие три вектора заведомо компланарны).

Теорема. Если три вектора 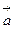, 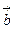и 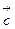определены своими декартовыми прямоугольными координатами 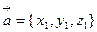, , 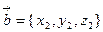, 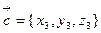то смешанное произведение 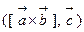равняется определителю, строки которого соответственно равны координатам перемножаемых векторов, то есть

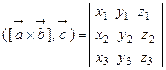(9.1)

Пример 9.1. Доказать, что векторы 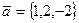, , 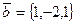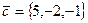компланарны.

Решение. Найдем смешанное произведение этих векторов по формуле:

.

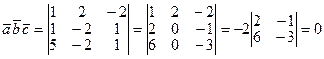. Это и означает, что векторы 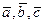компланарны.

Пример 9.2. Даны вершины тетраэдра: 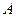(0, -2, 5), 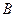(6, 6, 0), 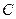(3, -3, 6), 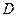(2, -1, 3). Найти длину его высоты, опущенной из вершины .

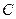Решение. Найдем сначала объем тетраэдра 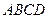. По формуле получаем:

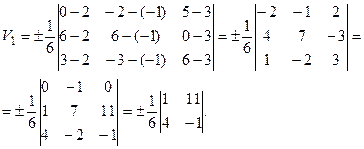
Так как определитель равен отрицательному числу, то в данном случае перед формулой нужно взять знак минус. Следовательно, .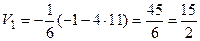

Искомую величину h определим из формулы 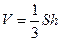, где S – площадь основания. Определим площадь S: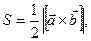

где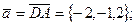

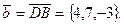
Поскольку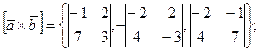

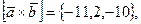
то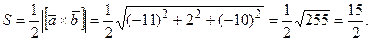

Подставляя в формулу 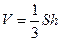значения 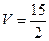и 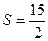, получим h=3.

Пример 9.3.Образуют ли векторы 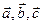базис в пространстве ? Разложить вектор 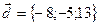по базису векторов .

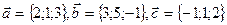Решение. Если векторы образуют базис в пространстве, то они не лежат в одной плоскости, т.е. являются некомпланарными. Найдем смешанное произведение векторов : ,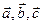

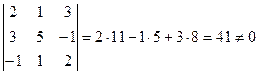следовательно векторы некомпланарны и образуют базис в пространстве. Если векторы образуют базис в пространстве, то любой вектор 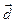можно представить в виде линейной комбинации базисных векторов , а именно ,

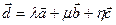где 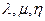координаты вектора 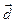в базисе векторов 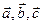. Найдем эти координаты, составив и решив систему уравнений

.

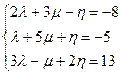Решая ее методом Гаусса, имеем

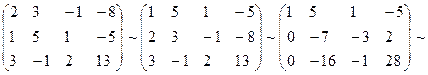
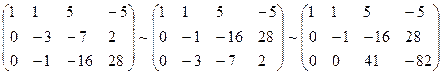
Отсюда 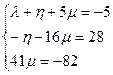. Тогда .

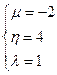Таким образом, .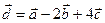

Вопросы для самопроверки

1. Что называется смешанным произведением трех векторов, каковы его свойства?

2. Как смешанное произведение выражается через координаты векторов-сомножителей?

3.Какому условию должны удовлетворять координаты трех векторов, чтобы их можно было принять за базис пространства?