А) Вычисление объема тела по известным площадям параллельных сечений.

ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.

ПЛАН

1. Геометрические и приложения.

2. Физические приложения.

Вычисление площадей плоских фигур

А) Вычисление площадей в прямоугольной системе координат.

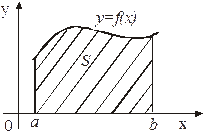1. Если функция неотрицательна на

отрезке , то площадь криволинейной

трапеции, ограниченной кривой ,

прямыми 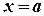, 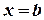и (рис. 1),

вычисляется по формуле:

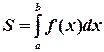. (1) Рис. 1

Формула (1) справедлива на основании геометрического смысла определенного интеграла.

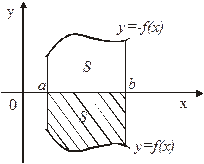
2. Если функция - неположительна

на , то площадь S (рис. 2)

вычисляется по формуле:

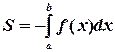. (2)

Действительно, отражая кривую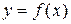

относительно оси абсцисс, получаем

кривую с уравнением 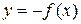, которая Рис. 2

уже неотрицательна на отрезке 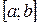, а площадь под нею из соображений симметрии равна площади S (рис. 2). Тогда .

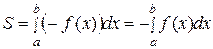3. Если 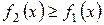и непрерывны на отрезке 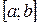, то площадь S фигуры,

заключенной между кривым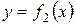и и 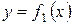на этом отрезке

(рис. 3) определяется формулой:

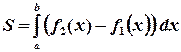. (3)

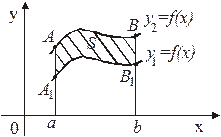
Рис. 3

4. Если плоская фигура имеет «сложную»

форму, то прямыми, параллельными оси

Оу, ее следует разбить на части так, чтобы

можно было бы применить уже известные

формулы.

Так площадь области S, изображенной

на рисунке 4, может быть найдена Рис. 4

следующим образом:

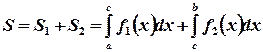. (4)

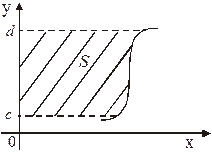
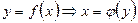5. Если криволинейная трапеция ограничена

прямым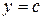и и 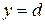, осью Оу и непрерыв-

ной функцией 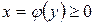(рис. 5), то

ее площадь вычисляется по формуле:

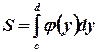. (5) Рис. 5

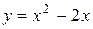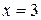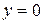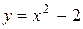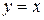Пример 1. Найти площадь фигуры, ограниченной линиями: а) , , ; б) , ; в) , , , .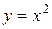

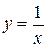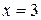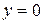Решение.

а) 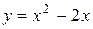, , 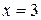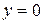. Заданная фигура ограничена параболой с уравнением 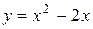, прямой, параллельной оси ординат ( 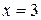) и осью абсцисс ( ) (рис. 6).

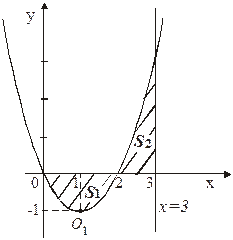
Рис.6

Как видно из рис. 6, площадь фигуры S равна сумме площаде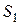й и 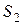, для нахождения которых применяем формулы (2) и (1), соответственно: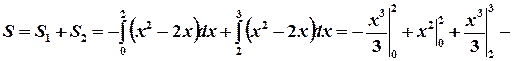

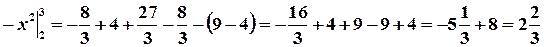(ед²).

б) , .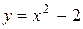

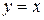Фигура имеет вид, изображенный на рис. 7.

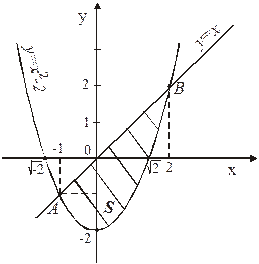
Рис. 7

Найдем координаты точек пересечения параболы 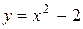и прямой 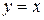, решив систему этих уравнений 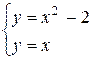, А(-1; -1), В(2; 2). Абсциссы точек А и В пересечения этих линий задают пределы интегрирования.

Так как на отрезке 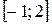график функции 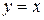расположен «выше», чем график функции 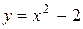, т.е. выполняется неравенство 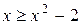, то для нахождения площади фигуры S воспользуемся формулой (3), полагая :

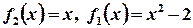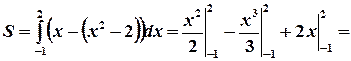
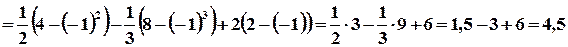(ед²).

в) , , , .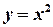

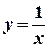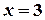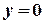Фигура имеет вид изображенный на рис. 8.

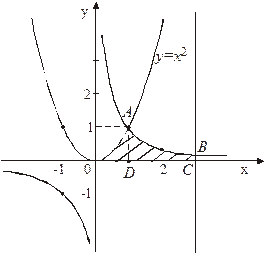
Рис. 8

Линия, ограничивающая фигуру сверху, состоит из части ОА параболы 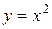и части АВ гиперболы 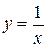. Следовательно, площадь S найдем как сумму двух площадей: 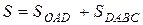, используя формулу (4).

Решая систему 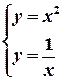найдем координаты точки А(1; 1).

Тогда 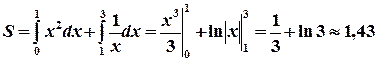(ед²).

Вычисление объемов тел

а) Вычисление объема тела по известным площадям параллельных сечений.

Пусть имеется некоторое тело Т. Предположим, что известна площадь любого сечения этого тела плоскостью, перпендикулярной к оси Ох (рис. 9).

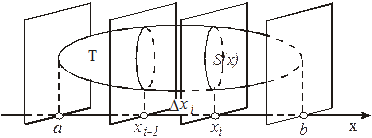
Рис. 9

Эта площадь будет зависеть от положения секущей плоскости, т.е. будет функцией от х: 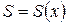, где .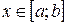

Предположим, что 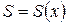- непрерывная функция, тогда объем данного тела можно вычислить по формуле:

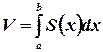. (6)

Формулу (6) называют формулой объема тела по известной площади поперечного сечения.

Б) Объем тела вращения.

Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией 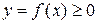, отрезком 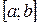оси Ох и прямым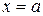и и 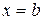(рис. 9).

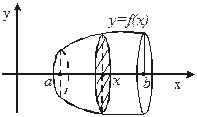
Рис. 9

Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох 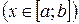, есть круг с радиусом .

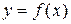Следовательно, 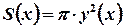. Применяя формулу (6) объема тела по площади параллельных сечений, получаем

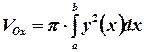. (7)

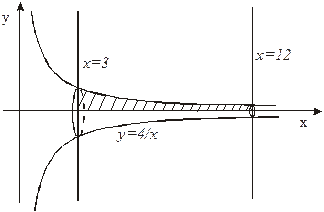Пример 2. Вычислить объем тела,

которое получается при вращении

вокруг оси Охкриволинейной тра-

пеции, ограниченной гиперболой

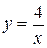, прямыми 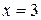, х = 12 и

осью абсцисс.

Решение. Построим фигуру,

ограниченную заданными ли-

ниями, а затем тело вращения

вокруг оси Ох (рис. 10). Рис. 10

По формуле (7) имеем

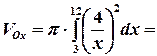
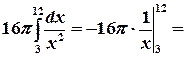
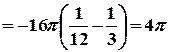(ед³.).