Логарифмическое ( логнормальное ) распределение
Случайная величина  имеет логарифмическое нормальное распределение с параметрами a и
имеет логарифмическое нормальное распределение с параметрами a и 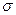 , если случайная величина ln x имеет нормальное распределение с параметрами a >и
, если случайная величина ln x имеет нормальное распределение с параметрами a >и 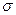 .
.
Функция плотности вероятностей логнормального распределения имеет вид:
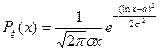
Распределение Парето.
Применяется при анализе дохода и других экономических индексов.
Плотность вероятностей для случайной величины, распределенной по Парето, имеет вид
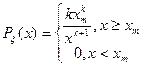
Z-распределение Фишера.
Плотность вероятностей для случайной величины имеет вид:
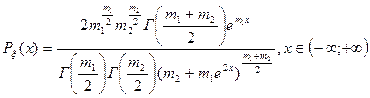
26. Распределение Вейбулла – Гнеденко.
Широко используется при оценках надежности и риска.
Случайная величина  имеет распределение Вейбулла с параметрами
имеет распределение Вейбулла с параметрами 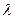 и k , если ее функция распределения:
и k , если ее функция распределения:
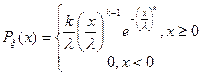
Полиномиальное распределение (мультиномиальное распределение).
Совместное распределение вероятностей случайных величин

принимающих целые неотрицательные значения

удовлетворяющие условиям
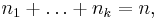
с вероятностями
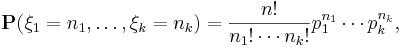
где 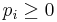 ,
, 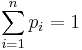 ; является многомерным дискретным распределением случайного вектора
; является многомерным дискретным распределением случайного вектора  такого, что :
такого, что : 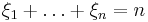 (по существу это распределение является (k − 1)-мерным, так как в пространстве
(по существу это распределение является (k − 1)-мерным, так как в пространстве 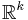 оно вырождено); естественным (с точки зрения современной теории вероятностей)
оно вырождено); естественным (с точки зрения современной теории вероятностей)
1.  Вырожденное распределение.
Вырожденное распределение.
Говорят, что случайная величина 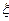 имеет вырожденное распределение в точке a
имеет вырожденное распределение в точке a 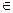 R, если
R, если  принимает единственное значение a с вероятностью 1, т.е. P(
принимает единственное значение a с вероятностью 1, т.е. P(  =a)=1.
=a)=1.
Функция распределения  имеет вид
имеет вид
F  (x) = P (
(x) = P (  <x) =P(a<x) =
<x) =P(a<x) = 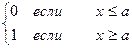
Параметры:
1.Математическое ожидание
M(x) = 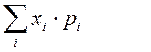
M(x) = a∙1=a
2.Дисперсия
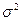 =M(
=M(  -a)
-a) 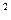 =
= 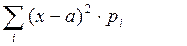
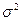 =(a-a)
=(a-a) 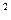 ∙1=0
∙1=0
3.Характеристическая функция
f 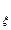 (t)=
(t)= 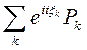
f 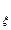 (t)=
(t)= 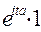 =
= 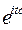
4.Начальный момент r-го порядка
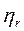 =
= 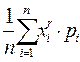 , r=1,2,3,…
, r=1,2,3,…
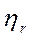 =
= 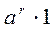 =
= 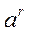
5.Абсолютный момент r-го порядка
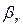 =M(│x│
=M(│x│ 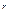 )=
)= 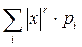
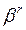 =
= 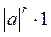 =
= 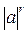
6.Факториальный момент r-го порядка
f  =M(x
=M(x 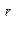 ) =
) = 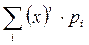
f  =
= 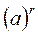
7.Центральный момент r-го порядка
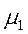 =
= 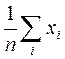
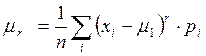
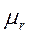 =(a-a)
=(a-a) 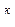 ∙1=0
∙1=0
8.Медиана
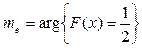
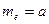
9.Мода
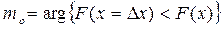
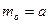
Распределение Бернулли.
Говорят, что случайная величина  имеет распределение Бернулли с параметром p , если
имеет распределение Бернулли с параметром p , если  принимает значения 1 и 0 с вероятностями p и 1-p=q соответственно. Случайная величина
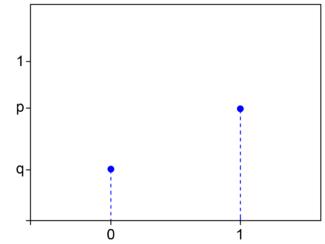
принимает значения 1 и 0 с вероятностями p и 1-p=q соответственно. Случайная величина  с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха p : ни одного успеха или один успех. Таблица распределения
с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха p : ни одного успеха или один успех. Таблица распределения  имеет вид:
имеет вид:
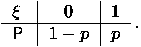
Функция распределения случайной величины  такова:
такова:
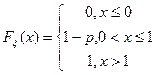
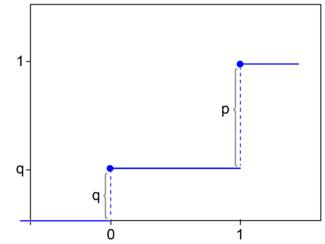
Параметры:
1.Математическое ожидание
M(x) = 0∙(1-p)+1∙p=p
2.Дисперсия
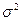 =(0-p)
=(0-p) 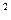 ∙(1-p)+(1-p)
∙(1-p)+(1-p) 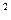 ∙p=(p)
∙p=(p) 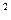 ∙(1-p)+(1-p)
∙(1-p)+(1-p) 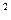 ∙p=(1-p)∙( p
∙p=(1-p)∙( p 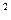 +(1-p) ∙p)=p- p
+(1-p) ∙p)=p- p 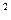 =pq
=pq
3.Характеристическая функция
f 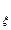 (t)=
(t)= 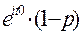 +
+ 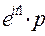 = 1-p+
= 1-p+ 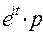 =q+
=q+ 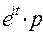
4.Начальный момент r-го порядка
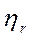 =
= 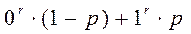 =p
=p
5.Абсолютный момент r-го порядка
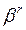 =p
=p
6.Факториальный момент r-го порядка
f  =p
=p
7.Центральный момент r-го порядка
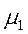 =
= 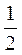
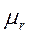 = (0-
= (0- 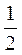 )
) 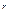 ∙(1-p)+ (1-
∙(1-p)+ (1- 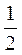 )
) 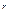 ∙p=(
∙p=( 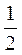 )
) 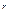 ∙(1-p+p)= (0.5)
∙(1-p+p)= (0.5) 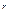
8.Медиана
нет
9.Мода
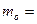 max(p,q)
max(p,q)
