Свойства функций, непрерывных на отрезке. Равномерная непрерывность функции
Функция f(x) называется непрерывной на [a,b], если она непрерывна в каждой точке интервала (a,b), а также является непрерывной справа в точке a и непрерывной слева в точке b.
Теорема 1 (Вейерштрасс: об ограниченности непрерывной на отрезке функции). Если функция f(x) непрерывна на отрезке [a,b], то она ограничена на нем.
gТребуется установить, что ($c>0): ("xÎ[a,b]®½f(x)½£c). (1)
Предположим противное, т.е. ("c>0) ($xcÎ[a,b]) : ½f(xc)½>c. (2)
Полагая в соотношении (2) c=1,2, …, n, … получим, что ("nÎN) ($xnÎ[a,b]) : ½f(xn)½>n. (3)
Из условия ("nÎN)®a£xn£b имеем, что последовательность {xn} ограничена. По теореме Больцано-Вейерштрасса из нее можно выделить сходящуюся подпоследовательность: ${ 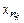 }:
}: 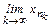 =x. (4)
=x. (4)
В силу условия (3): ("kÎN) ® a£ 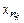 £b. (5)
£b. (5)
Тогда из условий (4) и (5) по теореме о предельном переходе в неравенстве получаем xÎ[a,b]. функция f непрерывна, поэтому из условия (4) имеем: 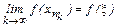 . (6)
. (6)
С другой стороны, утверждение (3) выполняется ("nÎN): в частности, при n=nk (k=1,2,…), т.е. 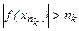 . Последнее означает:
. Последнее означает: 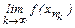 =+¥, так как при k®¥ также n®¥. Это противоречит условию (6), согласно которому последовательность значений функции
=+¥, так как при k®¥ также n®¥. Это противоречит условию (6), согласно которому последовательность значений функции 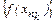 имеет конечный предел. Условие (2) не выполнимо и справедливо утверждение (1).n
имеет конечный предел. Условие (2) не выполнимо и справедливо утверждение (1).n
Теорема 2(Вейерштрасс: о достижении точных граней непрерывной на отрезке функции). Если функция f(x) непрерывна на [a,b], то она достигает на нем своих точных граней, т.е.:
($ x, hÎ[a,b]) : ( f(x)= 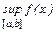 Ù f(h)=
Ù f(h)= 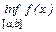 ). (7)
). (7)
gПо теореме 1 функция f(x) ограничена, а у всякого ограниченного множества E(f) существуют точные грани: 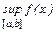 =M,
=M, 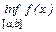 =m. Проведем доказательство для ТВГ:
=m. Проведем доказательство для ТВГ:
M= 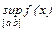 Û 1)
Û 1) 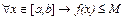 , (8)
, (8) 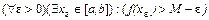 . (9)
. (9)
Полагая e = 1, 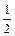 ,
, 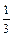 , …,
, …, 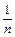 .., в силу условия (9), получим последовательность {xn}: ("nÎN) ® (xnÎ[a,b] Ù f(xn) > M -
.., в силу условия (9), получим последовательность {xn}: ("nÎN) ® (xnÎ[a,b] Ù f(xn) > M - 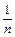 ). (10)
). (10)
Из условий (8), (10) заключаем: ("nÎN)®(M - 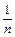 < f(xn) £ M). Это означает, что для сколь угодно больших номеров n значения последовательности {f(xn)} мало отличается от М, т.е.:
< f(xn) £ M). Это означает, что для сколь угодно больших номеров n значения последовательности {f(xn)} мало отличается от М, т.е.: 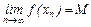 . (11). Аналогично способу доказательства предыдущей теоремы из ограниченной последовательности {xn} можно выделить сходящуюся подпоследовательность:
. (11). Аналогично способу доказательства предыдущей теоремы из ограниченной последовательности {xn} можно выделить сходящуюся подпоследовательность: 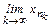 =xÎ[a,b]. В силу непрерывности функции f(x) в точке x, имеем:
=xÎ[a,b]. В силу непрерывности функции f(x) в точке x, имеем: 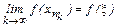 . (12)
. (12)
с другой стороны, 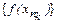 – подпоследовательность сходящейся, согласно равенству (11), последовательности:
– подпоследовательность сходящейся, согласно равенству (11), последовательности: 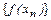 ®M. Поэтому
®M. Поэтому 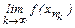 =М. Учитывая единственность предела, из равенства (12) заключаем: f(x)=М=
=М. Учитывая единственность предела, из равенства (12) заключаем: f(x)=М= 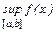 . n
. n
Теорема 3 (Больцано-Коши: о промежуточных значениях). Если функция f(x) непрерывна на [a,b] и f(a)=A, f(b)=B, то ("CÎ[A,B]) ($xÎ[a,b]) : f(x)=C.
gУбедимся, что непрерывная на отрезке функция, принимая какие-либо два значения, также принимает и любое, лежащее между ними, значение.
Пусть для определенности f(a)=A<B=f(b) и A<C<B. Разделим [a,b] точкой х0 пополам. Тогда может быть:
1) f(x0)=C, т.е. искомая точка x=х0 найдена;
2) f(x0)¹C, тогда на концах одного из отрезков функция принимает значения, лежащие по разные стороны от числа С (на левом – меньше С, на правом – больше С).
Обозначим такой отрезок [a1,b1] и снова поделим его пополам, продолжая указанный процесс. В результате: либо через конечное число шагов придем к искомой точке x (f(x)=C); либо получим последовательность вложенных отрезков [an,bn] по длине стремящихся к нулю, для которых выполнено неравенство: f(an) < C <f(bn). (13)
По теореме о вложенных отрезках существует общая точка x всех [an,bn]: an < x < bn Ù bn - an = 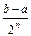 ®0 при n®¥. В силу непрерывности функции f(x) и условий
®0 при n®¥. В силу непрерывности функции f(x) и условий 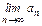 =
= 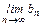 =x имеем равенство:
=x имеем равенство:
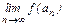 =
= 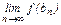 = f(x). (14)
= f(x). (14)
Осуществим предельный переход в неравенстве (13): 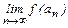 £С£
£С£ 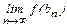 .
.
Учитывая соотношения (14), заключаем, что f(x)=C.n
Теорема 4 (Коши: о нулях непрерывной функции). Если непрерывная функция f(x) на концах [a,b] принимает значения различных знаков, то на [a,b] имеется хотя бы один нуль функции f(x).
Пусть функция f(x) непрерывна на D, т.е. она непрерывна в каждой точке 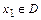 :
:
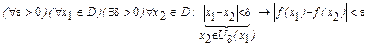 . (15)
. (15)
Непрерывность функции в точке - свойство локальное, так как оно связано с поведением функции в некоторой достаточно малой 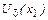 . Величина
. Величина 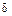 зависит как от
зависит как от 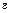 , так и от выбора х1. Покажем, что даже при фиксированном
, так и от выбора х1. Покажем, что даже при фиксированном 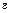 значения
значения 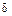 для разных точек
для разных точек 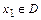 не остаются постоянными.
не остаются постоянными.
 Функция f(x) называется равномерно непрерывной на D, если: ("e>0)($d>0):("x1ÎD)(" x2ÎD):
Функция f(x) называется равномерно непрерывной на D, если: ("e>0)($d>0):("x1ÎD)(" x2ÎD): 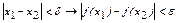 . (16)
. (16)
Теперь число d зависит лишь от e. Свойство равномерной непрерывности (16) является глобальным (касается всего множества D). Неважно в каком месте берутся точки x1, x2ÎD, лишь бы расстояние между ними было меньше d: тогда сразу соответствующие значения функции отличаются по абсолютной величине меньше, чем на e.
Из условия (16) следует (15), поэтому если 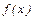 - равномерно непрерывная функция, то она является непрерывной на D (если удалось найти d пригодное для всех значений х, то для каждой точки эта величина также найдена).
- равномерно непрерывная функция, то она является непрерывной на D (если удалось найти d пригодное для всех значений х, то для каждой точки эта величина также найдена).
Теорема (Кантор). Всякая функция, непрерывная на отрезке [a;b], является равномерно непрерывной на нем.
