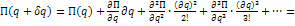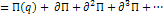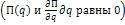Действительное и возможное перемещения при стационарных и нестационарных связях
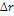 - возможное (виртуальное) перемещение – малое, мысленное перемещение, допускаемое связями с точностью до величин первого порядка малости.
- возможное (виртуальное) перемещение – малое, мысленное перемещение, допускаемое связями с точностью до величин первого порядка малости.
Если в уравнение связи время не входит явно, то такая связь называется стационарной (склерономной):
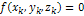
Если в уравнение связи время входит явно, то такая связь называется нестационарной (реономная):
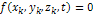
При стационарных связях действительное перемещение совпадает с одним из возможных перемещений. При нестационарной связи действительное перемещение может не совпадать ни с одним из возможных перемещений.
Виртуальные перемещения - возможные перемещения материальных точек системы, допускаемые мгновенно (в момент t) связями, из одной точки по разным траекториям в один и тот же момент времени.
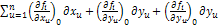 , u=1,2,…,n; i=1,2,…,n
, u=1,2,…,n; i=1,2,…,n
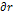 зависит только от связей.
зависит только от связей.
Действительное перемещение материальных точек системы есть возможное перемещение, определяемое связями и уравнениями движения
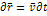
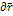 зависит от связей и от сил.
зависит от связей и от сил.
а возможное перемещение только от связей.
10. Устойчивость состояний равновесия: теорема Лагранжа – Дирихле, принцип Торичелли, теорема Ляпунова
По Ляпунову: Устойчивое состояние равновесия системы такое, когда при малом начальном отклонении системы все ее точки будут двигаться не уходя от положения равновесия далее наперед заданного расстояния.
Теорема Лагранжа – Дирихле: При устойчивом равновесии системы ее потенциальная энергия принимает миним. значение
Ограничения: 1) Силы потенциальны
2) Связи голономны, идеальны, стационарны
Принцип Торичелли: При устойчивом равновесии системы ее центр тяжести занимает наинизшее положение.
Ограничения: 1) Силы – силы тяжести
2) Связи идеальны, голономны, стационарны
Теорема Ляпунова:
Равновесие системы неустойчиво, если отсутствие минимума потенциальной энергии системы обнаруживается уже по членам второго порядка в разложении 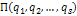 в ряд Тейлора
в ряд Тейлора