Приведение уравнений 4-ой степени

Разделим уравнение (1) на старший коэффициент 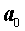. Тогда оно примет вид

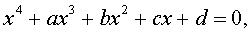(2)

где 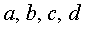- произвольные вещественные числа.

Сделаем в уравнении (2) замену

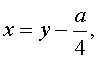(3)

где 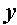- новая переменная.то уравнение принимает вид

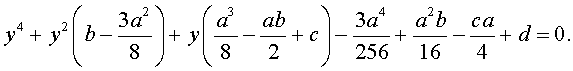(4)

Если ввести обозначения

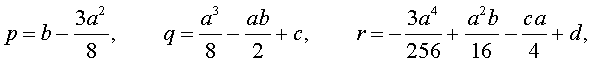
то уравнение (4) примет вид

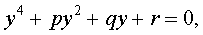(5)

где 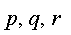- вещественные числа.

Первый этап метода Феррари завершён.

Разложение на множители. Кубическая резольвента

Добавив и вычитая в левой части уравнения (5) выражение

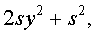
где 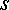- некоторое число, которое мы определим чуть позже, из (5) получим

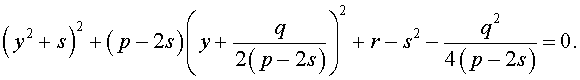(6)

Если теперь выбрать число 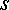так, чтобы оно являлось каким-нибудь решением уравнения

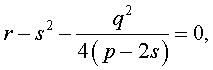	(7)
то уравнение (6) примет вид
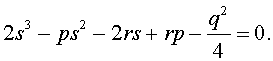	(9)

Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).

Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение

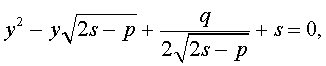(10)

а также квадратное уравнение

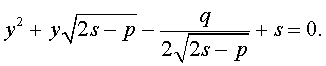(11)

Вывод метода Феррари завершен.

34. многочленом называют сумму одночленов.

Равенство многочленов

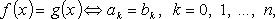
где 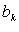- коэффициенты многочлена g(x) ( 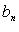- старший коэффициент).

Степенью многочлена называется максимальная из степеней его одночленов, тождественный нуль не имеет степени.

35.Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.

Для того чтобы привести подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.

36. сложения 1. f(x)+g(x)=g(x)+f(x) 2. (f(x)+g(x))+h(x)=f(x)+(g(x))+h(x) 3.a(f(x)+g(x))=af(x)+ag(x) 4. сущест. 0: F(x)+0=f(x) 5)существ. F(x) такое что f(x)+(-f(x))=0

а*в=в*а а*(в*с)=(а*в)*с а*(в+с)=а*в+а*с сущ. 1 а*1=а

37.

38.Говорят, что многочлен P(x) делится на многочлен Q(x), если существует многочлен S(x), такой, что P(x) = Q(x)S(x). Многочлен S(x) называется частным от деления P(x) на Q(x).

Теория делимости многочленов имеет много общего с теорией делимости целых чисел. В частности, выполняются следующие свойства:

1) Если P1(x) и P2(x) делятся на Q(x); то P1(x) + P2(x) и P1(x) - P2(x) делятся на Q(x);

2) Если P(x) делится на Q(x); а T(x) – произвольный многочлен; то P(x)T(x) делится на Q(x);

3) Если P(x) делится на Q(x); а Q(x) делится на H(x); то P(x) делится на H(x):

Доказательство этих свойств ничем не отличается от доказательства соответствующих свойств делимости целых чисел. Отметим еще некоторые простые свойства:

4) Если ненулевой многочлен P(x) делится на Q(x); то deg P(x) ≥ degQ(x);

5) Еесли deg P(x) = degQ(x); то P(x) делится на Q(x) тогда и только тогда, когда эти многочлены пропорциональны:

(Многочлены называются пропорциональными, если один из них получается из другого умножением на число, отличное от 0.)
Действительно, если P(x) делится на Q(x) и deg P(x) = degQ(x), то частное имеет степень 0, т.е. является числом, отличным от 0. Обратное утверждение очевидно.

39. Алгоритм Евклида для многочленов.Алгоритм Евклида позволяет найти наибольший общий делитель двух многочленов, т.е. многочлен наибольшей степени, на который делятся без остатка оба данных многочлена.
Алгоритм основан на том факте, что для любых двух многочленов от одного переменного, f(x) и g(x), существуют такие многочлены q(x) и r(x), называемые соответственно частное и остаток, что

f(x) = g(x)∙q(x) + r(x), (*)

при этом степень остатка меньше степени делителя, многочлена g(x), и, кроме того, по данным многочленам f(x) и g(x) частное и остаток находятся однозначно. Если в равенстве (*) остаток r(x) равен нулевому многочлену (нулю), то говорят, что многочлен f(x) делится на g(x) без остатка.
Алгоритм состоит из последовательного деления с остатком сначала первого данного многочлена, f(x), на второй, g(x):

f(x) = g(x)∙q₁(x) + r₁(x), (1)

затем, если r₁(x) ≠ 0, – второго данного многочлена, g(x), на первый остаток – на многочлен r₁(x):

g(x) = r₁(x)∙q₂(x) + r₂(x), (2)

далее, если r₂(x) ≠ 0, – первого остатка, r₁(x), на второй остаток, r₂(x):

r₁(x) = r₂(x)∙q₃(x) + r₃(x), (3)

затем, если r₃(x) ≠ 0, – второго остатка на третий:

r₂(x) = r₃(x)∙q₄(x) + r₄(x), (4)

и т.д. Поскольку на каждом этапе степень очередного остатка уменьшается, процесс не может продолжаться бесконечно, так что на некотором этапе мы обязательно придем к ситуации, когда очередной, n + 1-й остаток r_{n + 1} равен нулю:

rn–2(x) = rn–1(x)∙ qn(x) + rn(x),	(n)
rn–1(x) = rn(x)∙ qn+1(x) + rn+1(x),	(n+1)
rn+1(x) = 0.	(n+2)

Тогда последний не равный нулю остаток r_n и будет наибольшим общим делителем исходной пары многочленов f(x) и g(x).
Действительно, если в силу равенства (n + 2) подставить 0 вместо r_{n + 1}(x) в равенство (n + 1), затем – полученное равенство r_{n – 1}(x) = r_n(x)∙q_{n + 1}(x) вместо r_{n – 1}(x) – в равенство (n), получится, что r_{n – 2}(x) = r_n(x)∙q_{n + 1}(x) q_n(x) + r_n(x), т.е. r_{n – 2}(x) = r_n(x)( q_{n + 1}(x) q_n(x) + 1), и т.д. В равенстве (2) после подстановки получим, что g(x) = r_n(x)∙Q(x), и, наконец, из равенства (1) – что f(x) = r_n(x)∙S(x), где Q и S – некоторые многочлены. Таким образом, r_n(x) – общий делитель двух исходных многочленов, а то, что он наибольший (т.е. наибольшей возможной степени), следует из процедуры алгоритма.

40. Если наибольший общий делитель двух многочленов не содержит переменную (т.е. является числом), исходные многочлены f(x) и g(x) называются взаимно-простыми.

41.

42. Корень многочлена (не равного тождественно нулю)

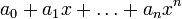
над полем k — элемент 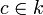, такой что выполняются два следующих равносильных условия:

· данный многочлен делится на многочлен ;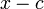

· подстановка элемента c вместо x обращает уравнение

в тождество.

Теорема Безу утверждает, что остаток от деления многочлена 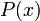на двучлен 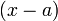равен .

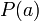Доказательство

Поделим с остатком многочлен 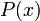на многочлен :

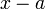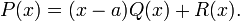
Так как 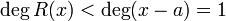, то 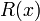— многочлен степени не выше 0. Подставляя <mah>x=a</math>, поскольку 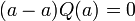, имеем .

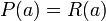43. Задан многочлен :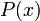

.

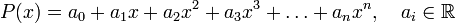Пусть требуется вычислить значение данного многочлена при фиксированном значении 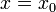. Представим многочлен 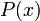в следующем виде:

.

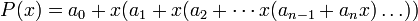Определим следующую последовательность:

…

…

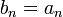
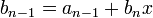
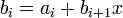
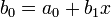
Искомое значение 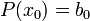. Покажем, что это так.

В полученную форму записи 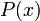подставим 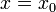и будем вычислять значение выражения, начиная со внутренних скобок. Для этого будем заменять подвыражения через :

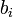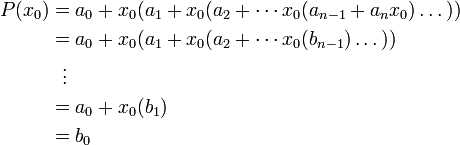
Использование схемы Горнера для деления многочлена на бином

При делении многочле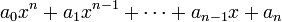на на 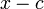получается многочлен 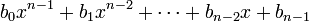с остатком .

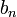При этом коэффициенты результирующего многочлена удовлетворяют рекуррентным соотношениям:

, .

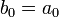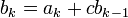Таким же образом можно определить кратность корней (использовать схему Горнера для нового полинома). Так же схему можно использовать для нахождения коэффициентов при разложении полинома по степеням :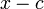

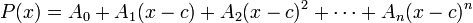
44.Всякий многочлен с любыми комплексными коэффициентами , степень которого не

меньше единицы имеет хотя бы один корень, в общем случае комплексный.

45. Если 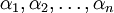— корни многочлена

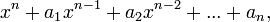
(каждый корень взят соответствующее его кратности число раз), то коэффициенты 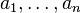выражаются в виде симметрических многочленов от корней, а именно:

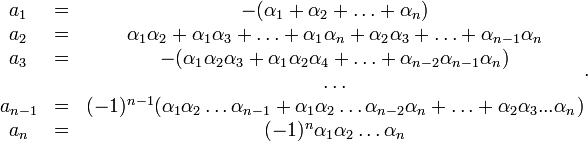
Иначе говоря 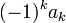равно сумме всех возможных произведений из 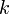корней.

Если старший коэффициент многочлена 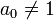, то для применения формулы Виета необходимо предварительно разделить все коэффициенты на (это не влияет на значение корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленен.