VI. Определение абсолютной скорости
И абсолютного ускорения точки. Задание К.5.
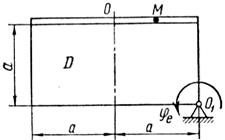
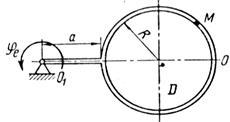
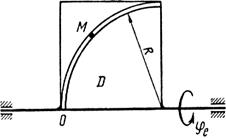
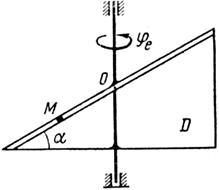
Точка М движется относительно тела D. По заданным уравнениям относительного движения точки М и движения тела D определить для момента времени t = t1 абсолютную скорость и абсолютное ускорение точки М.
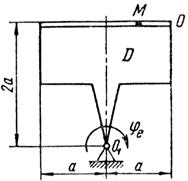
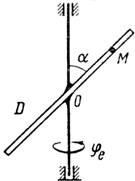
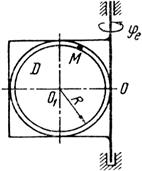
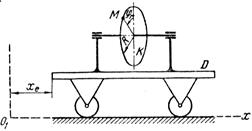
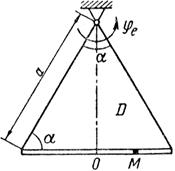
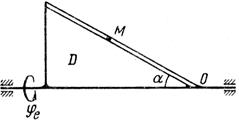
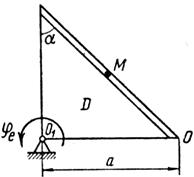
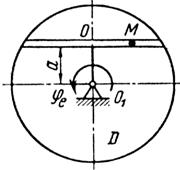
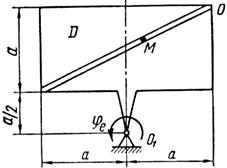
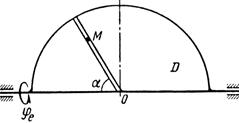
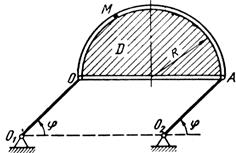
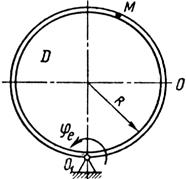
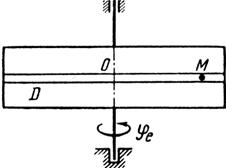
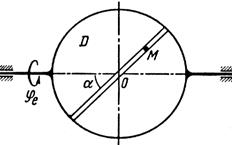
Схемы механизмов показаны на рис. 26-28, а необходимые для расчета данные приведены в табл. 10.
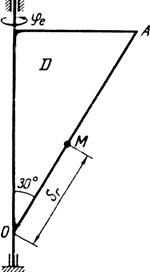
Пример выполнения задания. Дано: схема механизма (рис. 29),
sr = OM = 16 - 8 cos (3πt) см; φс=0,9t2-9t3 рад; t1=2,9 c.
Решение. Будем считать, что в заданный момент времени плоскость чертежа (рис. 29) совпадает с плоскостью треугольника D. Положение точки М на теле D определяется расстоянием sr = ОМ.
При t = 2/9 с
sr = 16 – 8 cos (3π 2/9) = 20,0 см.
Абсолютную скорость точки М найдем как геометрическую сумму относительной и переносной скоростей:
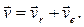
Модуль относительной скорости 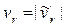 ,
,
где
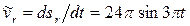 .
.
При t =2/9 с
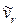 =65,2 см/с; vr = 65,2 см/с.
=65,2 см/с; vr = 65,2 см/с.
Положительный знак у 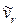 показывает, что вектор
показывает, что вектор 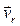 направлен в сторону возрастания sr.
направлен в сторону возрастания sr.
Модуль переносной скорости
| ve=Rωe, | (1) |
где R — радиус окружности L, описываемой той точкой тела, с которой в данный момент совпадает точка М, R = sr sin 30° = 10,0 см; ωe, – модуль угловой скорости тела:
ωе = | 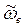 |;
|; 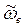 = dφе/dt= 1,8t – 27t2.
= dφе/dt= 1,8t – 27t2.
При t = 2/9 c
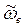 = -0,93 рад/с; ωе = 0,93 рад/с.
= -0,93 рад/с; ωе = 0,93 рад/с.
Отрицательный знак у величины 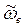 показывает, что вращение треугольника происходит вокруг оси Oz в сторону, обратную направлению отсчета угла φ. Поэтому вектор ωе направлен по оси Oz вниз (рис. 30, а).
показывает, что вращение треугольника происходит вокруг оси Oz в сторону, обратную направлению отсчета угла φ. Поэтому вектор ωе направлен по оси Oz вниз (рис. 30, а).
Таблица 10
| Номер варианта (рис. 26-28) | Уравнение относительного движения точки М OM=sк=sк(t) см | Уравнение движения тела | t1, с | R, см | а, см | α, град | Дополнительные данные | |
| φe=φe(t), рад | xe=xe(t), см | |||||||
| 18sin(πt/4) | 2t3-t2 | — | 2/3 | — | — | |||
| 20sin(πt) | 0,4t2+t | — | 5/3 | — | — | |||
| 6t3 | 2t+ 0,5t2 | — | — | — | ||||
| 10sin(πt/6) | 0,6t2 | — | — | — | ||||
| 40π соз(πt/6) | 3t-0,5t3 | — | — | — | ||||
| — | — | 3t+0,27t3 | 10/3 | — | — | φr=0,15π/t3 | ||
| 20cos(2πt) | 0,5t2 | — | 3/8 | — | ||||
| 6(t+0,5t2) | t3-5t | — | — | — | ||||
| 10(1+sin(2πt) | 4t+1,6t2 | — | 1/8 | — | — | — | ||
| 20π соs(πt/4) | 1,2t-t2 | — | 4/3 | — | ||||
| 25sin(πt/3) | 2t2-0,5t | — | — | — | ||||
| 15πt3/8 | 5t-4t2 | — | — | |||||
| 120πt2 | 8t2-3t | — | 1/3 | — | — | |||
| 3+14sin(πt) | 4t-2t2 | — | 2/3 | — | — | |||
| 3π(t2+t) | 0,2t3+t | — | — | |||||
| 20sin(πt) | t-0,5t2 | — | 1/3 | — | — | |||
| 8t3+2t | 0,5t2 | — | — | 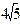 | — | |||
| 10t+t3 | 8t-t2 | — | — | — | ||||
| 6t+4t3 | t+3t2 | — | — | — | ||||
| 30π соs(πt/6) | 6t+t2 | — | — | — | ||||
| 25π(t+t2) | 2t-4t2 | — | 1/2 | — | — | |||
| 10π sin(πt/4) | 4t-0,2t2 | — | 1/3 | — | — | |||
| 6πt2 | — | — | — | — | φ=5πt3/6; О1О=О2А=30 см | |||
| 75π(0,1t+0,3t3) | 2t-0,3t2 | — | — | — | ||||
| 15sin(π/t3) | 10t-0,1t2 | — | — | — | — | |||
| 8cos(π/t2) | -2πt2 | — | 3/2 | — | — | |||
| — | — | 50t2 | — | — | φr=5πt3/48 | |||
| 2,5πt2 | 2t3-5t | — | — | — | ||||
| 5πt3/4 | — | — | — | — | φ=πt3/8; О1О=О2А=40 см | |||
| 4πt2 | — | t3+4t | — | — |
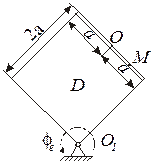
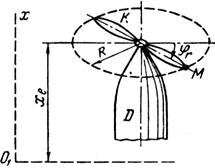
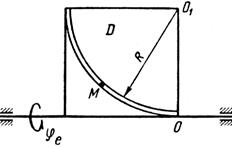
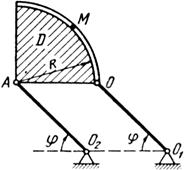
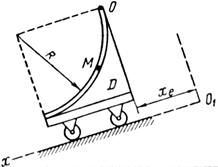
Примечания. Для каждого варианта положение точки M на схеме соответствует положительному значению sr; в вариантах 5, 10, 12, 13, 20—24, 28 — 30 OM= sr —дуга окружности; на схемах 5, 10, 12, 21, 24 ОМ — дуга, соответствующая меньшему центральному- углу. Относительное движение точки M в вариантах 6 и 27 и движение тела D в вариантах 23 и 29 определяются уравнениями, приведенными в последнем столбце табл. 10.
 |  | ||
 |  | ||
 |  | ||
 |  | ||
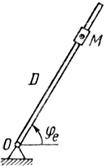 | 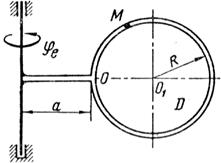 | ||
| Рис. 26. |
 |  | ||
 |  | ||
 |  | ||
 |  | ||
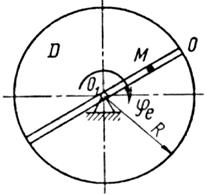 | 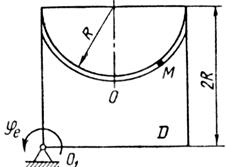 | ||
| Рис. 27. |
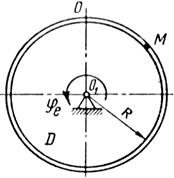 | 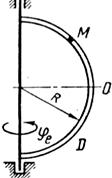 | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
| Рис. 28. |
 | Модуль переносной скорости, по формуле (1), ve = 9,3 см/с. Вектор 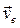 направлен по касательной к окружности L в сторону вращения тела. Так как направлен по касательной к окружности L в сторону вращения тела. Так как 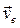 и и 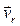 взаимно перпендикулярны, модуль абсолютной скорости точки М взаимно перпендикулярны, модуль абсолютной скорости точки М 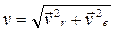 , v = 65,9 см/с. Абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений: , v = 65,9 см/с. Абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений: 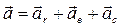 , или в развернутом виде , или в развернутом виде 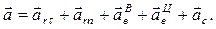 |
| Рис. 29 |
Модуль относительного касательного ускорения
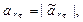 где
где 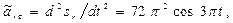
При t = 2/9 c. 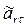 = –355 см/с2;
= –355 см/с2; 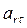 = 355 см/с2.
= 355 см/с2.
Отрицательный 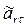 показывает, что вектор
показывает, что вектор 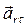 направлен в сторону отрицательных значений sr. Знаки
направлен в сторону отрицательных значений sr. Знаки 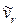 и
и 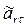 одинаковы; следовательно, относительное движение точки М ускоренное.
одинаковы; следовательно, относительное движение точки М ускоренное.
