Рівняння прямої з кутовим коефіцієнтом
Розглянемо рівняння (1) із 3.2

Позначивши  , отримаємо
, отримаємо

рівняння пучка прямих, або рівняння прямої, що проходить через точку 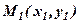 у заданому напрямку. Геометричний зміст коефіцієнта
у заданому напрямку. Геометричний зміст коефіцієнта  зрозумілий з рис. 6.
зрозумілий з рис. 6.
В  , де
, де 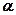 – найменший кут, на який потрібно повернути додатний напрямок осі
– найменший кут, на який потрібно повернути додатний напрямок осі 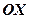 навколо спільної точки
навколо спільної точки  до суміщення її з прямою
до суміщення її з прямою  . Очевидно, що якщо кут
. Очевидно, що якщо кут 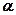 – гострий, то
– гострий, то  ; якщо ж
; якщо ж 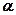 – тупий кут, то
– тупий кут, то  .
.
Розкриємо дужки в (5) і спростимо його

де  . Співвідношення (6) – рівняння прямої з кутовим коефіцієнтом. При
. Співвідношення (6) – рівняння прямої з кутовим коефіцієнтом. При  – відрізок, який відтинає пряма на осі
– відрізок, який відтинає пряма на осі 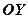 (див. рис.6).
(див. рис.6).
Звернемо увагу, що для переходу від загального рівняння прямої 
 до рівняння з кутовим коефіцієнтом необхідно перше розв’язати відносно
до рівняння з кутовим коефіцієнтом необхідно перше розв’язати відносно 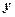
 |
Рис.6

де позначено  . Якщо ж
. Якщо ж  , то із дослідження загального рівняння вже відомо, що така пряма перпендикулярна осі
, то із дослідження загального рівняння вже відомо, що така пряма перпендикулярна осі 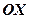 .
.
