Вопрос 22.3. Остаточный член формулы Тейлора в форме Лагранжа

Теорема Пеано утверждает, что остаточный член формулы Тейлора имеет n порядок малости, но не определяет величину остаточного члена. На этот вопрос отвечает теорема Лагранжа.

Теорема 22.2. Пусть функция имеет производную n‑1 ‑го порядка в окрестности точки a. Тогда справедлива формула Тейлора n‑го порядка

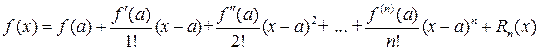
с остаточным членом в форме Лагранжа

,

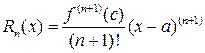где c некоторое число, заключенное между a и x.

Доказательство. Пусть 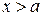. Если , 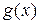непрерывны на отрезке 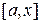и дифференцируемы внутри отрезка, причем 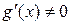, то по теореме Коши

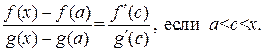
Положим 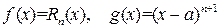, тогда по теореме Коши

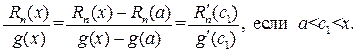
Далее

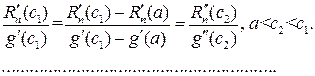
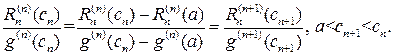
Отсюда

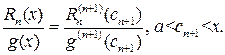
Так как 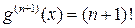и 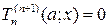, то, положив 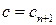, получим

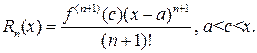
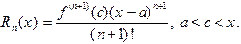
Конец доказательства.

Пример 22.1. Вычислить функцию 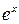при с точностью .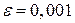

Разложим функцию 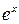по формуле Маклорена с остаточным членом в форме Лагранжа

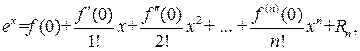
где

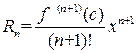
Так как верно равенств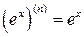о , то

,

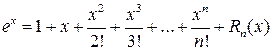где

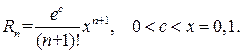
Так как справедливы неравенства 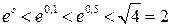, то для остаточного члена получаем оценку

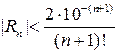
откуда получаем

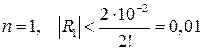
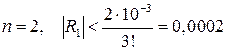
Тогда

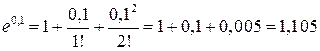
с точностью .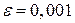

Конец примера.

ЛЕКЦИЯ № 23. РАЗЛОЖЕНИЕ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ ПО ФОРМУЛЕ ТЕЙЛОРА.

Волрос 23.1. Разложение некоторых элементарных функций по формуле Тейлора.

Рассмотрим разложение некоторых элементарных функций по формуле Тейлора в точке 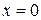(формула Маклорена).

1) .

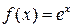Разложение этой функции было получено в лекции № 22. Приведем его, поэтому, без пояснений

.

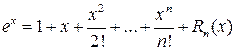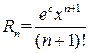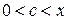Здесь остаточный член в форме Лагранжа равен , где или .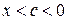

2) .

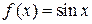Вычислим производные этой функции:

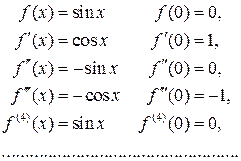
Отсюда получаем 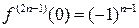, тогда по формуле Маклорена найдем

,

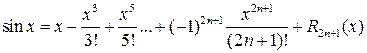где 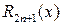‑ остаточный член в форме Лагранжа. Для него можно получить оценку

.

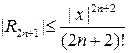Пример 23.1. Вычислить 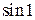с точностью .

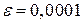Оценим остаточный член

,

,

.

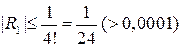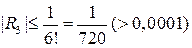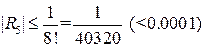получим

.

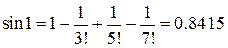Конец примера.

3)

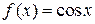
Вычислим производные этой функции:

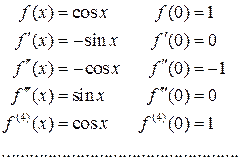
Отсюда получаем 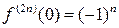, тогда по формуле Маклорена найдем

,

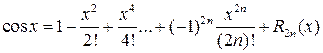где 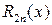‑ остаточный член в форме Лагранжа. Для него можно получить оценку

.

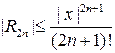Пример 23.2. Вычислить 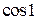с точностью .

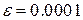Оценим остаточный член

,

,

,

.

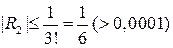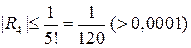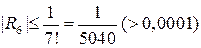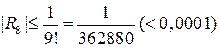получим

.

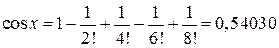Конец примера.

4)

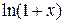
Вычислим производные этой функции:

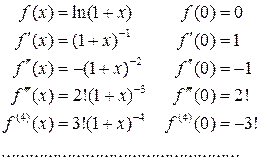
Отсюда получаем 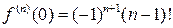, тогда по формуле Маклорена найдем

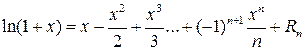
где 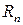‑ остаточный член в форме Лагранжа. Для него можно получить оценку

.

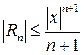Пример 23.3. Вычислить 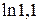с точностью .

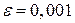. Оценим остаточный член

,

.

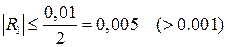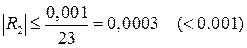получим .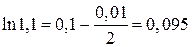

Конец примера.

5)

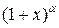
Вычислим производные этой функции:

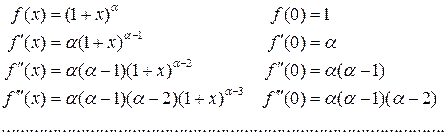
Отсюда получаем 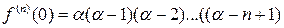, тогда по формуле Маклорена найдем

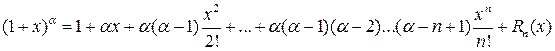
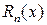‑ остаточный член в форме Лагранжа. Для него можно получить оценку :

.

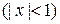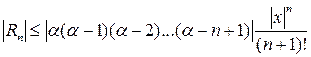Пример 23.4. Вычислить 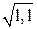с точностью .

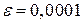Оценим остаточный член

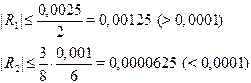
Тогда получим .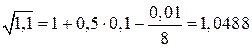

Конец примера.