Где и – коэффициенты парной и межфакторной корреляции

Коэффициенты «чистой» регрессии 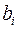связаны со стандартизованными коэффициентами регрессии 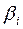следующим образом:

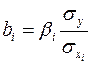. (2.6)

Поэтому можно переходить от уравнения регрессии в стандартизованном масштабе (2.4) к уравнению регрессии в натуральном масштабе переменных (2.1), при этом параметр определяется как .

Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов – из модели исключаются факторы с наименьшим значением .

На основе линейного уравнения множественной регрессии

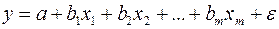(2.7)

могут быть найдены частные уравнения регрессии:

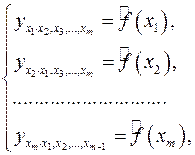(2.8)

т.е. уравнения регрессии, которые связывают результативный признак с соответствующим фактором 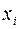при закреплении остальных факторов на среднем уровне. В развернутом виде систему (2.8) можно переписать в виде:

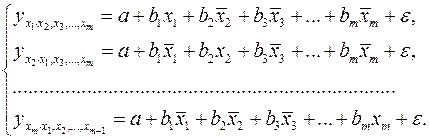
При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т.е. имеем

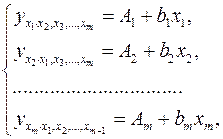(2.9)

где

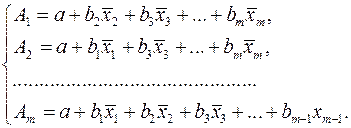
В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности:

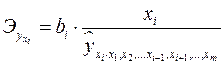, (2.10)

Где – коэффициент регрессии для фактора в уравнении множественной регрессии, – частное уравнение регрессии.

Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности:

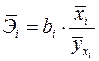, (2.11)

Которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.

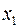Рассмотрим пример[4] (для сокращения объема вычислений ограничимся только десятью наблюдениями). Пусть имеются следующие данные (условные) о сменной добыче угля на одного рабочего (т), мощности пласта (м) и уровне механизации работ 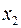(%), характеризующие процесс добычи угля в 10 шахтах.

Таблица 2.2

№

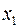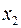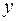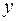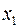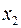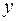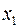Предполагая, что между переменными , , существует линейная корреляционная зависимость, найдем уравнение регрессии по и .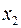

Для удобства дальнейших вычислений составляем таблицу ( ):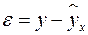

Таблица 2.3

№
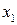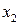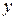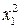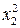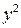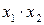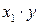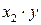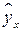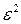										5,13	0,016
										8,79	1,464
										9,64	0,127
										5,98	1,038
										5,86	0,741
										6,23	0,052
										6,35	0,121
										5,61	0,377
										5,13	0,762
										9,28	1,631
Сумма											6,329
Среднее значение	9,4	6,3	6,8	90,8	41,7	49,6	60,3	66,4	44,5	–	–
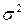	2,44	2,01	3,36	–	–	–	–	–	–	–	–
	1,56	1,42	1,83	–	–	–	–	–	–	–	–

Для нахождения параметров уравнения регрессии в данном случае необходимо решить следующую систему нормальных уравнений:

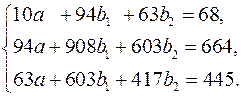
Откуда получаем, что 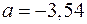, , 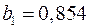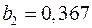. Т.е. получили следующее уравнение множественной регрессии:

.

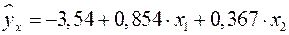Оно показывает, что при увеличении только мощности пласта 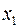(при неизменном 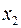) на 1 м добыча угля на одного рабочего 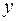увеличится в среднем на 0,854 т, а при увеличении только уровня механизации работ 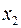(при неизменном 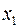) на 1% – в среднем на 0,367 т.

Найдем уравнение множественной регрессии в стандартизованном масштабе:

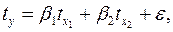
при этом стандартизованные коэффициенты регрессии будут

,

.

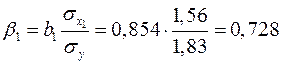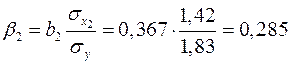Т.е. уравнение будет выглядеть следующим образом:

.

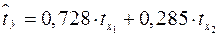Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что мощность пласта оказывает большее влияние на сменную добычу угля, чем уровень механизации работ.

Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности (2.11):

.

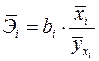Вычисляем:

, .

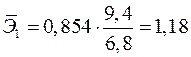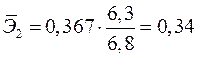Т.е. увеличение только мощности пласта (от своего среднего значения) или только уровня механизации работ на 1% увеличивает в среднем сменную добычу угля на 1,18% или 0,34% соответственно. Таким образом, подтверждается большее влияние на результат 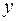фактора 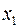, чем фактора .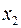