Дифференциальные уравнения 5 страница
В задачах 1.11-1.15 даны статистические ряды. Выполните те же задания, что и в задаче 1.10.
1.11.Таблица 19.
| Гра ницы интерв. | 85-105 | 105-125 | 125-145 | 145-165 | 165-185 | 185-205 | 205-225 |
| Частота |
1.12. Таблица 20.
| Границы интерв. | 60-64 | 64-68 | 68-72 | 72-76 | 76-80 | 80-84 |
| Частота |
1.13. Таблица 21.
| Границы интерв. | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 |
| Частота |
1.14.Таблица 22.
| Границы интерв. | 10-14 | 14-18 | 18-22 | 22-26 | 26-30 | 30-34 |
| Частота |
1.15.Таблица 23.
| Границы интерв. | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 | 12-14 |
| Частота |
Задача 2.
Случайная величина распределена по нормальному закону с параметром « 
» (сигма). Сделана выборка объема n. Найти с надежностью 
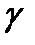доверительный интервал для неизвестного параметра а, если:
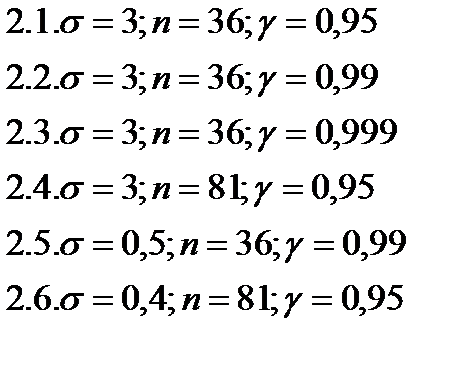
случайная величина распределена по нормальному закону с параметром « ». Найдите минимальный объем выброски n, чтобы с надежностью « 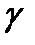» и точностью « 
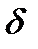» выполнялась равенство Х=а, если:
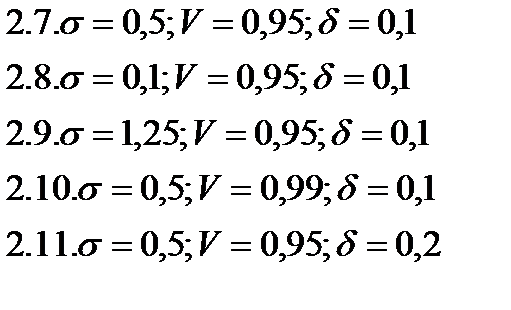
2.12 Из нормально распределенной генеральной совокупности сделана выборка:
Таблица 24.
| -1,90 | 1,37 | -0,89 | -0,13 | 0,15 | -1,79 | -0,96 | 1,55 | 0,40 | 0,69 |
| -0,90 | 0,15 | 0,90 | ,082 | 1,53 | -0,34 | 0,98 | -1,38 | 1,48 | -0,65 |
| 1,10 | 0,30 | -0,13 | -1,90 | -0,32 | -0,42 | 0,77 | 0,08 | 0.17 | 0,87 |
Найдите с надежностью 0,9 доверительный интервал для математического ожидания, считая дисперсию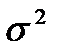 
равной единице.
С надежностью « 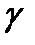» найдите доверительный интервал для математического ожидания нормально распределенной генеральной совокупности с неизвестной дисперсией по выборке объема «n», если:
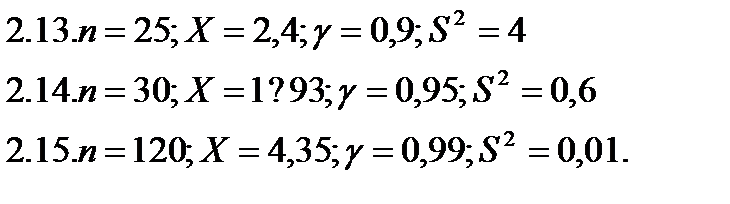
Задача 3.
3.1Для изучения мощности тракторных парков было обследовано 250 парков из 2500, отобранных по схеме собственно-случайной выборки. Их распределение по мощности тракторных парков дано в таблице 25:
Таблица 25.
| Мощности, тыс.л.с | 0,6-0,1 | 1,0-1,4 | 1,4-1 | 1,8-2,2 | 2,2-2,6 | 2,6-3,0 | 3,0-3,4 | итого |
| Число парков |
Найти границы, в которых с вероятностью 0,9876 заключена средняя мощность тракторного парка для всей совокупности парков, если выборка: а) повторная; б) бесповторная.
3.2. Испытывалась чувствительность второго канала 100 телевизоров из партии 2000 шт., изготовленных одним заводом. Получены следующие данные:
Таблица 26.
| Чувствительность канала МТВ | 475-525 | 525-575 | 575-625 | 625-675 | 675-725 | итого |
| Число телевизоров |
Определить вероятность того, что средняя чувствительность второго канала во всей партии телевизоров отличается от полученной средней чувствительности телевизоров в выборке не более чем на 10 МВТ по абсолютной величине. Задачу решить для повторной и бесповторной выборок.
3.3. Чтобы установить содержание золы на очень большой партии каменного угля, было взято 500 проб. Результаты анализа приведены в таблице 27:
| Содержание золы,% | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 | 17-19 | 19-21 | итого | |
| Число проб |
Таблица 27.
3.4.В детском спорткомплексе занимаются 2000 школьников. Для определения их среднего возраста случайным бесповторным отбором взята информация у 100 детей. Результаты выборки показаны в таблице 28:
Таблица 28.
| Возраст, лет | 6-8 | 8-10 | 10-12 | 12-14 | 14-16 | 16-18 | итого |
| Колич опрош. |
Найти: а) границы, в которых с вероятностью 0,97 заключен средний возраст школьников, посещающих этот спорткомплекс; б) вероятность того, что доля школьников, старше 12 лет, среди всех посетителей отличается от выборочной доли таких школьников не более чем на 0,12 (по абсолютной величине).
3,5. Для определения средней мощности моторов по схеме бесповторного случайного отбора было обследовано 100 моторов из 1000, имеющихся на заводе, результаты которого приведены в таблице 29:
Таблица 29.
| Мощность моторов, кВт | 3,7-3,8 | 3,8-3,9 | 3,9-4,0 | 4,0-4,1 | 4,1-4,2 | 4,2-4,3 | итого |
| Колич. моторов |
Найти: а) вероятность того, что средняя мощность всех моторов отличается от средней выборочной не более чем на 0,01 по абсолютной величине; б) границы, в которых с вероятностью 0,8064 заключена средняя мощность моторов во всей партии.
3,6. Из партии, содержащей 4000 деталей, было отобрано по схеме собственно случайной бесповторной выборки 400 деталей. Распределение этих деталей по длине дано в таблице 30:
Таблица 30.
| Длина, мм | 3,2-3,3 | 3,3-3,4 | 3,4-3,5 | 3,5-3,6 | 3,6-3,7 | итого |
| Число деталей |
Требуется найти: а) границы, в которых с вероятностью 0,9973 заключена средняя длина деталей во всей партии; б) вероятность того, что доля деталей во всей партии, длина которых составляет от 3,4 до 3,6 мм, отличается от доли таких деталей в выборке не более чем на 0,01 по абсолютной величине.
3.7. Данные о продолжительности 150 телефонных разговоров, отобранных по схеме собственно случайной повторной выборки, представлены в таблице 31:
Таблица 31.
| Продолжительность разговора, мин | 1,5-2,5 | 2,5-3,5 | 3,5-4,5 | 4,5-5,5 | 5,5-6,5 | 6,5-7,5 | 7,5-8,5 | 8,609,5 | 9,5-10,5 | итого |
| Число разговоров |
Необходимо: 1) найти границы, в которых с вероятностью 0.9973 заключена средняя продолжительность телефонного разговора в генеральной совокупности; 2) найти вероятность того, что доля телефонных разговоров, продолжительность которых превышает 8,5 мин. По данным выборки, отличается от доли таких разговоров в генеральной совокупности не более чем на 0,05 по абсолютной величине.
3.8. Для анализа выполнения плана реализации услун в 5000 предприятиях бытового обслуживания в регионе было проверено по схеме случайной бесповторной выборки 200 предприятий. Результаты прверки даны в таблице 32:
Таблица 32.
| Выполнение плана, % | 90-93 | 93-96 | 96-99 | 99-102 | 102-105 | 105-108 | итого |
| Число предприятий |
Найти: а)вероятность того, что средний процент выполнения плана всеми предприятиями отличается от среднего выборочного не более чем на 0,5% по абсолютной величине; б) границы доли предприятий, которые выполнили план не более чем на 99% с вероятностью 0,9973.
3.9. Для определения средней стоимости пошива одной вещи в ателье из 10000 заказов по схеме собственно случайной бесповторной выборки было отобрано 500 квитанций, распределение суммы заказа на которых дано в таблице 33:
Таблица 33.
| Стоимость заказа, руб. | 0-100 | 100-200 | 200-300 | 300-400 | 400-500 | 500-600 | Более 600 | итого |
| Число квитанций |
Найти: а) границы, в которых с вероятностью 0,899 заключена средняя стоимость заказа во всей партии; б) вероятность того, что доля всех заказов стоимостью от 200 до 500 руб. отличается от доли их в выборке не более чем на 0,05 (по абсолютной величине).
3.10. По схеме собственно случайной беспаовторной выборки было отобрано 100 студенток из 1500 и получены следующие данные о их росте:
Таблица 34.
| Рост, см | 154-158 | 158-162 | 162-166 | 166-167 | 170-174 | 174-178 | мтого |
| Число студенток |
Найти: 1) границы, в которых с вероятностью 0,95 заключен средний рост студенток во всей совокупности; 2) вероятность того, что доля студенток, рост которых не менее 170 см во всей совокупности, отличается от выборочной доли таких студенток не более чем на 0,05.
3.11Из партии в 1 млн. шт. мелкокалиберных патронов путем случайного отбора взято для определения дальнобойности боя 1000шт.
Результаты испытаний представлены в таблице
Таблица 35
| Дальность боя, м | Итого | ||||||
| Число патронов. шт |
С вероятностью 0,954 определите среднюю дальность боя по выборке. Ошибку выборки и возможные пределы средней дальности бля для всей партии патронов.
3.12 В процессе подготовки выборочного обследования качества импортируемых изделий была проведена пробная проверка 8 ящиков для сбора данных о вариации их веса.
Таблица 36.
| № ящика | ||||||||
| Средний вес коробки, г |
Сколько ящиков с кондитерскими изделиями необходимо отобрать для проверки качества в порядке бесповторного отбора, чтобы с вероятностью 0,997 ошибка выборки не превышала 20 г. Если генеральная совокупность включает 1000 равных по величине серий?
3.13 В порядке механической выборки обследован возраст 100 студентов вуза из обшего числа 2000 человек. Результаты обработки материалов наблюдения приведены в таблице:
Таблица 37.
| Возраст, лет | |||||||
| Число студентов |
Установите: а) средний возраст студентов вуза по выборке;
б) велечину ошибки при определении возраста студентов на основе выборки; в) вероятные пределы колебания возраста для всех студентов про вероятности 0,997.
3.14 Качество партии молочных продуктов, состоящей из 5000 пакетов. Упакованных в ящики по 20 пакетов, проверялось с помощью 2%-ной серийной бесповторной выборки.
Таблица 38.
| Показатели | |||||
| Средний срок хранения , дней | 2,5 | 3,5 | |||
| Удельный вес продуктов со сроком хранения не менее 3 дней | 0,88 | 0,76 | 0,92 | 0,70 | 0,98 |
С вероятностью 0,997 определите: а) пределы среднего срока хранения молочных продуктов во всей партии; б) пределы доли молочных продуктов со сроком хранения не менее 3 дней.
3.15 При обследовании семейных бюджетов населения города была организована 10%-ная типическая пропорциональная выборка.
Таблица 39.
| Группы населения по семейному положению | Объем выборки | Доля расходов на оплату жилья % |
| Одинокие | ||
| Семейные |
С вероятностью 0,683 установите границы доли расходов на оплату жилья населением города.
Задача 4.
4.1. Используя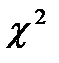 
- критерий Пирсона на основе выборочных данных задачи №3 при уровне значимости 
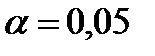проверить гипотезу о том, что случайная Х – мощность тракторного парка – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
4.2. Используя 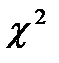- критерий Пирсона на основе выборочных данных задачи №3 при значимости 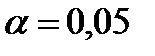проверить гипотезу о том, что случайная Х – средняя чувствительность второго канала - распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
4.3. Используя 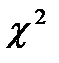- критерий Пирсона на основе выборочных данных задачи №3 при уровне значимости 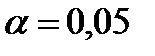проверить гипотезу о том, что случайная Х – процент вольности каменного угля – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую
4.4. Используя 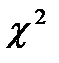- критерий Пирсона на основе выборочных данных задачи №3 при уровне значимости 
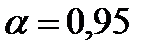проверить гипотезу о том, что случайная Х – возраст детей в спорткомплексе – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
4.5. Используя 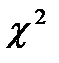- критерий Пирсона на основе выборочных данных задачи №3 при уровне значимости 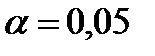проверить гипотезу о том, что случайная Х (средняя мощность мотора) распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую).
4.6. Используя 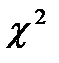- критерий Пирсона на основе выборочных данных задачи №3 при уровне значимости 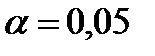проверить гипотезу о том, что случайная Х – длина детали – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
4.7. Используя 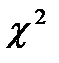- критерий Пирсона на основе выборочных данных задачи №3 при уровне значимости 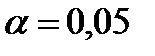проверить гипотезу о том, что случайная Х – продолжительность телефонного разговора мощность тракторного парка – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
4.8. Используя 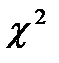- критерий Пирсона на основе выборочных данных задачи №3 при уровне значимости 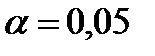проверить гипотезу о том, что случайная Х – процент выполняемого плана – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
4.9. Используя 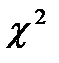- критерий Пирсона на основе выборочных данных задачи №3 при уровне значимости 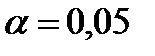проверить гипотезу о том, что случайная Х – стоимость заказа в ателье – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
4.10. Используя 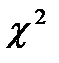- критерий Пирсона на основе выборочных данных задачи №3 при уровне значимости 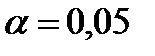проверить гипотезу о том, что случайная Х – рост студентки – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
4.11 Используя критерии Пирсона, при уровне значимости 0,05 проверить согласуется ли гипотеза о нормальном распределении генеральной совокупности Х с эмпирическим распределением выборки объем n=200
| X | |||||||||
| N |
4.12 Используя метод Пирсона, при уровне значимости 0,05 проверять согласуется ли гипотеза о нормальном распределении генеральной совокупности Х с эмпирическим распределением выборки объем n=200
| X | 0,3 | 0,5 | 0,7 | 0,9 | 1,1 | 1,3 | 1,5 | 1,7 | 1,9 | 2,1 | 2,3 |
| N |
4.13 Используя метод Пирсона, при уровне значимости 0,05 проверять согласуется ли гипотеза о нормальном распределении генеральной совокупности Х с эмпирическим распределением выборки объем n=200
| X | |||||||||
| N |
4.14 Используя метод Пирсона, при уровне значимости 0,05 проверять согласуется ли гипотеза о нормальном распределении генеральной совокупности Х с эмпирическим распределением выборки объем n=200
| X | |||||
| N |
4.15 Используя метод Пирсона, при уровне значимости 0,05 проверять согласуется ли гипотеза о нормальном распределении генеральной совокупности Х с эмпирическим распределением выборки объем n=200
| X | |||||||
| N |
Задача 5.
Предполагая, что во всех случаях между переменными х и у существует линейная корреляционная зависимость, требуется: а) вычислить коэффициенты регрессии; б) вычислить коэффициент корреляции и решить вопрос о тесноте связи между рассматриваемыми переменными величинами; в) составить уравнения прямых регрессии.
Получены следующие распределения:
5.1. Прямоугольных плиток по длине х (см) и по массе у (кг)
Таблица 40.
| х/у | Итого | |||||
| - | ||||||
| - | - | |||||
| - | ||||||
| - | - | |||||
| - | - | |||||
| Итого |
5.2. Заводов по основным фондам х и по годовой продукции у (млн.руб.)
Таблица 41.
| х/у | Итого | |||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | |||||
| - | ||||||
| - | - | |||||
| Итого |
5.3. Растений по массе каждого из них х и по массе семян у (г)
Таблица 42.
| х/у | Итого | |||||
| - | - | - | ||||
| - | - | |||||
| - | ||||||
| - | - | |||||
| - | - | - | ||||
| Итого |
5.4. Предприятие по объему продукции х и по ее себестоимости . (руб.)
Таблица 43.
| х/у | 2,5 | 3,5 | Итого | |||
| - | - | - | ||||
| - | - | |||||
| - | - | |||||
| - | ||||||
| - | - | - | ||||
| Итого |
5.5. Проб руды по содержанию окиси железа х и закиси железа у (%).
Таблица 44.
| х/у | Итого | ||||||
| - | - | - | - | ||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | - | - | ||||
| - | - | - | - | ||||
| - | - | - | - | - | |||
| Итого |
5.6. Однотипных предприятий по основным фондам х (млн.руб)и себестоимости единицы продукции у (руб.)
Таблица 45.
| х/у | 1,25 | 1,5 | 1,75 | 2,25 | Итого | |
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | - | ||||
| Итого |
5.7.
Таблица 46.