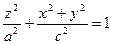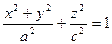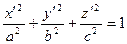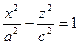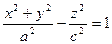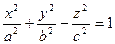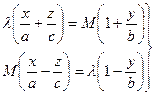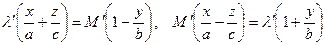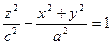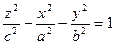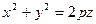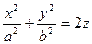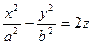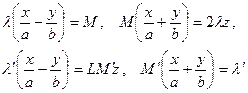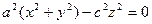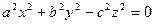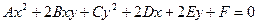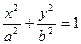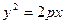Цилиндрические и сферические координаты

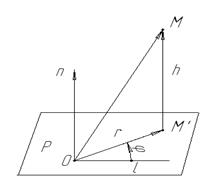
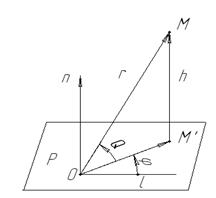
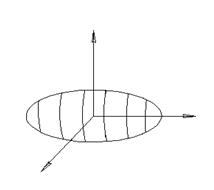
В пространстве обобщением полярных систем координат являются цилиндрические и сферические системы координат. И для тех, и для других фигура, относительно которой определяется положение точки, состоит из точки 0, луча l, исходящего из 0 и вектора n, неравному по длине единице и перпендикулярному к l. Через точку 0 можем провести плоскость P, перпендикулярную вектору n.

Пусть дана некоторая точка М. Опустим из ее перпендикуляр на плоскость P.

Цилиндрические координаты точки M(r,j, h), числа r,j - полярные координаты, точка 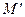по отношению к полуоси 0 и полярной оси l, а h – компонента 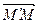по вектору n. Она определена, так как эти векторы коллиниарны.

Сферические координаты точки (r,j, Q). Они определяются так: 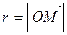; как и для цилиндрических координат j - углов вектора, 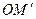с лучом l; и Q – угол с плоскостью P.

11. Поверхности второго порядка:

• эллипсоид;

Рассмотрим поверхности, которые получаются при вращении эллипс вокруг его осей симметрии. Направив вектор l₃ сначала вдоль малой оси эллипса, а затем вдоль большой оси, мы получим уравнение эллипса в следующих видах: 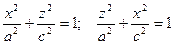, (здесь через с обозначена малая полуось эллипса).

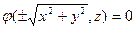В силу формулы уравнения соответствующих поверхностей вращения будут :

(1) и (2).

Поверхности (1) и (2) называются сжатым и вытянутым эллипсоидами вращения.

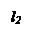
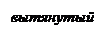
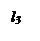
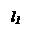
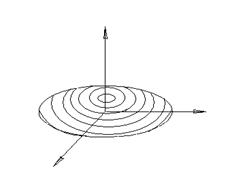
Каждую точку M(x; y; z) эллипсоиде вращения (1) сдвинем на плоскости g (координаты плоскости, проходят через l₁ и l₃) та, чтобы расстояние от точки до этой плоскости уменьшилось в постоянном для всех отношений 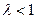. После сдвига М совпадет с 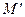, координаты которой определяются равенствами 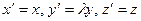. Т.о., все точки эллипсоида вращения (1) переходят в точки поверхности с уравнением:

(3), где .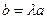

Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение (3), называется эллипсоидом.

Если случайно окажется b = c, получим снова эллипсоид вращения, но уже вытянутый. Эллипсоид, так же как и эллипсоид вращения, из которого он получен, представляет собой замкнутую ограниченную поверхность. Из уравнения (3) видно, что (0; 0; 0) – центр симметрии для эллипсоида, а координатные плоскости – его плоскости симметрии.

Эллипсоид получается из эллипсоида вращения сжатием так же, как эллипс получается сжатием окружности. Сжатием сферы 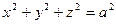можно получить эллипсоид вращения (1). Для того, чтобы из сферы получить вытянутый эллипсоид, нужно сделать аналогичное преобразование, но 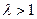- растяжение.

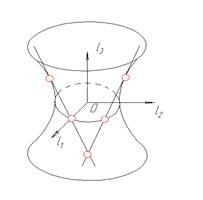
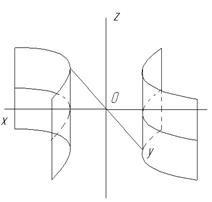
• однополостный гиперболоид;

Однополостный гиперболоид вращения – это поверхность вращения гиперболы вокруг той ее оси, которая ее не пересекает.

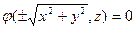По формуле получаем уравнение однополосного гиперболоида:

(4).

В результате сжатия этой поверхности получаем поверхность с уравнением:

(5).

Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение (5), называемая однополостным гиперболоидом.

Свойство однополостного гиперболоида – наличие у него прямолинейных образующих. Так называются прямые линии, всеми своими точками лежащие на поверхности.

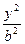Через каждую точку однополосного гиперболоида проходит две прямолинейные образующие, уравнение которых можно получить следующим образом. Перенесем член в правую часть уравнения (5) и разложим обе части равенства на множители: .

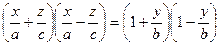Рассмотрим прямую линию с уравнениями (6), где

l и М – некоторые числа одновременно неравные 0. Координаты каждой точки прямой удовлетворяют обоим уравнениям, следовательно и их произведению – уравнению (5). Поэтому все точки прямой (5) лежат на однополостном гиперболоиде

Подставляя координаты точки лежащей на однополостном гиперболоиде, в одном из уравнений (5) и в одно из уравнений (6), найдем отношения параметров l, М и , которые соответствуют прямолинейным образующим, проходящим через эту точку.

Если вместе с гиперболой вращать и ее асимптоты, то они опишут прямой круговой конус, называемый асимптотическим конусом гиперболоида вращения.

• двуполостный гиперболоид;

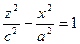Двуполостный гиперболоид вращения – это поверхность вращения гиперболы: вокруг той оси, которая ее пересекает. По формуле 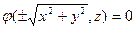получаем уравнение двуполостного гиперболоида вращения:

(8).

В результате сжатия этой поверхности получается поверхность с уравнением

(9).

Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение вида (9), называется двуполостным гиперболоидом.

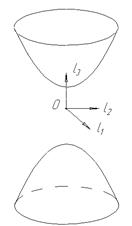
Двум ветвям гиперболы соответствуют здесь две не связанные между собой части, поверхности, в то время как, например, при построении однополосного гиперболоида вращения каждая ветвь гиперболы описывает всю поверхность.

• эллиптический параболоид;

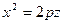При вращении параболы вокруг ее оси симметрии мы получаем поверхность с уравнением

(10),

называемую параболоидом вращения в поверхность с уравнением

(11).

Поверхность, которая имеет такое уравнение в некоторой декартовой прямоугольной системе координат, называется эллиптическим параболоидом .Сечение этой поверхности плоскостями z = a при а > 0 представляют собой эллипсы 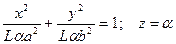, а сечения плоскостями, параллельны другим координатным плоскостям, например плоскостями 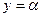, - параболы .

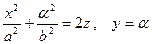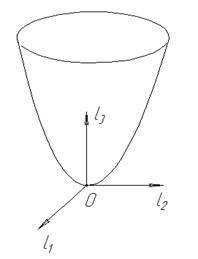
• гиперболический параболоид;

(12)

Поверхность, которая имеет в некоторой декартовой прямоугольной системе координат уравнение вида (12), называется гиперболическим параболоидом.

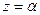Сечение гиперболического параболоида плоскостью представляют собой гиперболу, которая в этой плоскости имеет уравнение: 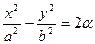в системе координат 0^*, l₁, l₂ с началом в точке (0, 0, a). Для больших + - ных a полуоси гиперболы 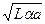и 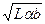велики и уменьшаются с уменьшением a. При этом вещественная ось гиперболы параллельна l₁. При a = 0 гипербола вырождается в пару пересекающихся прямых. Если a < 0 вещественная ось гиперболы параллельна l₂. Полуоси растут с увеличением 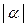. Отношение полуосей для всех гипербол, соответствующих a одного знака, одно и то же. Если нарисовать все сечения гиперболического параболоида на одной и той же плоскости, то получим семейство всех гипербол, имеющих в качестве асимптот пару пересекающихся прямых с уравнением 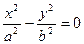. Гиперболический параболоид, как и однополосный гиперболоид, имеет L семейство прямолинейных образующих, уравнения которых следствие:

• конус второго порядка;

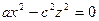Рассмотрим на плоскости Р пару пересекающихся прямых, задаваемую в систему координат 0, l₁, l₃ уравнением: .Поверхность получаемая вращением это линии вокруг оси аппликат, имеет уравнение

(13),

и носит название прямого кругового конуса. Сжатие к плоскости g переводит прямой круговой конус в поверхность с уравнением

(14).

Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение (14), называется конусом второго порядка. Конус состоит из прямых линий, проходящих через начало координат. Сечение конуса плоскостями с уравнениями z = a для различных a представляют собой эллипсы .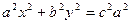

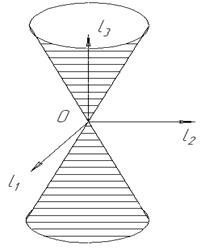
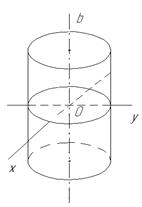
• цилиндры второго порядка;

Рассмотрим уравнение второй степени, не содержащее текущей z.

(15)

Уравнение (15) определяет цилиндр с образующими параллельные оси Oz.

Поскольку уравнение (15) есть уравнение второй степени, определяемое им поверхность называется цилиндром второго порядка.

Уравнение (1) по существу не отличается от уравнения линии второго порядка в декартовых координатах на плоскости. Отсюда заключаем, что сечение рассматриваемого цилиндра плоскостью Oxy есть линия второго порядка.

В зависимости от характера этой линии мы имеем цилиндры второго порядка следующих типов:

1) эллиптический цилиндр; при помощи надлежащего выбора координатной системы его уравнение может быть приведено к виду:

. .

Если a = b, то цилиндр оказывается круговым.

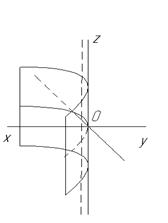
2) гиперболический цилиндр; его уравнение может быть приведено к виду

.

3) Параболический цилиндр; его уравнение может быть приведено к виду

1) 2) 3) .

Кроме того, возможен случай, когда левая часть уравнения (15) есть произведение двух множителей первой степени. Тогда цилиндр «вырождается» в пару плоскостей. Наконец, возможно еще, что уравнение вида (15) совсем не имеет вещественных решений и следовательно, совсем не определяет никакого геометрического образа. Относительно такого уравнения принято говорить, что оно «определяет мнимый цилиндр».