Основной закон динамики вращательного движения

Любая частица вращающегося твердого тела, совершает поступательное движение по окружности под действием внутренних f и внешних F сил согласно уравнению второго закона Ньютона: 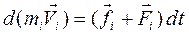. Выведем основное уравнение динамики вращательного движения, которое описывает движение всех частиц тела. Сначала умножим уравнение второго закона Ньютона для одной частицы на радиус-вектор частицы. Этим введём в уравнение динамики моменты сил. Затем запишем столько уравнений, сколько частиц имеет тело, и просуммируем эти уравнения. В результате получим

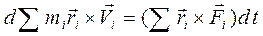. (9.6)

При суммировании исчезли внутренние силы, которые попарно равны и противоположно направлены. Преобразуем уравнение (9.6). Обозначим сумму моментов внешних сил как результирующий момент сил 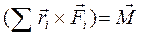. Выразим вектор линейной скорости по формуле связи с угловой скоростью 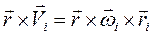, и получим двойное векторное произведение. Раскроем его 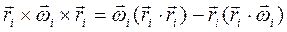. Скалярное произведение в первой скобке равно r², во второй скобке равно нулю (как взаимно перпендикулярных векторов). Подставив преобразования в уравнение (9.6), получим 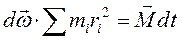. Назовем моментом инерциифизическую величину

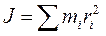. (9.7)

Момент инерции тела равен сумме произведений масс частиц тела на квадраты их расстояний от оси вращения.

Окончательно, основное уравнение динамики вращательного движения запишем в виде

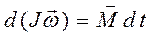. (9.8)

Назовем произведение момента инерции тела на вектор угловой скорости моментом импульса тела 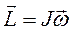, а произведение момента силы на время действия силы импульсом момента силы. Тогда основной закон динамики вращательного движения примет вид: изменение момента импульса тела равно импульсу момента силы.

Так как угловое ускорение тела равно производной от угловой скорости по времени 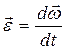, то основной закон динамики вращательного движения при постоянном моменте инерции можно переписать в другом виде

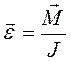. (9.9)

Угловое ускорение тела прямо пропорционально моменту сил, действующих на тело, и обратно пропорционально моменту инерции тела.

Отсюда следует физический смысл момента инерции – это мера инертности тела при вращательном движении. Он является аналогом массы, которая в уравнении второго закона Ньютона является мерой инертности тела в поступательном движении. Но момент инерции зависит не только от массы, но и от ее распределения, по формуле (9.7). Чем дальше от оси вращения находятся части тела, тем больше момент инерции, тем меньше угловое ускорение, тем медленнее раскручивается или тормозит вращающееся тело.