Действия над матрицами

Результатом сложения матриц является матрица, каждый элемент которой представляет собой сумму соответствующих элементов матриц: .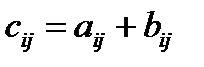

Складываются только матрицы одинаковой размерности.

Результатом умножения матрицы на число является матрица, каждый элемент которой умножен на это число:

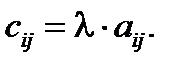
Результатом умножения матриц, будет матрица, каждый элемент которой является результатом перемножения соответствующей строки первой матрицы на соответствующий столбец второй матрицы:

.

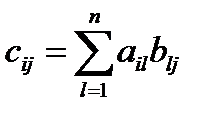Перемножаются только такие две матрицы, у которых число столбцов первой равно числу строк второй матрицы.

Умножение не обладает перестановочным свойством.

Матрицы равны между собой, если равны все соответствующие элементы этих матриц.

Определителемили детерминантом квадратной матрицы называется скаляр, образованный из элементов этой матрицы

.

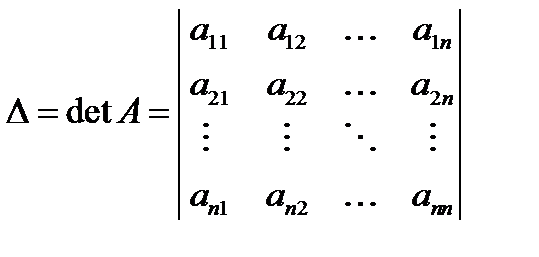Порядком определителя называется число столбцов (строк) квадратной матрицы.

Минором M_ik называется определитель порядка (n–1), полученный из основного определителя, вычеркиванием i-й строки и k-го столбца:

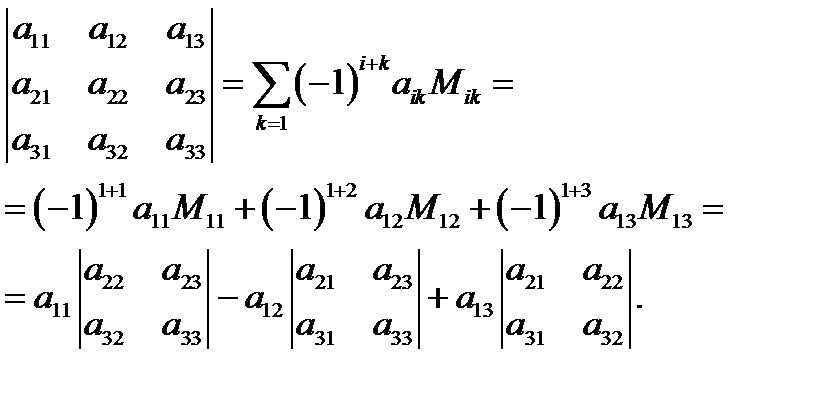
Свойства определителя

1. Определитель n-го порядка сводится к вычислению определителя (n–1) порядка, путем его разложения по какой-либо строке или столбцу (см. выше).

2. Если поменять в определителе местами какие-либо две строки или столбца, то определитель изменит знак.

3. Если какую-либо строку или столбец умножить на число, то полученный определитель будет отличаться от исходного на это же число.

4. Если все элементы какой-либо строки или столбца равны 0, то определитель равен 0.

5. Если в определителе какие-либо две строки или столбца равны между собой, то определитель равен 0.

6. Если к элементам какой-либо строки или столбца прибавить элементы другой строки или столбца, умноженные на любое число, то определитель не изменится.

Определители впервые были введены для решения системы уравнений первой степени. В 1750 г. швейцарский математик Г. Крамер дал общие формулы, выражающие неизвестные через определители, составленные из коэффициентов системы.

Пусть дана система n уравнений с n неизвестными:

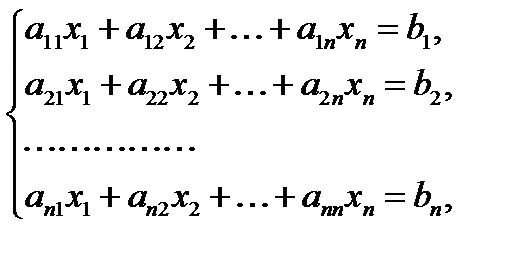
где 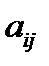– коэффициенты системы, 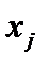– неизвестные, 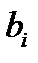– свободные члены.

Систему можно записать в матричной форме:

.

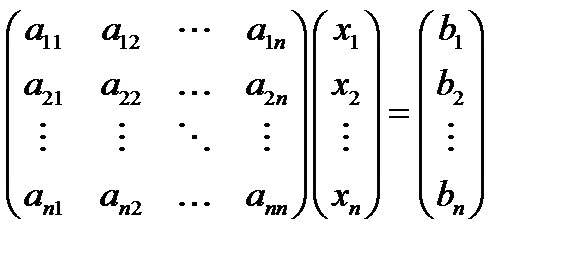Совокупность чисел a₁, a₂, …, a_n или 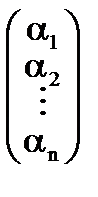называется решением системы, если она обращает все уравнения в тождества.

Система совместна, если она имеет хотя бы одно решение.

Если определитель системы n-го порядка

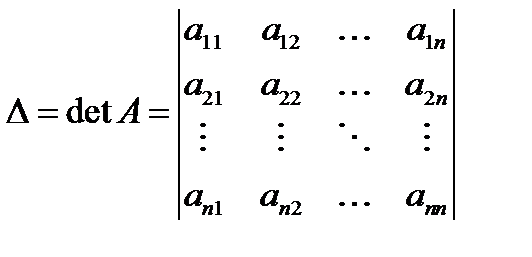
не равен нулю, то система имеет единственное решение:

.

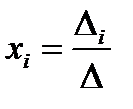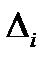Здесь – определитель системы, – дополнительные определители, которые образуются из определителя системы, заменой i-го столбца на столбец свободных членов.

Пример 3. Решить систему уравнений по формулам Крамера

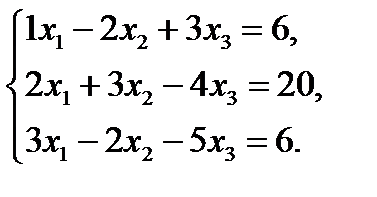
Решение. Найдем определитель системы, составленный из коэффициентов при неизвестных:

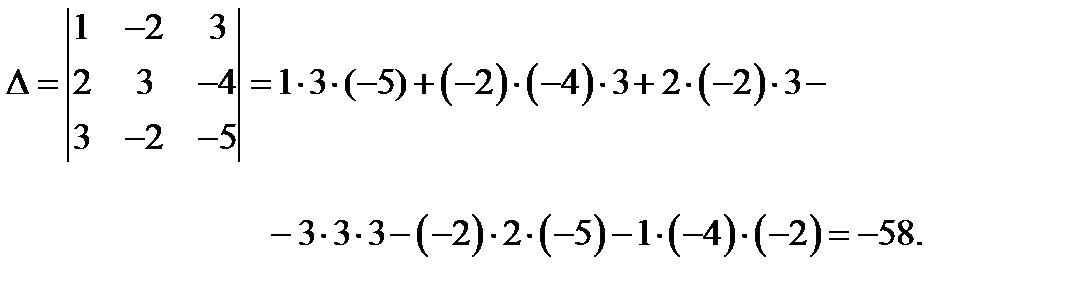
Так как определитель системы не равен нулю ( 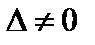), то согласно теореме Крамера, система имеет единственное решение.

Вычислим определители 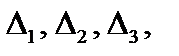полученные из определителя системы заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:

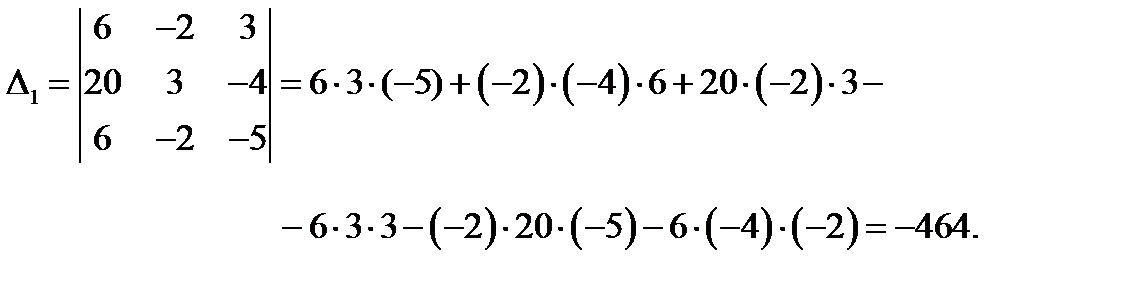
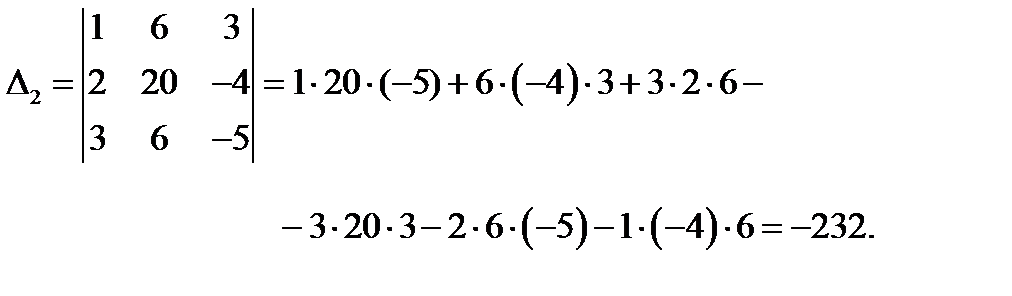
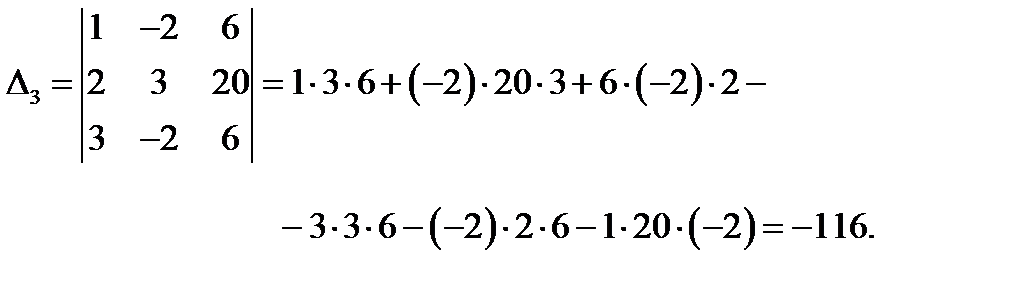
Согласно формулам Крамера найдем решение системы

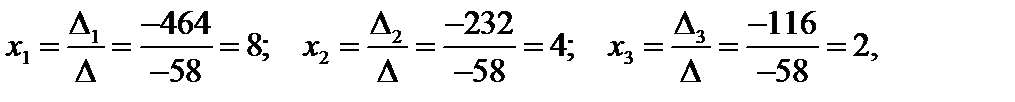
т.е. решение системы: (8; 4; 2). Рекомендуется сделать проверку, подставив найденные значения в уравнения.