Математическая модель импульсного элемента

Применяемые в промышленности импульсные элементы отличаются своим многообразием как по принципу действия и конструкции, так и по характеру эксплуатации. Выходные сигналы реальных импульсных элементов обладают конечной длительностью, и на их форму значительно влияют процессы размыкания и замыкания в цепях. Мощность выходных сигналов в сильной степени зависит от соотношения длительности замыкания элемента и периода следования импульсов. Указанные обстоятельства затрудняют возможность единого подхода при исследовании этих устройств.

Поэтому, чтобы упростить анализ динамических свойств импульсных систем, Я.З. Цыпкиным была выдвинута идея заменить реальное импульсное устройство математической моделью [1]. Широкое распространение получила модель идеального импульсного звена (ИЗ): замыкание и размыкание которого происходят мгновенно и на выходе которого генерируются импульсы типа дельта-функции с нулевой длительностью на конечной площадке.

Реального физического смысла ИЗ не имеет и представляет собой просто полезную математическую абстракцию. Такая модель может использоваться для описания элементов, вырабатывающих импульсы с малой скважностью.

Реальное импульсное устройство (рис. 1.22), выходные сигналы которого имеют произвольную форму и конечную длительность, может представляться как последовательное соединение идеального импульсного звена (ИЗ) и формирующего звена (ФЗ), вырабатывающего импульсы, близкие по форме импульсам реального устройства (рис. 1.23).

Рис. 1.22. Реальное импульсное устройство

Рис. 1.23. Модель импульсного устройства

Для импульсных элементов, генерирующих прямоугольные импульсы, можно построить математическую модель, состоящую из идеального импульсного звена, вырабатывающего последовательности бесконечно тонких импульсов конечной высоты, и фиксаторов, запоминающих значение каждого предыдущего импульса в течение времени, равного ширине импульса .

Рассмотрим импульсное звено.

Пусть несущий или опорный сигнал представляет собой дискретную функцию времени, в общем случае произвольной формы. Ее ординаты имеют конечные значения. Обозначим эту функцию через . Обычно для удобства вычислений нормируется, так что (рис. 1.24), а коэффициент модуляции звена может быть учтен в общем коэффициенте усиления.

0 t

Рис. 1.24. Импульсное звено

Функция характеризует форму выходных импульсов и поэтому иногда называется функцией формы. Форма импульсов может быть самой разнообразной – прямоугольной, треугольной и т.д. В любом случае эта функция для 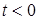и (см. рис. 1.24)

(1.23)

Функция формы позволяет весьма просто записать аналитическое выражение для выходной величины реального импульсного элемента. На самом деле, при произвольном непрерывном входном сигнале выходная величина импульсного элемента для моментов времени

(1.24)

описывается уравнением

(1.25)

Здесь через обозначены импульсы, возникающие на выходе импульсного элемента в моменты времени (рис. 1.25). Из формулы (1.23) следует, что для и . Поэтому выходная величина импульсного элемента для произвольного момента времени t

(1.26)

Из выражения (1.26) следует, что в правой части этого соотношения фигурирует не непрерывный входной сигнал , а только его дискретные значения . Это означает, что импульсный элемент выделяет из входного сигнала только его дискретные значения . Информация о поведении сигнала в промежутках между моментами времени после прохождения этого сигнала через импульсный элемент теряется.

Заменим для удобства анализа реальное импульсное звено последовательным соединением простейшего (идеального) импульсного элемента(ИЭ) и формирователем импульсов (ФИ). Для идеального импульсного элемента функция формы представляет собой единичную дельта-функцию: .

Графически этот элемент изображается в виде ключа (рис. 1.26). Таким образом, импульсный элемент эквивалентен модулятору, в котором в качестве модулирующего сигнала используется входной сигнал , а в качестве несущей – последовательность единичных импульсов .

Будем считать, что все сигналы при t<0 равны нулю.

0 t

Рис. 1.25. Импульсы, возникающие на выходе ИЭ

Рис. 1.26. Графическое обозначение простейшего ИЭ (ключ)

Выходная величина ИЭ представляет последовательность модулированных импульсов

(1.27)

площади амплитуд которых соответствуют последовательности значений входного сигнала .

Дискретное значение определяется выражением для определения площади k-того эквивалентного импульса

. (1.28)

Иными словами, выходной сигнал ИЭ представляет собой последовательность модулированных “по площади” d-функций. Формирующее звено преобразует эту последовательность в последовательность, тождественную по форме импульсов, действующих на выходе реального импульсного устройства.

Достаточно часто в цифровых следящих системах при аналого-цифровом преобразовании используются управляющие импульсы прямоугольной формы со скважностью g=1. При такой форме выходного сигнала применяемое формирующее устройство называется экстраполятором нулевого порядка или фиксатором. Реакция фиксатора на единичный импульс (дельта-функцию) представляет собой функцию веса прямоугольной формы, единичной высоты и длительности, равной периоду дискретности . Используя принцип суперпозиции, этот выходной сигнал можно представить как сумму двух единичных ступенчатых функций (рис. 1.27): 1(t) и –1(t– )

(1.29)

1(t)

–1(t– ) t

Рис. 1.27. Реакция фиксатора на единичный импульс (дельта-функцию)

Так как выражение (1.29) описывает форму выходного импульса, то является функцией формы и одновременно функцией веса . Найдем изображение Лапласа для весовой функции

. (1.30)

Из теории непрерывных АСУ известно, что передаточная функция звена связана с функцией веса прямым преобразованием Лапласа. Таким образом, выражение (1.30) является передаточной функцией экстраполятора нулевого порядка. Из него следует, что формирующее устройство вносит дополнительный отрицательный фазовый сдвиг и временное запаздывание, уменьшая тем самым запас устойчивости АСУ и увеличивая время протекания переходного процесса. Передаточная функция импульсных элементов, вырабатывающих последовательности импульсов малой скважности , может быть найдена по аналогии с выражением (1.30)

(1.31)

так как

Рассмотрим две схемы импульсных АСУ (рис. 1.28 и рис. 1.29).

Рис. 1.28. Схема импульсной системы с ИЭ на входе в систему и в цепи обратной связи

Рис. 1.29. Схема импульсной системы с ИЭ в прямой цепи

В схеме на рис. 1.28 ИЭ стоит на входе в систему и в цепи обратной связи, а в схеме на рис. 1.29 ИЭ стоит в прямой цепи. Однако по своим динамическим свойствам эти схемы идентичны, так как через непрерывные части проходит одинаковый сигнал . Вторая схема проще и более удобна для анализа.

Рассмотрим импульсный элемент.

Пусть сигнал на его выходе имеет вид, показанный на рис. 1.30.

Рис. 1.30. Сигнал на выходе импульсного элемента

Вернемся к схеме преобразования сигнала (рис. 1.31).

Рис. 1.31. Схема преобразования сигнала

Импульсы на выходе ПИЭ можно представить в виде , т.е. в виде дельта-функции с соответствующими значениями их площади. ПИЭ можно представить в виде импульсного модулятора (рис. 1.32) с несущей в виде последовательности импульсов – дельта-функций.

Рис. 1.32. Схема импульсного модулятора

Последовательность единичных импульсов (рис. 1.33) записывают так

(1.32)

Рис. 1.33. Последовательность единичных импульсов

Формирующий элемент характеризуется тем, что его выходной сигнал совпадает по форме с выходным сигналом реального импульсного элемента.