Основные закономерности движения и осаждения пыли
В основу действия пылеулавливающего аппарата положен определенный физический механизм. В пылеулавливающих устройствах находят применение следующие способы отделения взвешенных частиц от взвешивающей среды, т. е. воздуха (газа): осаждение в гравитационном поле, осаждение под действием сил инерции, осаждение в центробежном поле, фильтрование, осаждение в электрическом поле, мокрая очистка и др.
По основному механизму отделения пыли и носит название пылеулавливающий аппарат.
В пылеулавливающем устройстве наряду с основным механизмом улавливания обычно используются и другие закономерности. Благодаря этому общая и фракционная эффективность аппарата достигает более высокого уровня.
Гравитационное осаждение. Пылевые частицы осаждаются из потока запыленного воздуха под действием силы тяжести. Для этого необходимо создать соответствующий режим движения запыленного воздуха в аппарате с учетом размера частиц, их плотности и т. д.
Инерционное осаждение. Инерционное осаждение основано на том, что пылевые частицы и взвешивающая среда ввиду значительной разности плотностей обладают различной инерцией. Пылевые частицы, двигаясь по инерции, отделяются от газовой среды.
Осаждение под действием центробежной силы. Происходит при криволинейном движении пылегазового потока. Под действием возникающих центробежных сил пылевые частицы отбрасываются на периферию аппарата и осаждаются.
Эффект зацепления. Пылевые частицы, взвешенные в воздушной (газовой) среде, задерживаются в узких извилистых каналах и порах при прохождении пылегазового потока через фильтровальные материалы.
Осаждение в электрическом поле. Проходя электрическое поле, пылевые частицы получают заряд. Двигаясь к электродам противоположного знака, они осаждаются на них.
Мокрая очистка. Смачивание поверхности элементов аппаратов водой или другой жидкостью способствует задержанию частиц на данной поверхности.
В практике пылеулавливания находят применение и другие методы: укрупнение частиц в акустическом поле, термофорез, фотофорез, воздействие магнитного поля, биологическая очистка и др.
Гравитационное осаждение
Работа гравитационных пылеулавливающих устройств основана на законах гравитационного осаждения, т. е. осаждения пылевых частиц под действием силы тяжести. В аппаратах, действие которых главным образом зиждется на использовании других сил, также имеют место явления осаждения.
Рассмотрим прямолинейное равномерное движение частицы, подчиняющееся закону Ньютона. Возможные конвективные токи не учитываются.
При движении частица встречает сопротивление среды, которое может быть определено:
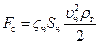 ,
,
где 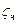 – аэродинамический коэффициент сопротивления частицы;
– аэродинамический коэффициент сопротивления частицы; 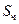 – проекция поперечного сечения частицы на направление ее движения (площадь миделева сечения),
– проекция поперечного сечения частицы на направление ее движения (площадь миделева сечения), 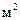 ;
; 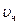 – скорость частицы, м/с;
– скорость частицы, м/с; 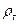 – плотность среды,
– плотность среды, 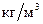 .
.
Коэффициент сопротивления частицы 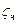 зависит от числа Рейнольдса. Для шаровой частицы:
зависит от числа Рейнольдса. Для шаровой частицы:
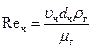 ,
,
где 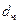 – диаметр частицы, м;
– диаметр частицы, м; 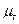 – динамическая вязкость воздуха (газа),
– динамическая вязкость воздуха (газа), 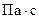 .
.
Соответствующая зависимость приведена на графике, рис. 48. Согласно экспериментальным данным, коэффициенты сопротивления для шаровой пылевой частицы имеют следующие значения (таблица 6):
Таблица 6
Коэффициенты сопротивления для шаровой пылевой частицы
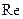 | 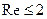 | 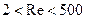 | 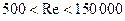 |
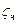 | 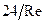 | 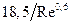 | 0,44 |
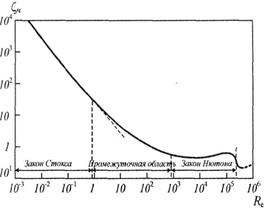
Рис. 48. Зависимость коэффициента лобового сопротивления шаровой частицы 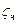 от критерия
от критерия 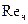
Приняв значение 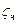 для случая ламинарного движения в области
для случая ламинарного движения в области 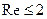 ,
, 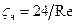 , подставим значение его в формулу Ньютона :
, подставим значение его в формулу Ньютона :
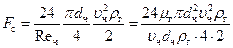 ,
,
получим:
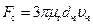 .
.
Эта формула выражает закон Стокса: сила сопротивления, испытываемая твердым шаровым телом при медленном движении в неограниченной вязкой среде, прямо пропорциональна скорости поступательного движения, диаметру тела и вязкости среды.
Закон Стокса применим при ламинарном движении частиц, когда 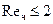 . Область применения закона Стокса практически определяется размерами частиц и требуемой точностью: при
. Область применения закона Стокса практически определяется размерами частиц и требуемой точностью: при 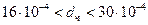 см, неточность составляет 1 %; при
см, неточность составляет 1 %; при 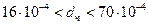 см – 10%. Если допустима большая неточность, можно распространить формулу практически на все размеры пылевых частиц, подвергающихся улавливанию.
см – 10%. Если допустима большая неточность, можно распространить формулу практически на все размеры пылевых частиц, подвергающихся улавливанию.
График, выражающий зависимость 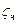 от
от 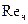 (cм. рис. 48), состоит из трех частей. При
(cм. рис. 48), состоит из трех частей. При 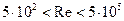 сопротивление характеризуется в области развитой турбулентности законом Ньютона. На этом участке коэффициент сопротивления
сопротивление характеризуется в области развитой турбулентности законом Ньютона. На этом участке коэффициент сопротивления 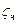 автомоделей относительно числа Рейнольдса
автомоделей относительно числа Рейнольдса 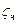 = 44. При
= 44. При 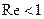 сила сопротивления определяется законом Стокса. Зависимость
сила сопротивления определяется законом Стокса. Зависимость 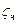 от
от 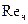 выражается прямым участком в логарифмических координатах.
выражается прямым участком в логарифмических координатах.
Для точных вычислений в закон Стокса вводится поправка Кенингема 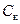 для частиц 0,2–2,0 мкм:
для частиц 0,2–2,0 мкм:
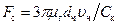 .
.
Ниже приведены значения поправок 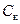 для воздуха при
для воздуха при 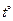 = 20
= 20 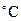 и нормальном атмосферном давлении (таблица 7):
и нормальном атмосферном давлении (таблица 7):
Таблица 7
Значения поправок Кенингема
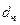 | 0,003 | 0,01 | 0,03 | 0,1 | 0,3 | 1,0 | 3,0 | 10,0 |
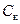 | 90,0 | 24,3 | 7,9 | 2,9 | 1,57 | 1,16 | 1,03 | 1,0 |
Пылевые частицы малых размеров участвуют в броуновском движении– беспорядочном хаотическом перемещении частиц под действием ударов молекул. Чем меньше размер частицы, тем большую роль в ее перемещении играет броуновское движение.
Согласно уравнению Эйнштейна, перемещение частицы в броуновском движении 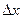 равно:
равно:
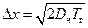 ,
,
где 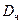 – коэффициент диффузии частицы, характеризующий интенсивность броуновского движения,
– коэффициент диффузии частицы, характеризующий интенсивность броуновского движения, 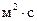 ;
; 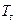 – абсолютная температура воздуха (газа), в котором перемещается частица, К. По имеющимся зависимостям определены скорости осаждения частиц различных размеров и их смещение при броуновском движении за 1 с (табл. 3.1).
– абсолютная температура воздуха (газа), в котором перемещается частица, К. По имеющимся зависимостям определены скорости осаждения частиц различных размеров и их смещение при броуновском движении за 1 с (табл. 3.1).
Таблица 8
Скорости осаждения и броуновского смещения малых частиц
Диаметр частиц 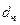 , мкм , мкм | Критерий Рейнольдса | Скорость осаждения, см/с | Броуновское смещение за 1 с, см |
| 13,2 | 1,2 | 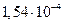 | |
| 0,366 | 0,11 | 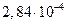 | |
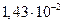 | 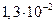 | 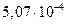 | |
| 0,6 | 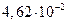 | 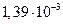 | 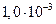 |
| 0,2 | 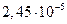 | 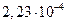 | 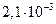 |
| 0,06 | 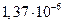 | 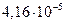 | 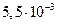 |
| 0,02 | 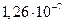 | 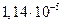 | 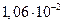 |
Плотность– 1 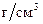 , абсолютная температура – 293 К, вязкость воздуха – , абсолютная температура – 293 К, вязкость воздуха – 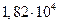 пуаз пуаз |
Как видно из таблица 8, скорость осаждения и величина броуновского смещения соизмеримы для частиц начиная примерно с 0,5 мкм. С уменьшением размера частиц скорость осаждения резко снижается и возрастает броуновское смещение. Для частиц размером 0,05–0,02 мкм оно уже на два–три порядка превышает путь частицы при свободном падении. Поэтому высокодисперсные аэрозольные частицы практически не осаждаются, а благодаря броуновскому движению перемещаются в любом направлении.
Если рассматривается движение нешарообразной частицы, в расчетных формулах значение 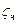 умножается на динамический коэффициент формы
умножается на динамический коэффициент формы 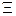 вместо
вместо 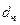 вводят эквивалентный диаметр:
вводят эквивалентный диаметр:
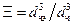 ,
,
где 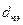 – эквивалентный диаметр частицы, равный диаметру шара, объем которого равен объему данной частицы, м.
– эквивалентный диаметр частицы, равный диаметру шара, объем которого равен объему данной частицы, м.
Таблица 9
Значения 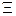 для частиц различной формы
для частиц различной формы
| Шаровая | |
| Округленная с неровной поверхностью | 2,4 |
| Продолговатая | |
| Пластинчатая | |
| Для смешанных тел | 2,9 |
В движении частицы, осаждающейся под действием силы тяжести в неподвижной среде, можно различить три стадии: начальный момент падения; движение с увеличением скорости до того момента, пока силы сопротивления и силы тяжести не уравновесятся; равномерное движение с постоянной скоростью. Первые две стадии имеют чрезвычайно малую продолжительность и обычно специально не рассматриваются.
В области действия закона Стокса скорость осаждения шаровой частицы определяется:
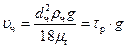 ,
,
где 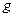 – ускорение свободного падения,
– ускорение свободного падения, 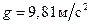 ;
; 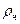 – плотность частицы,
– плотность частицы, 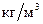 ;
; 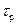 – время релаксации частицы, с.
– время релаксации частицы, с.
Плотностью воздуха (газа) пренебрегаем.
График для определения скорости осаждения частиц пыли различного размера и плотности дан на рис. 49.
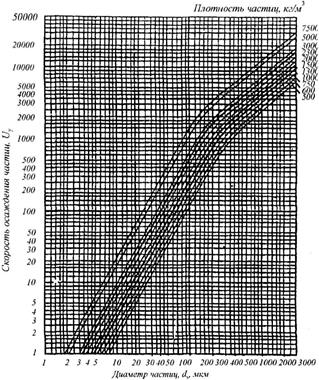
Рис. 49. График для определения скорости осаждения частиц пыли различных размеров и плотности в неподвижном воздухе
Если скорость воздуха равна скорости осаждения и направлена против нее, то скорость осаждения частицы пыли в воздухе равна нулю.
Скорость воздуха в восходящем потоке, при которой частица неподвижна (или совершает колебательные движения), называется скоростью витания.Таким образом, постоянная скорость осаждения частицы пыли в неподвижном воздухе равна скорости ее витания.
Понятие «скорость витания» важно для систем и устройств, в которых происходит перемещение газообразной среды со взвешенными в ней частицами (пневмотранспорт, аспирация, пылеуловители, работающие в основном на принципе гравитации).
Скорость витания пылевых частиц различного размера и плотности может быть определена также с помощью номограммы (рис. 50).
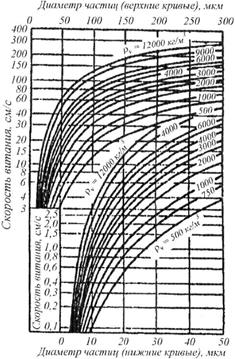
Рис. 50. Номограмма для определения скорости витания частиц пыли
