Значущі, вірні й сумнівні цифри
Значущою цифрою наближеного числа називається будь-яка його цифра починаючи з першої ненульової (рахуючи з ліва на право). Наприклад, у числі 0,00030900 перші чотири нулі не є значущими цифрами. Всі інші цифри (включаючи й наступні три нулі) - значущі.
У цілому округленому числі значущими звичайно вважають всі збережені цифри. Так, в округленому числі 120  цифри 1, 2, 0 — значущі.
цифри 1, 2, 0 — значущі.
Вірною цифрою (вірним знаком) наближеного числа а називається будь-яка його значуща цифра, для якої абсолютна похибка 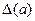 не перевершує половини розряду цієї цифри. Інші значущі цифри числа а називаються сумнівними.
не перевершує половини розряду цієї цифри. Інші значущі цифри числа а називаються сумнівними.
Таким чином, якщо 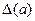
 , то цифри числа а, починаючи з першої значущої й кінчаючи стоячою в n-м розряді після коми,— вірні, а розташовані далі—сумнівні. Наприклад, число 647,326 при
, то цифри числа а, починаючи з першої значущої й кінчаючи стоячою в n-м розряді після коми,— вірні, а розташовані далі—сумнівні. Наприклад, число 647,326 при 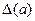 =0,03
=0,03 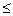 0,5
0,5  має чотири вірні цифри 6, 4, 7, 3 і дві сумнівні 2, 6.
має чотири вірні цифри 6, 4, 7, 3 і дві сумнівні 2, 6.
У математичних таблицях значень функцій приводяться тільки вірні цифри. Абсолютна похибка табличних значень, наприклад, у тризначних таблицях не перевершує 0,5  , у семизначних — 0,5
, у семизначних — 0,5  .
.
Точність наближеного числа залежить не від кількості значущих цифр, а від кількості вірних цифр.
Остаточний наближений результат звичайно округляють до його вірних цифр, залишаючи одну сумнівну. При розрахунках з наближеними числами в проміжних результатах зберігають одну, дві, а іноді й три сумнівні цифри.
Приклад 3. Задані числа при зазначених абсолютних похибках округлити до вірних цифр. Визначити абсолютну похибку результату:
1) а1 =2,6219,  = 0,024; 2) а2 = 47,35,
= 0,024; 2) а2 = 47,35,  = 1,3;
= 1,3;
3) а3 = 6,9971,  = 0,0009; 4) а4=0,648,
= 0,0009; 4) а4=0,648,  = 0,04.
= 0,04.
Розв’язання. 1) Оскільки 0,024 < 0,05, то число а1 варто округлити до 0,1. Одержимо число а1  2,6 з двома вірними цифрами. Визначимо абсолютну похибку результату
2,6 з двома вірними цифрами. Визначимо абсолютну похибку результату
 = 0,024 + | 2,6219 - 2,6 | = 0,0459
= 0,024 + | 2,6219 - 2,6 | = 0,0459  0,05.
0,05.
2) Оскільки 1,3 < 0,5  , то число а2 варто округлити до десятків. Одержимо число а2
, то число а2 варто округлити до десятків. Одержимо число а2  5•10 з однією вірною цифрою. Абсолютна похибка результату
5•10 з однією вірною цифрою. Абсолютна похибка результату
 = 1,3 + 2,65 = 3,95
= 1,3 + 2,65 = 3,95  4.
4.
3) Оскільки 0,0009 < 0,005, то округлення числа робимо до 0,01. Одержимо число а3  7,00 з трьома вірними цифрами. Абсолютна похибка результату
7,00 з трьома вірними цифрами. Абсолютна похибка результату
 = 0,0009 + | 7,00 - 6,9971 | = 0,0038
= 0,0009 + | 7,00 - 6,9971 | = 0,0038  0,004.
0,004.
У числі 7,00 записані нулі свідчать про три його вірні знаки й цей запис відрізняється від 7 або 7,0.
4) Оскільки 0,04 < 0,05, то число а4 округляємо до 0,1. Одержимо число а4  0,6 з однією вірною цифрою. Абсолютна похибка результату
0,6 з однією вірною цифрою. Абсолютна похибка результату
 = 0,04 + 0,048 = 0,088 > 0,05,
= 0,04 + 0,048 = 0,088 > 0,05,
т. е. цифра 6 уже сумнівна. Тому при округленні рекомендується залишати одну-дві сумнівні цифри, тобто
а4  0,65,
0,65,  = 0,042
= 0,042  0,05.
0,05.
Підмітимо, що термін «вірні цифри» не слід розуміти буквально. Так, у числі 7,00, що заміняє число 6,9971, всі знаки вірні |6,9971 - 7,00| < 0,005, але жодна із цифр чисел 6,9971 й 7,00 не збігається. Однак вірні знаки наближеного числа часто збігаються з відповідними цифрами точного числа.
Абсолютна похибка визначає число десяткових знаків наближеного числа.
Відносна похибка наближеного числа безпосередньо залежить від числа його вірних знаків. Є спеціальні таблиці, що визначають відносні похибки залежно від числа вірних знаків. Так, наприклад, якщо наближене число а має три вірних знаки, те його відносна похибка 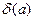 перебуває в межах від 0,05 до 0,5 % (залежить від першої значущої цифри числа а). При збільшенні числа вірних знаків на 1 відносна похибка зменшується в 10 разів.
перебуває в межах від 0,05 до 0,5 % (залежить від першої значущої цифри числа а). При збільшенні числа вірних знаків на 1 відносна похибка зменшується в 10 разів.
Зауваження. На практиці звичайно вважають, що число а є наближенням числа а0 з п вірними десятковими знаками, якщо  .
.
При такому визначенні в числі а = 647,35 при 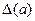 = 0,095 < 0,1 будуть вірними цифри 6, 4, 7, 3. Відповідно до колишнього визначення, оскільки
= 0,095 < 0,1 будуть вірними цифри 6, 4, 7, 3. Відповідно до колишнього визначення, оскільки 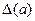 < 0,5, у цьому числі будуть вірними лише цифри 6, 4, 7. У подальших розділах в основному використається це визначення вірних цифр наближеного числа.
< 0,5, у цьому числі будуть вірними лише цифри 6, 4, 7. У подальших розділах в основному використається це визначення вірних цифр наближеного числа.
