Необратимость и вероятность

Все процессы, связанные с тепловым движением молекул отличаются от механических движений, тем, что они бывают необратимыми. Между тем сами по себе движения каждой молекулы подчиняются законам механики. Возникает вопрос, каким образом, совокупность частиц, каждый из которых подчиняется законам механики и движения которых обратимо, способна только к необратимым изменениям состояния. Причиной этого является большее количество частиц и полная хаотичность их движений.

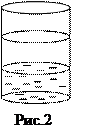
Рассмотрим пример. Пусть сосуд объёмом V заполнен воздухом (рис.2). Мысленно разобьём объём сосуда на 3 части, каждая из которых имеет объём V^’. Введём в одну из них, например в нижнюю, постороннюю молекулу, например, молекулу эфира. За счёт хаотичных движений эта молекула покинет нижний объём и в результате своего дальнейшего движения будет попадать на все из 3 частей сосуда, в том числе и в ту, которую только что покинула. Переход из незаштрихованной области в заштрихованную область является обратимым, поскольку без внешнего воздействия она может вернуться в заштрихованную область. Если каждую секунду контролировать её местонахождение, то в одном из трех наблюдений мы обнаружим её в объёме V’.

Введём понятие вероятности: вероятностью события называется предел, к которому стремится отношение числа опытов, приводящих к его осуществлению, к общему числу опытов при бесконечном увеличении последнего.

Значит, вероятность обнаружить молекулу в заштрихованном объёме V^’ равна 1/3. Вероятность эта велика, чтобы процесс считать обратимым. Если мы введём две молекулы, то вероятность их одновременного нахождения в V’ ровно (1/3)², поскольку эти события независимые, а вероятность независимых событий равно произведению вероятностей этих событий. Эта вероятность уже значительно меньше, так, что процесс перехода двух молекул из V в V’ уже с меньшим правом считается обратимым. Если введём 3, 4, 5 молекул эфира, то вероятность их обнаружить будет соответственна (1/3)³, (1/3)⁴, (1/3)⁵. С ростом числа частиц эфира, первоначально введённых в V’, вероятность вновь обнаружить их там становится всё меньше, следовательно, всё менее обратимым становится естественный процесс перемешивание частиц эфира и воздуха.

Обобщая только что приведённый пример, мы можем сказать, что если из объёма V выделить объём 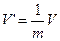, то вероятность W того, что N частиц окажутся в этой выделенной части равна 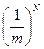. Если N велико, то W очень мала. Представим себе тогда, что в пустом лишённом газа сосуде объёмом V выделен объем 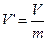, отделённый от остального объёма перегородкой. Введём в V’ N молекул и уберём перегородку. Ясно, после этого газ, его частицы заполнят объём V. Если T=const, то это изотермическое расширение газа от объёма V’ до V. Такое расширение представляет собой изменение состояния газа и мы уже должны говорить о большей или малой вероятности состояния.

В нашем случае речь идёт о переходе из состояния с V’ в состояние с объемом V. Вероятность первого равна 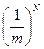, поскольку 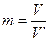, а

.

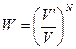Что касается состояния с объемом V, то вероятность этого состояния равна единице.

Вероятность W состояния, при которой газ помещается в части объёма V^’ вместо того, чтобы занять его целиком, при больших значениях N очень мала. В этом и заключается причины необратимости естественного протекания процессов. Газ сам собой распространяется по всему объёму, но никогда не концентрируется в части этого объёма. Но это не говорит, что этот процесс невозможен. Законы механики, которым подчиняется молекулы, разрешают оба направления процесса, но из-за большего количества частиц вероятность одного из них настолько мала, что проистечение невозможно наблюдать.

Во всех случаях само собой происходит переход к равновесному состоянию, вероятность которого велика. Но обратный переход к неравновесному состоянию практически не происходит, потому что вероятность такого состояния мала. Значит необратимость процессов в молекулярных системах, состоящих из частиц, каждая из которых подчиняется законам механики, т.е. движется обратимо, объясняется исключительно тем, что очень великое число этих частиц. Будь их немного, система не знала никаких необратимых процессов.

Цикл Карно

Одним из процессов, часто происходящих в природе при переходе какой-нибудь системы к равновесию является превращение механической энергии в тепловую. Выделение тепла за счёт механической энергии – это процесс превращение макроскопической энергии в энергию микроскопических тепловых движений. Обратный этому процесс – это превращение тепловой энергии в механическую или получение механической энергии за счёт тепла

Иногда результатом произведённой механической работы может явиться возникновение равного количества тепла. Это значит, что энергия макроскопического движения целиком переходит в энергию микроскопических движений молекул вещества, т. е. механическая работа может полностью превратиться в теплоту. Возникает вопрос – тепловая энергия может ли полностью перейти в механическую работу. Для этого рассмотрим цикл Карно, в процессе которого тепловая энергия преобразуется в механическую работу.

Для того чтобы теплота могла быть использована для получения работы, необходимо каким – то образом отнять у тела часть его тепловой энергии. Это можно сделать, приводя в соприкосновение другое тело с более низкой температурой. Благодаря теплопроводности тепло будет передаваться от одного тела к другому. Это необратимый процесс, он не сопровождается совершением работы, так как в этом процессе нет никакого перемещения тел. Таким образом, простой обмен теплом двух соприкасающихся тел различной температуры не может привести к совершению работы. Необходимо третье тело, которое бы принимало тепло от более нагретого тела, перемещаясь при этом, передавало бы его менее нагретому и при этом оно совершило бы механическую работу. Это промежуточное тело будем называть рабочим телом. Более нагретое тело назовём нагревателем, более холодное тело холодильником. Процесс получения тепла от нагревателя и передачи к холодильнику должен произойти при одинаковых температурах. В противном случае необратимый процесс теплопроводности будет приводить к бесполезной потере теплоты. Всё сказанное относится к реально существующим установкам для превращения тепла в механическую работу (паровые машины, турбины, двигатели внутреннего сгорания), которые действуют циклически, т. е. процесс передачи энергии от нагретого тела к холодному телу периодически повторяется. Рабочее тело, совершив определённые процессы, при которых через его посредство от нагревателя к холодильнику было передано некоторое количество теплоты, а им совершена некоторая работа, возвращается в исходное состояние, чтобы снова начать весь процесс. Другими словами рабочее тело претерпевает круговой процесс – т. е. совершает цикл. Работа, совершаемая во время кругового процесса равна поглощаемому количеству теплоты, т.е. Q=A

Рассмотрим круговой процесс, при котором тепло, отнятое от какого-нибудь тела, можно превратить в работу, так чтобы эта работа была максимальной. Чтобы осуществит этот процесс нужно иметь три тела: нагреватель – рабочее тело – холодильник. Предположим, что нагреватель и холодильник имеют большую теплоёмкость, так что за счёт отданного или полученного тепла их температуры не меняются (рис.3).

Начнём круговой процесс над рабочим телом с того, что оно сжатое до некоторого давления, находится в контакте с нагревателем и имеет такую же температуру, что и нагреватель. Процесс теплопроводности при этом не происходит, так как нет разности температур. Таким образом, не происходит передача тепла без совершения работы. Представим рабочему телу возможность расшириться, оставаясь в контакте с нагревателем. AB – изотермическое расширение. При этом будет совершена работа. Она будет совершена за счёт тепла отнятого у нагревателя. Полученное тепло нужно передать холодильнику. Это нельзя осуществить при непосредственном соприкосновении рабочего тела с холодильником, потому что тепло будет переходить к холодильнику без совершения полезной работы. Рабочее тело нужно охладить до температуры холодильника. Для охлаждения рабочее тело должно быть теплоизолированным от нагревателя и испытывать адиабатическое расширение. При этом рабочее тело охлаждается и совершает работу. В точке C рабочее тело приводят в соприкосновение с холодильником. При этом завершается первая половина цикла, во время которого тело совершает полезную работу за счёт тепла, полученного от нагревателя.

Сейчас рабочее тело надо вернуть к исходному состоянию. Это делается в два этапа: CD – изотермическое сжатие, во время которого рабочее тело находится в контакте с холодильником, DA – адиабатическое сжатие до температуры нагревателя, при этом оно нагревается за счёт внешней работы, совершаемой над ним. Рабочее тело приводят в соприкосновение с нагревателем. При сжатии работа совершается внешними силами. На всех стадиях кругового процесса не допускается соприкосновения тел с различной температурой, т. е. весь процесс идёт обратимо. Это цикл Карно. В результате первого процесса Карно некоторое количество тепла оказывается переданным посредством рабочего тела от нагревателя к холодильнику. В ходе этого процесса рабочее тело совершает некоторую работу. Во второй половине процесса над рабочим телом совершают работу внешние силы. Получается ли при этом полезная механическая работа.

Для этого рабочее тело представим как идеальный газ. Пусть рабочее тело представляет 1 моль идеального газа и пусть исходное состояние характеризуется точкой A(P_o,V_o). Температура газа 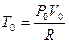равна температуре нагревателя, T₁- температура холодильника. Значит T₀>T₁. При изотермическом расширении на участке АВ совершается работа

A₁=RT₀ln 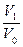=Q₀ ,

где Q₀- количество теплоты отнятое газом у нагревателя. Bо втором этапе газ изолируется от нагревателя и дальнейшее его расширение происходит адиабатно, вследствие чего газ охлаждается. Это адиабатическое расширение продолжается до тех пор, пока температура газа не станет равной температуре холодильника. Значит, объём V₂, до которого должен расшириться газ определяется из уравнения адиабаты

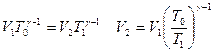. (1.33)

Работа, совершаемая во втором процессе на участке ВС равна

.

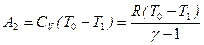Таким образом, вся положительная работа, совершаемая газом при его расширении равна

.

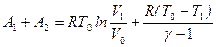На третьем этапе (участок СД) газ изотермически сжимается внешними силами при температуре холодильника Т₁ от объема V₂ до объема V₃. При этом совершается работа

,

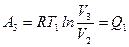которая выделяется в виде тепла и передаётся холодильнику.

В последнем этапе ДА происходит адиабатное сжатие до исходного объема V₀ давления Р₀, при которых температура станет равной Т₀. Для этого необходимо, чтобы объем V₃, до которого изотермически сжимается газ, определился следующим образом

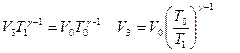(1.34)

Работа сжатия на этом этапе равна

.

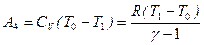Газ теперь опять в первоначальном состоянии, цикл Карно завершен, и процесс можно снова начать. Общая работа, совершенная газом, равна

.

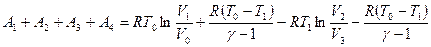Из формул (1.33) и (1.34) следует

.

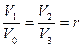Следовательно, общая работа

,

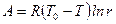и так как 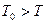, то A>0. Значит, работа, совершаемая газом при расширении, больше работы внешних сил, затраченной на его сжатие. За счёт теплоты, полученной рабочим телом от нагревателя, совершена, таким образом, некоторая полезная работа. Это работе не равно количеству теплоты Q₀, которое рабочее тело получило от нагревателя. Из отданного нагревателем количества тепла

.

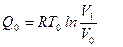часть равная

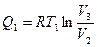
было передано холодильнику. В полезную работу удалось преобразовать лишь часть полученной теплоты, равную

.

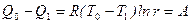Этим процесс преобразования теплоты в работу отличается от обратного процесса преобразования работы в тепло (механическая работа может превратиться в тепло полностью).

Из полученных выше соотношений для Q₀, Q₁, Q₀-Q₁ следует важное выражение

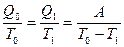. (1.35)