Метод ньютона, его реализации и модификации
Пусть 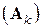 – некоторая последовательность невырожденных вещественных
– некоторая последовательность невырожденных вещественных 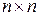 -матриц. Тогда, очевидно, последовательность задач
-матриц. Тогда, очевидно, последовательность задач
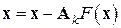 ,
, 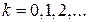
имеет те же решения, что и исходное уравнение (7.lа), и для приближенного нахождения этих решений можно формально записать итерационный процесс
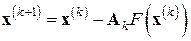 ,
, 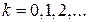 (7.5)
(7.5)
имеющий вид метода простых итераций (7.3) при 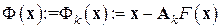 . В случае
. В случае 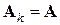 это, как показано в конце предыдущего параграфа, – действительно МПИ с линейной сходимостью последовательности
это, как показано в конце предыдущего параграфа, – действительно МПИ с линейной сходимостью последовательности 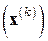 . Если же
. Если же 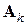 различны при разных
различны при разных 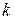 , то формула (7.5) определяет большое семейство итерационных методов с матричными параметрами
, то формула (7.5) определяет большое семейство итерационных методов с матричными параметрами 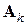 . Рассмотрим некоторые из методов этого семейства.
. Рассмотрим некоторые из методов этого семейства.
Положим 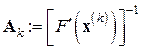 , где
, где
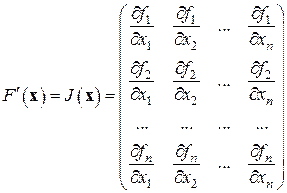
– матрица Якоби вектор-функции 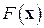 . Подставив это
. Подставив это 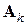 в (7.5), получаем явную формулу метода Ньютона
в (7.5), получаем явную формулу метода Ньютона
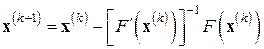 , (7.6)
, (7.6)
обобщающего на многомерный случай скалярный метод Ньютона. Эту формулу, требующую обращения матриц на каждой итерации, можно переписать в неявном виде:
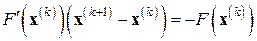 . (7.7)
. (7.7)
Применение (7.7) предполагает при каждом 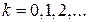 решение линейной алгебраической системы
решение линейной алгебраической системы
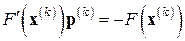
относительно векторной поправки 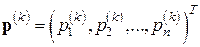 , а затем прибавление этой поправки к текущему приближению для получения следующего:
, а затем прибавление этой поправки к текущему приближению для получения следующего:
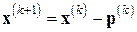 .
.
К решению таких линейных систем можно привлекать самые разные методы как прямые, так и итерационные (см. гл. 2, 3) в зависимости от размерности  решаемой задачи и специфики матриц Якоби
решаемой задачи и специфики матриц Якоби 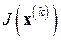 (например, можно учитывать их симметрию, разреженность и т.п.).
(например, можно учитывать их симметрию, разреженность и т.п.).
Сравнивая (7.7) с формальным разложением 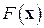 в ряд Тейлора
в ряд Тейлора
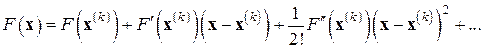 ,
,
видим, что последовательность 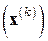 в методе Ньютона получается в результате подмены при каждом
в методе Ньютона получается в результате подмены при каждом 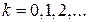 нелинейного уравнения
нелинейного уравнения 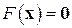 или, что то же (при достаточной гладкости
или, что то же (при достаточной гладкости 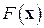 ), уравнения
), уравнения
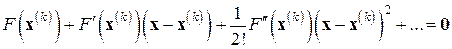
линейным уравнением
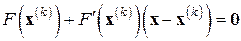 ,
,
т.е. пошаговой линеаризацией. Как следствие этого факта, можно рассчитывать, что при достаточной гладкости 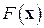 и достаточно хорошем начальном приближении
и достаточно хорошем начальном приближении 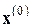 сходимость порождаемой методом Ньютона последовательности
сходимость порождаемой методом Ньютона последовательности 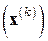 к решению
к решению 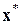 будет квадратичной.
будет квадратичной.
Фактором, осложняющим применение метода Ньютона к решению  -мерных систем, является необходимость решения
-мерных систем, является необходимость решения  -мерных линейных задач на каждой итерации (обращения матриц в (7.6) или решения СЛАУ в (7.7), вычислительные затраты на которые растут с ростом
-мерных линейных задач на каждой итерации (обращения матриц в (7.6) или решения СЛАУ в (7.7), вычислительные затраты на которые растут с ростом  , вообще говоря, непропорционально быстро. Уменьшение таких затрат – одно из направлений модификации метода Ньютона.
, вообще говоря, непропорционально быстро. Уменьшение таких затрат – одно из направлений модификации метода Ньютона.
Если матрицу Якоби 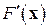 вычислить и обратить лишь один раз – в начальной точке
вычислить и обратить лишь один раз – в начальной точке 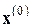 , то от метода Ньютона (7.6) придем к модифицированному методу Ньютона
, то от метода Ньютона (7.6) придем к модифицированному методу Ньютона
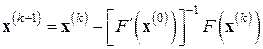 . (7.8)
. (7.8)
Этот метод требует значительно меньших вычислительных затрат на один итерационный шаг, но итераций при этом может потребоваться значительно больше для достижения заданной точности по сравнению с основным методом Ньютона (7.6), поскольку, являясь частным случаем МПИ (с 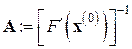 ), он имеет лишь скорость сходимости геометрической прогрессии.
), он имеет лишь скорость сходимости геометрической прогрессии.
Компромиссный вариант – это вычисление и обращение матриц Якоби не на каждом итерационном шаге, а через несколько шагов (иногда такие методы называют рекурсивными).
Например, простое чередование основного (7.6) и модифицированного (7.8) методов Ньютона приводит к итерационной формуле
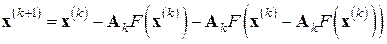 , (7.9)
, (7.9)
где 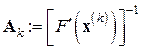 ,
, 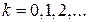 . За
. За 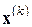 здесь принимается результат последовательного применения одного шага основного, а затем одного шага модифицированного метода, т.е. двухступенчатого процесса
здесь принимается результат последовательного применения одного шага основного, а затем одного шага модифицированного метода, т.е. двухступенчатого процесса
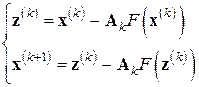 (7.10)
(7.10)
Доказано, что такой процесс при определенных условиях порождает кубически сходящуюся последовательность 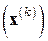 .
.
Задачу обращения матриц Якоби на каждом 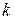 -м шаге метода Ньютона (7.6) можно попытаться решать не точно, а приближенно. Для этого можно применить, например, итерационный процесс Шульца (см. § 6.6), ограничиваясь минимумом – всего одним шагом процесса второго порядка, в котором за начальную матрицу принимается матрица, полученная в результате предыдущего
-м шаге метода Ньютона (7.6) можно попытаться решать не точно, а приближенно. Для этого можно применить, например, итерационный процесс Шульца (см. § 6.6), ограничиваясь минимумом – всего одним шагом процесса второго порядка, в котором за начальную матрицу принимается матрица, полученная в результате предыдущего 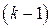 -го шага. Таким образом, приходим к методу Ньютона с последовательной аппроксимацией обратных матриц:
-го шага. Таким образом, приходим к методу Ньютона с последовательной аппроксимацией обратных матриц:
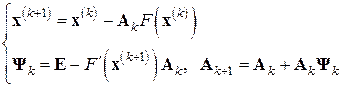 , (7.11)
, (7.11)
где 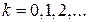 , а
, а 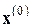 и
и 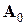 – начальные вектор и матрица
– начальные вектор и матрица 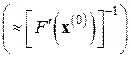 соответственно. Этот метод (будем называть его более коротко ААМН – аппроксимационный аналог метода Ньютона) имеет простую схему вычислений – поочередное выполнение векторных в первой строке и матричных во второй строке его записи (7.11) операций. Скорость его сходимости почти так же высока, как и у метода Ньютона. Последовательность
соответственно. Этот метод (будем называть его более коротко ААМН – аппроксимационный аналог метода Ньютона) имеет простую схему вычислений – поочередное выполнение векторных в первой строке и матричных во второй строке его записи (7.11) операций. Скорость его сходимости почти так же высока, как и у метода Ньютона. Последовательность 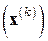 может квадратично сходиться к решению
может квадратично сходиться к решению 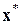 уравнения
уравнения 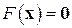 (при этом матричная последовательность
(при этом матричная последовательность 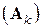 также квадратично сходится к
также квадратично сходится к 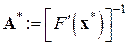 , т.е. в нормально развивающемся итерационном процессе (7.11) должна наблюдаться достаточно быстрая сходимость
, т.е. в нормально развивающемся итерационном процессе (7.11) должна наблюдаться достаточно быстрая сходимость 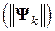 к нулю).
к нулю).
Применение той же последовательной аппроксимации обратных матриц к простейшему рекурсивному методу Ньютона (7.9) или, что то же, к двухступенчатому процессу (7.10) определяет его аппроксимационный аналог
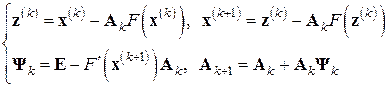 , (7.12)
, (7.12)
который, как и (7.9), также можно отнести к методам третьего порядка. Доказательство кубической сходимости этого метода требует уже более жестких ограничений на свойства 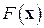 и близость
и близость 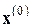 к
к 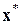 ,
, 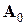 к
к 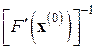 , чем в предыдущем методе. Заметим, что к улучшению сходимости здесь может привести повышение порядка аппроксимации обратных матриц, например, за счет добавления еще одного слагаемого в формуле для подсчета:
, чем в предыдущем методе. Заметим, что к улучшению сходимости здесь может привести повышение порядка аппроксимации обратных матриц, например, за счет добавления еще одного слагаемого в формуле для подсчета:
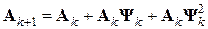 .
.
На базе метода Ньютона (7.6) можно построить близкий к нему по поведению итерационный процесс, не требующий вычисления производных. Сделаем это, заменив частные производные в матрице Якоби 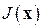 разностными отношениями, т.е. подставив в формулу (7.5) вместо
разностными отношениями, т.е. подставив в формулу (7.5) вместо 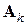 матрицу
матрицу 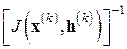 , где
, где
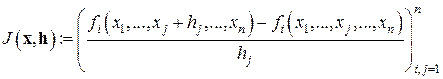
При удачном задании последовательности малых векторов 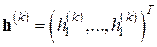 (постоянной или сходящейся к нулю) полученный таким путем разностный (или иначе, дискретный) метод Ньютона
(постоянной или сходящейся к нулю) полученный таким путем разностный (или иначе, дискретный) метод Ньютона
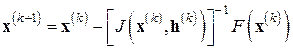 (7.13)
(7.13)
имеет сверхлинейную, вплоть до квадратичной, скорость сходимости. При задании векторного параметра 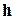 – шага дискретизации – следует учитывать точность машинных вычислений (macheps), точность вычисления значений функций
– шага дискретизации – следует учитывать точность машинных вычислений (macheps), точность вычисления значений функций 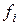 , средние значения получаемых приближений.
, средние значения получаемых приближений.
Можно связать задание последовательности 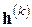 с какой-либо сходящейся к нулю векторной последовательностью, например, с последовательностью невязок
с какой-либо сходящейся к нулю векторной последовательностью, например, с последовательностью невязок 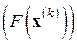 или поправок
или поправок 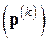 . Так, полагая
. Так, полагая 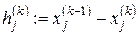 , где
, где 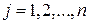 , а
, а 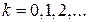 , приходим к простейшему методу секущих:
, приходим к простейшему методу секущих:
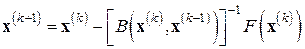 (7.14)
(7.14)
где
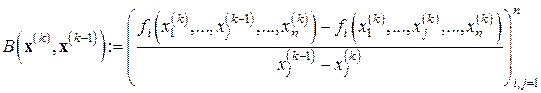 ,
, 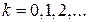
Этот метод является двухшаговым и требует задания двух начальных точек 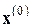 и
и 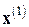 . При
. При 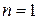 сходимость метода (7.14) имеет порядок
сходимость метода (7.14) имеет порядок 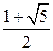 . Можно рассчитывать на такую же скорость и в многомерном случае.
. Можно рассчитывать на такую же скорость и в многомерном случае.
К методу секущих так же, как и к методу Ньютона, можно применить пошаговую аппроксимацию обратных матриц на основе метода Шульца. Расчетные формулы этой модификации легко выписать, заменив в совокупности формул ААМН (7.11) матрицу 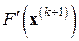 на матрицу
на матрицу 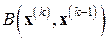 из (7.14).
из (7.14).
Замечание 7.1. Для останова процесса вычислений в быстросходящихся методах таких, как метод Ньютона, методы секущих и т.п., часто вполне успешно применяют простой критерий:
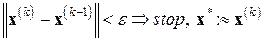 . (7.15)
. (7.15)
Это можно объяснить двумя причинами. Во-первых, оценки погрешности здесь довольно «дороги». Имеется в виду как их получение (особенно для различных модификаций базовых методов), так и их реальное применение. Во-вторых, в силу своей быстрой сходимости, к моменту достижения требуемой малости нормы поправки эти методы набирают такую инерцию, что зачастую «проскакивают» установленный порог точности, т.е. выход по критерию (7.15) дает значение 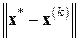 значительно (иногда на несколько порядков) меньшее, чем
значительно (иногда на несколько порядков) меньшее, чем 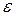 . Отслеживать факт сходимости в процессе итераций для того, чтобы реагировать на возможную расходимость в случаях, когда заранее не обеспечены условия сходимости применяемого метода, можно с помощью текущих проверок на уменьшение от шага к шагу поправок и невязок, т.е. выполнение неравенств
. Отслеживать факт сходимости в процессе итераций для того, чтобы реагировать на возможную расходимость в случаях, когда заранее не обеспечены условия сходимости применяемого метода, можно с помощью текущих проверок на уменьшение от шага к шагу поправок и невязок, т.е. выполнение неравенств
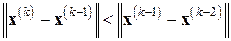 и
и 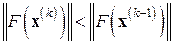 . (7.16)
. (7.16)
МЕТОД БРАУНА
В отличие от пошаговой линеаризации векторной функции 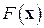 , приведшей к методу Ньютона (7.6), Брауном (1966 г.), предложено проводить на каждом итерационном шаге поочередную линеаризацию компонент вектор-функции
, приведшей к методу Ньютона (7.6), Брауном (1966 г.), предложено проводить на каждом итерационном шаге поочередную линеаризацию компонент вектор-функции 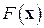 , т.е. линеаризовать в системе (7.1) сначала функцию
, т.е. линеаризовать в системе (7.1) сначала функцию 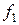 затем
затем 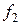 и т.д., и последовательно решать получаемые таким образом уравнения. Чтобы не затенять эту идею громоздкими выкладками и лишними индексами, рассмотрим вывод расчетных формул метода Брауна в двумерном случае.
и т.д., и последовательно решать получаемые таким образом уравнения. Чтобы не затенять эту идею громоздкими выкладками и лишними индексами, рассмотрим вывод расчетных формул метода Брауна в двумерном случае.
Пусть требуется найти решение системы
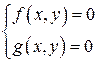 , (7.17)
, (7.17)
и пусть уже получены приближения 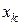 ,
, 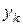 .
.
Подменим первое уравнение системы (7.17) линейным, полученным по формуле Тейлора для функции двух переменных:
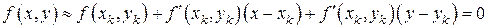 .
.
Отсюда выражаем 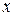 (обозначим этот результат через
(обозначим этот результат через 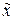 ):
):
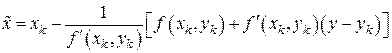 . (7.18)
. (7.18)
При 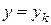 находим значение
находим значение 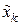 переменной
переменной 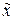 :
:
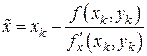 ,
,
которое будем считать лишь промежуточным приближением (т.е. не 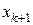 ), поскольку оно не учитывает второго уравнения системы (7.17).
), поскольку оно не учитывает второго уравнения системы (7.17).
Подставив в 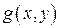 вместо
вместо 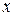 переменную
переменную 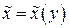 , придем к некоторой функции
, придем к некоторой функции 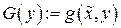 только одной переменной
только одной переменной 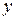 . Это позволяет линеаризовать второе уравнение системы (7.17) с помощью формулы Тейлора для функции одной переменной:
. Это позволяет линеаризовать второе уравнение системы (7.17) с помощью формулы Тейлора для функции одной переменной:
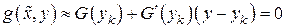 . (7.19)
. (7.19)
При нахождении производной 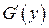 нужно учесть, что
нужно учесть, что 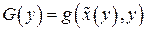 есть сложная функция одной переменной
есть сложная функция одной переменной 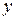 , т.е. применить формулу полной производной
, т.е. применить формулу полной производной
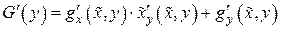 .
.
Дифференцируя по 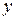 равенство (7.18), получаем выражение
равенство (7.18), получаем выражение
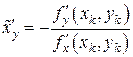 ,
,
подстановка которого в предыдущее равенство при 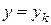 ,
, 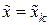 дает
дает
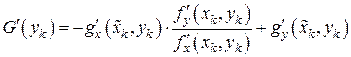 .
.
При известных значениях 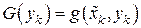 и
и 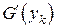 теперь можно разрешить линейное уравнение (7.19) относительно
теперь можно разрешить линейное уравнение (7.19) относительно 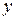 (назовем полученное значение
(назовем полученное значение 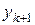 ):
):
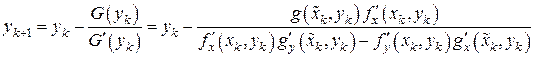 .
.
Заменяя в (7.18) переменную 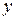 найденным значением
найденным значением 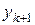 приходим к значению
приходим к значению 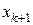 :
:
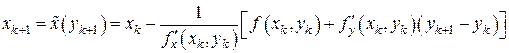 .
.
Таким образом, реализация метода Брауна решения двумерных нелинейных систем вида (7.17) сводится к следующему.
При выбранных начальных значениях 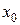 ,
, 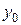 каждое последующее приближение по методу Брауна находится при
каждое последующее приближение по методу Брауна находится при 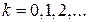 с помощью совокупности формул
с помощью совокупности формул
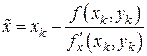
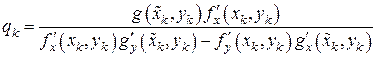
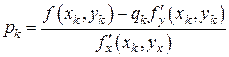
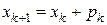 ,
, 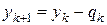
счет по которым должен выполнятся в той очередности, в которой они записаны.
Вычисления в методе Брауна естественно заканчивать, когда выполнится неравенство 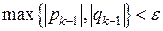 с результатом
с результатом 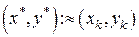 ). В ходе вычислений следует контролировать немалость знаменателей расчетных формул. Заметим, что функции
). В ходе вычислений следует контролировать немалость знаменателей расчетных формул. Заметим, что функции 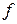 и
и 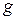 в этом методе неравноправны, и перемена их ролями может изменить ситуацию со сходимостью.
в этом методе неравноправны, и перемена их ролями может изменить ситуацию со сходимостью.
Указывая на наличие квадратичной сходимости метода Брауна, отмечают, что рассчитывать на его большую по сравнению с методом Ньютона эффективность в смысле вычислительных затрат можно лишь в случае, когда фигурирующие в нем частные производные заменяются разностными отношениями.
МЕТОД СЕКУЩИХ БРОЙДЕНА
Чтобы приблизиться к пониманию идей, лежащих в основе предлагаемого вниманию метода рассмотрим одномерный случай
В процессе построения методов Ньютона и секущих решения нелинейного скалярного уравнения.
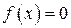 (7.20)
(7.20)
функция 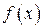 в окрестности текущей точки
в окрестности текущей точки 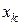 подменяется линейной функцией (аффинной моделью)
подменяется линейной функцией (аффинной моделью)
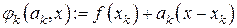 (7.21)
(7.21)
Приравнивание к нулю последней, т.е. решение линейного уравнения
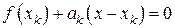
порождает итерационную формулу
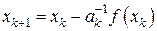 (7.22)
(7.22)
для вычисления приближений к корню уравнения (7.20).
Если потребовать, чтобы заменяющая функцию 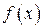 вблизи точки
вблизи точки 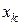 аффинная модель
аффинная модель 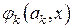 имела в этой точке одинаковую с ней производную, то, дифференцируя (7.21), получаем значение коэффициента
имела в этой точке одинаковую с ней производную, то, дифференцируя (7.21), получаем значение коэффициента
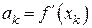
подстановка которого в (7.22) приводит к известному методу Ньютона. Если же исходить из того, что наряду с равенством 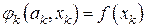 должно иметь место совпадение функций
должно иметь место совпадение функций 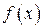 и
и 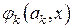 в предшествующей
в предшествующей 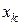 точке
точке 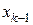 т.е. из равенства
т.е. из равенства
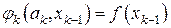 ,
,
или, в соответствии с (7.21),
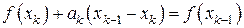 , (7.23)
, (7.23)
то получаем коэффициент
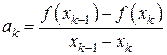 ,
,
превращающий (7.22) в известную формулу секущих.
Равенство (7.23), переписанное в виде
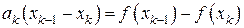 ,
,
называют соотношением секущих в 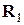 . Оно легко обобщается на
. Оно легко обобщается на  -мерный случай и лежит в основе вывода метода Бройдена. Опишем этот вывод.
-мерный случай и лежит в основе вывода метода Бройдена. Опишем этот вывод.
В  -мерном векторном пространстве
-мерном векторном пространстве 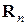 соотношение секущих представляется равенством
соотношение секущих представляется равенством
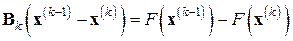 , (7.24)
, (7.24)
где 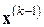 ,
, 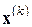 – известные
– известные  -мерные векторы,
-мерные векторы, 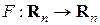 – данное нелинейное отображение, а
– данное нелинейное отображение, а 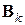 – некоторая матрица линейного преобразования в
– некоторая матрица линейного преобразования в 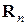 . С обозначениями
. С обозначениями
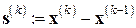 ,
,  , (7.25)
, (7.25)
соотношение секущих в 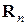 обретает более короткую запись:
обретает более короткую запись:
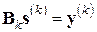 . (7.24а)
. (7.24а)
Аналогично одномерному случаю, а именно, по аналогии с формулой (7.22), будем искать приближения к решению 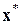 векторного уравнения (7.1а) по формуле
векторного уравнения (7.1а) по формуле
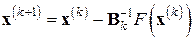 . (7.26)
. (7.26)
Желая, чтобы эта формула обобщала метод секущих, обратимую 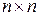 -матрицу
-матрицу 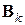 в ней нужно подобрать так, чтобы она удовлетворяла соотношению секущих (7.24). Но это соотношение не определяет однозначно матрицу
в ней нужно подобрать так, чтобы она удовлетворяла соотношению секущих (7.24). Но это соотношение не определяет однозначно матрицу 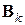 : глядя на равенство (7.24а), легко понять, что при
: глядя на равенство (7.24а), легко понять, что при 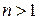 существует множество матриц
существует множество матриц 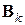 , преобразующих заданный
, преобразующих заданный  -мерный вектор
-мерный вектор 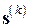 в другой заданный вектор
в другой заданный вектор 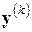 .
.
При формировании матрицы 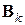 будем рассуждать следующим образом.
будем рассуждать следующим образом.
Переходя от имеющейся в точке 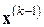 аффинной модели функции
аффинной модели функции 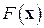
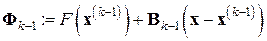 (7.27)
(7.27)
к такой же модели в точке 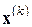
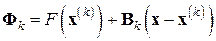 , (7.28)
, (7.28)
мы не имеем о матрице линейного преобразования 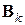 никаких сведений, кроме соотношения секущих (7.24). Поэтому исходим из того, что при этом переходе изменения в модели должны быть минимальными. Эти изменения характеризуют разность
никаких сведений, кроме соотношения секущих (7.24). Поэтому исходим из того, что при этом переходе изменения в модели должны быть минимальными. Эти изменения характеризуют разность 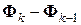 . Вычтем из равенства (7.28) определяющее
. Вычтем из равенства (7.28) определяющее 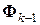 равенство (7.27) и преобразуем результат, привлекая соотношение секущих (7.24). Имеем:
равенство (7.27) и преобразуем результат, привлекая соотношение секущих (7.24). Имеем:
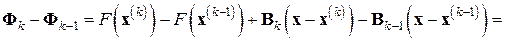
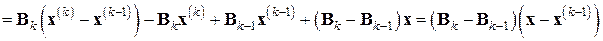 .
.
Представим вектор 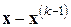 в виде линейной комбинации фиксированного вектора
в виде линейной комбинации фиксированного вектора 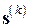 , определенного в (7.25), и некоторого вектора
, определенного в (7.25), и некоторого вектора 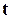 , ему ортогонального:
, ему ортогонального:
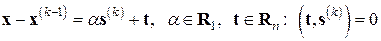 .
.
Подстановкой этого представления вектора 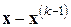 в разность
в разность 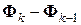 получаем другой ее вид
получаем другой ее вид
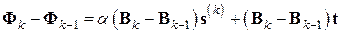 . (7.29)
. (7.29)
Анализируя выражение (7.29), замечаем, что первое слагаемое в нем не может быть изменено, поскольку
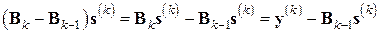
– фиксированный вектор при фиксированном 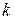 . Поэтому минимальному изменению аффинной модели
. Поэтому минимальному изменению аффинной модели 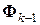 будет отвечать случай, когда второе слагаемое в (7.29) будет нуль-вектором при всяких векторах
будет отвечать случай, когда второе слагаемое в (7.29) будет нуль-вектором при всяких векторах 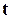 , ортогональных векторам
, ортогональных векторам 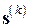 , т.е.
, т.е. 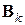 следует находить из условия
следует находить из условия
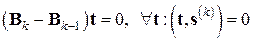 . (7.30)
. (7.30)
Непосредственной проверкой убеждаемся, что условие (7.30) будет выполнено, если матричную поправку 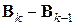 взять в виде одноранговой
взять в виде одноранговой  -матрицы
-матрицы
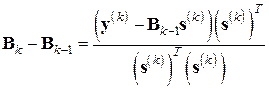 .
.
Таким образом, приходим к так называемой формуле пересчета С. Бройдена (1965 г.)
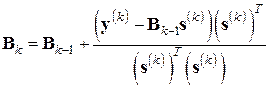 , (7.31)
, (7.31)
которая позволяет простыми вычислениями перейти от старой матрицы 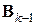 к новой
к новой 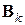 такой, чтобы выполнялось соотношение секущих (7.24а) в новой точке и при этом изменения в аффинной модели (7.27) были минимальны (строго доказано, что такое построение отвечает минимальности поправки
такой, чтобы выполнялось соотношение секущих (7.24а) в новой точке и при этом изменения в аффинной модели (7.27) были минимальны (строго доказано, что такое построение отвечает минимальности поправки 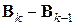 по норме Фробениуса на множестве матриц
по норме Фробениуса на множестве матриц 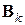 удовлетворяющих соотношению секущих (7.24а)).
удовлетворяющих соотношению секущих (7.24а)).
Совокупность формул (7.26), (7.31) вместе с обозначениями (7.25) называют методом секущих Бройдена или просто методом Бройдена решения систем нелинейных числовых уравнений.
Хотя в методах секущих обычным является задание двух начальных векторов 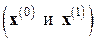 , для метода Бройдена характерно другое начало итерационного процесса. Здесь нужно задать один начальный вектор
, для метода Бройдена характерно другое начало итерационного процесса. Здесь нужно задать один начальный вектор 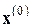 , начальную матрицу
, начальную матрицу 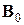 и далее в цикле по
и далее в цикле по 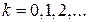 последовательно выполнять следующие операции:
последовательно выполнять следующие операции:
1. решить линейную систему
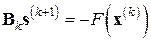 (7.32)
(7.32)
относительно вектора 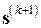 (см. (7.26));
(см. (7.26));
2. найти векторы 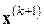 и
и 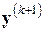 (см. (7.25)):
(см. (7.25)):
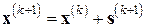 ,
, 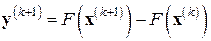 ; (7.33)
; (7.33)
3. сделать проверку на останов (например, с помощью проверки на малость величин 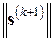 и/или
и/или 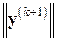 ) и, если нужная точность не достигнута, вычислить новую матрицу
) и, если нужная точность не достигнута, вычислить новую матрицу 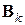 по формуле (см. (7.31))
по формуле (см. (7.31))
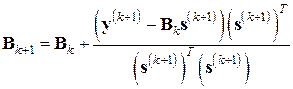 . (7.34)
. (7.34)
В качестве матрицы 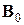 , требуемой равенством (7.32) для запуска итерационного процесса Бройдена, чаще всего берут матрицу Якоби
, требуемой равенством (7.32) для запуска итерационного процесса Бройдена, чаще всего берут матрицу Якоби 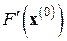 или какую-нибудь ее аппроксимацию. При этом, как отмечается, получаемые далее пересчетом (7.34) матрицы
или какую-нибудь ее аппроксимацию. При этом, как отмечается, получаемые далее пересчетом (7.34) матрицы 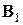 ,
, 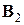 , ... не всегда можно считать близкими к соответствующим матрицам Якоби
, ... не всегда можно считать близкими к соответствующим матрицам Якоби 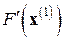 ,
, 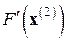 , ... (что может иногда сыграть полезную роль при вырождении матриц
, ... (что может иногда сыграть полезную роль при вырождении матриц 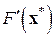 ). Но, в то же время, показывается, что при определенных требованиях к матрицам Якоби
). Но, в то же время, показывается, что при определенных требованиях к матрицам Якоби 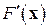 матрицы
матрицы 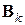 обладают «свойством ограниченного ухудшения», означающим, что если и происходит увеличение
обладают «свойством ограниченного ухудшения», означающим, что если и происходит увеличение 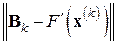 с увеличением номера итерации
с увеличением номера итерации 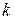 , то достаточно медленно. С помощью этого свойства доказываются утверждения о линейной сходимости
, то достаточно медленно. С помощью этого свойства доказываются утверждения о линейной сходимости 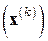 к
к 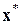 при достаточной близости
при достаточной близости 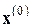 к
к 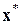 и
и 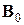 к
к 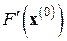 , а в тех предположениях, при которых можно доказать квадратичную сходимость метода Ньютона (7.6), – о сверхлинейной сходимости последовательности приближений по методу Бройдена.
, а в тех предположениях, при которых можно доказать квадратичную сходимость метода Ньютона (7.6), – о сверхлинейной сходимости последовательности приближений по методу Бройдена.
Как и в случаях применения других методов решения нелинейных систем, проверка выполнимости каких-то условий сходимости итерационного процесса Бройдена весьма затруднительна и обычно заменяется проверками на выполнимость неравенств типа (7.16).
Формуле пересчета (7.34) в итерационном процессе Бройдена можно придать чуть более простой вид.
Так как, в силу (7.32) и (7.33),
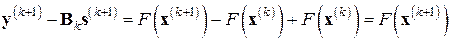 ,
,
а
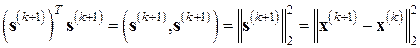 ,
,
то из формулы (7.34) получаем формально эквивалентную ей формулу пересчета
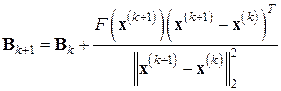 , (7.35)
, (7.35)
которую можно использовать вместо (7.34) в совокупности с формулой (7.26) или с (7.32), (7.33) (без вычисления вектора 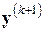 ). Такое преобразование итерационного процесса Бройдена несколько сокращает объем вычислений (на одно матрично-векторное умножение на каждой итерации). Не следует, правда, забывать, что при замене формулы (7.34) формулой (7.35) может измениться ситуация с вычислительной устойчивостью метода; к счастью, это случается здесь крайне редко, а именно, в тех случаях, когда для получения решения с нужной точностью требуется много итераций по методу Бройдена, т.е. когда и применять его не стоит.
). Такое преобразование итерационного процесса Бройдена несколько сокращает объем вычислений (на одно матрично-векторное умножение на каждой итерации). Не следует, правда, забывать, что при замене формулы (7.34) формулой (7.35) может измениться ситуация с вычислительной устойчивостью метода; к счастью, это случается здесь крайне редко, а именно, в тех случаях, когда для получения решения с нужной точностью требуется много итераций по методу Бройдена, т.е. когда и применять его не стоит.
