Обобщенное уравнение Бернулли

Дифференциальное уравнение первого закона термодинамики в виде

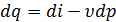
применительно к движущемуся в потоке объему газа, учитывая, что теплота dq может подводиться к нему как извне, так и за счет трения, может быть записано так: .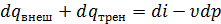

Для вывода уравнения Бернулли запишем уравнение сохранения энергии и уравнение первого закона термодинамики в дифференциальном виде

.

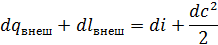
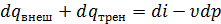Вычтем второе уравнение из первого, учитывая, что 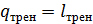, тогда

.

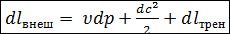Это уравнение называется обобщенным уравнением Бернулли в дифференциальной форме.

Проинтегрировав это уравнение от сечения 1-1 до сечения 2-2 (рис. 4.2), получим обобщенное уравнение Бернулли в интегральной форме.

.

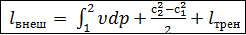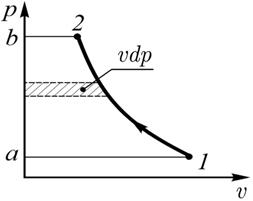Рис. 4.3

Интеграл 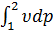эквивалентен пло­щади между осью ординат и кривой процесса (площадь 12bа, рис. 4.3). Этот интеграл в теории газотурбинных двигателей называется работой сжатия газа в потоке. Хотя, по существу, это работа, затрачиваемая на повышение давления, т.е. на сжатие (уменьшение объема) газа и на работу по его продвижения («проталкивания») далее по потоку.

Отметим, что 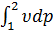также называют политропной работы газового потока.

Таким образом, согласно обобщенному уравнению Бернулли внешняя работа, подведенная к газу в потоке, расходуется на работу сжатия газа, на изменение (увеличение) его кинетической энергии и на работу по преодолению трения.

Обобщенное уравнение Бернулли мо­жно интерпретировать как баланс меха­нических форм энергии в газовом пото­ке.

Наличие трения, естественно, скажется на параметрах потока. Например, при заданном уров­не понижения давления ( 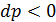) наличие трения ( 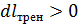), как видно из дифференциального уравнения Бернулли, понизит при­рост скорости потока. А в случае торможения потока при заданном уровне понижения скорости при наличии трения давление возрастет в меньшей степени, чем без трения, или вообще не возрастет.

Действительно, если течение газа происходит в канале (во входном устройстве, газопроводе и т.п.), в котором нет подвода (или отвода) внешней работы ( 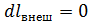), то согласно дифференциальному уравнению Бернулли

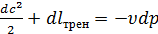или .

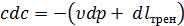Если же течение происходит при этом без трения, то

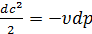или ,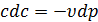

т.е. в таком случае разгон газового потока (dc > 0) возможен только за счет понижения его давления (dp < 0). Наоборот, понижение скорости при отсутствии трения будет приводить к росту давления.

Величину политропной работы газового потока 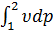в любом политропном процессе вычислим, определив значение 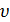из уравнения политропы и подставив его под знак интеграла. Действительно, т.к. 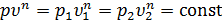, то 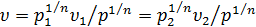и тогда

.
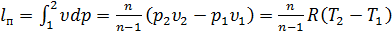