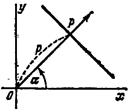
Связь между декартовыми и полярными координатами
Пару полярных координат 
и 
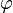можно перевести в Декартовы координаты 
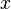и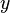 
путём применения тригонометрических функций синуса и косинуса:
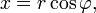
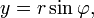
20. Чтобы перейти от общего уравнения прямой (3.8)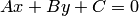 
к уравнению с угловым коэффициентом (3.18), нужно разрешить общее уравнение относительно неизвестной 
:
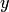21.
22.
;
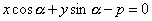уравнение этого вида называется нормальным.
Общее уравнение прямой имеет вид: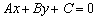 
23. Условия параллельности двух прямых:
а: <k1 =< k2
б)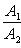 
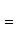
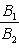
Условия перпендикулярности двух прямых: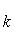 
(
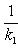
24. Если задано уравнение прямой Ax + By + C = 0 то расстояние
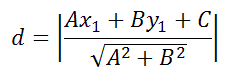
Пучком прямых на плоскости называется множество всех прямых данной плоскости, имеющих одну общую точку, которая называется центром пучка.Уравнение пучка: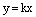 
, где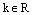 
, есть уравнение пучка
25. Эллипсом называется множество точек на плоскости, сумма расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная.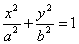 
26.Гипербола — это множество точек плоскости, модуль разности расстояний которых от двух точек, называемых фокусами, есть величина постоянная.
Основные понятия
1. Гипербола состоит из двух отдельных кривых, которые называют ветвями.
2. Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.
3. Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.
4. Середина большой оси называется центром гиперболы.
5. Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы. Обычно обозначается a.
6. Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием. Обычно обозначается c.
7. Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы.
8. Прямая, перпендикулярная действительной оси и проходящая через её центр, называется мнимой или сопряженной осью гиперболы.
9. Отрезок между фокусом гиперболы и гиперболой, перпендикулярный к её действительной оси, называется фокальным параметром.
10. Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром. Обычно обозначается b.
o Каноническое уравнение гиперболы в декартовых координатах:x2 / a2 - y2 / b2 = 1
o Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:xox / a2 - yoy / b2 = 1или y = yo + (b2xo)(x - xo) / (a2yo)Уравнение нормали к гиперболе имеет вид:y = yo - (a2yo)(x - xo) / (b2xo)