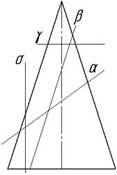
Тема: Параллельность на чертеже Плоскости Σ(ABCD) параллельна прямая l

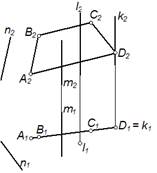
Прямой l, изображенной на чертеже, параллельна прямая b

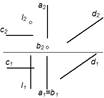
Две параллельные прямые показаны на рисунке 3

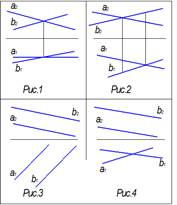
Если две плоскости параллельны, то две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.

Если две плоскости перпендикулярны одной и той же прямой, то эти плоскости параллельны

Две прямые параллельны в пространстве, если их одноименные проекции

параллельны

Прямая, параллельная плоскости, показана на рисунке 4

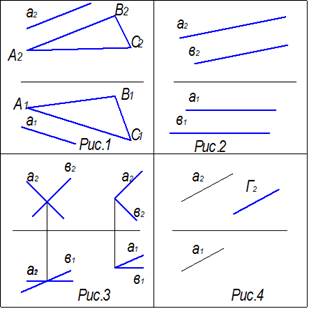
Тема: Пересечение прямой с плоскостью и пересечение двух плоскостей
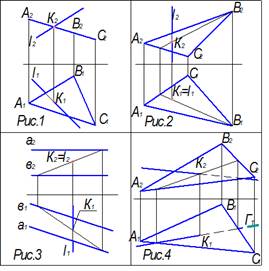
Линией пересечения двух плоскостей, изображенных на рисунке, является фронтально-проецирующая прямая

Прямая общего положения и проецирующая плоскость пересекаются на рисунке …

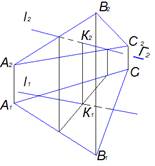
Плоскость общего положения и прямая общего положения пересекаются на чертеже

Плоскость общего положения и проецирующая прямая пересекаются на чертеже

Пересечение проецирующей плоскости и прямой общего положения проиллюстрировано на рисунке 1

Тема: Пересечение поверхностей
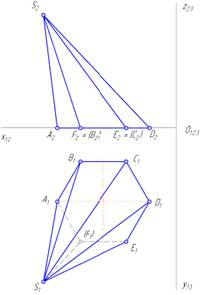
Минимальный радиус вспомогательной секущей сферы определяется отрезком О ₂ F ₂

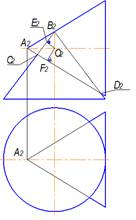
Две соосные поверхности вращения пересекаются по окружностям

Линии пересечения конуса и цилиндра, описанных вокруг одной сферы, на фронтальной плоскости проекций изображаются в виде прямолинейных отрезков

Для построения линии пересечения поверхностей, изображенных на рисунке, применяют способ концентрических сфер

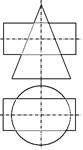
При построении линии пересечения поверхностей способом секущих плоскостей вспомогательные плоскости выбирают так, чтобы при пересечении их с заданными поверхностями получались окружности или прямые

Окружность, по которой пересекаются сфера и конус, на профильную плоскость проекций проецируется в прямую

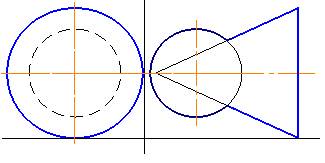
Заданные на чертеже поверхности цилиндров пересекаются по двум эллипсам

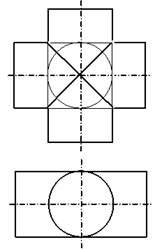
Тема: Принадлежность точки и линии плоскости и поверхности
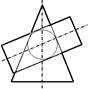
Плоскости принадлежит точка F

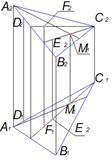
Плоскости Σ(m∩n) принадлежат точки B иD

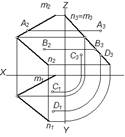
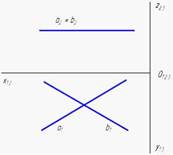
Из точек, показанных на чертеже, выше всех расположена точка А, ближе всех к наблюдателю расположена точкаD

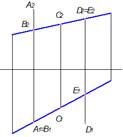
Поверхности сферы принадлежит точка L

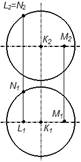
Поверхности конуса принадлежит точка L

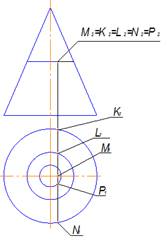
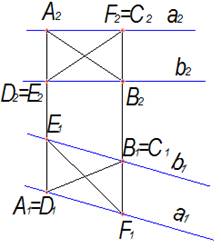
Плоскости (a || b) принадлежит прямая АВ и ЕF

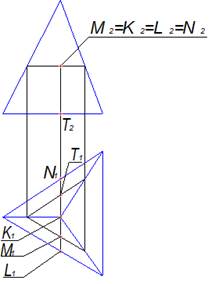
Поверхности пирамиды принадлежит точка M

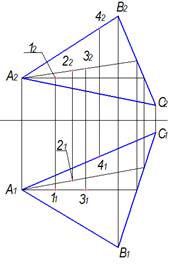
Из представленных на чертеже точек плоскости принадлежит точка 3

Тема: Прямоугольный чертеж точки на две и три плоскости проекций
Линии, соединяющие проекции точек на двухкартинном комплексном чертеже, называются линиями связи

Равноудалены от профильной плоскости проекций точки А и В

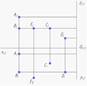
Равноудалены от фронтальной плоскости проекций точки В и D

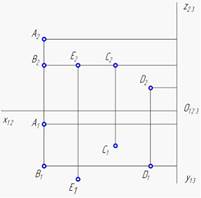
Дальше других точек от горизонтальной плоскости проекций находится точка C

Ближе других точек к профильной плоскости проекций находится точка D

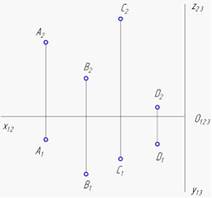
На данном чертеже профильная проекция построена для точки B

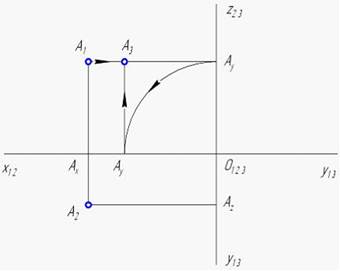
Даны фронтальная и горизонтальная проекции точки А, расположенной в третьей четверти пространства. Верно процесс построения профильной проекции точки А показан на чертеже (Задание точки двумя проекциями равносильно заданию точки тремя координатами. Так как профильная и фронтальная проекции точки должны быть расположены на одном перпендикуляре к оси Oz, то через А₂ проводят прямую А₂А_z ^ Oz. Расстояние от оси Oz равно значению ординаты А_у точки А, тоесть А₃А_z = А_у. Если А_у < 0, как в данном случае (так как точка находится в III четверти пространства), то расстояние А_у откладывается влево от оси Oz.)

Тема: Чертеж прямой линии, чертеж плоскости
Плоскость общего положения показана на рисунке …

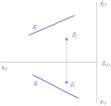
Горизонтально-проецирующая плоскость показана на рисунке …

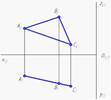
Фронтально-проецирующая плоскость показана на рисунке

Изображенная на чертеже плоскость a (DABC) расположена ^ П₁

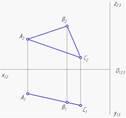
Изображенная на чертеже плоскость a (а Ç b) расположена // П₂

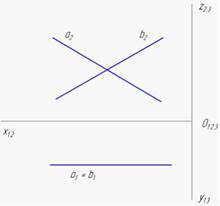
Плоскость общего положения показана на рисунке

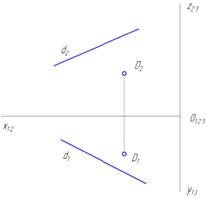
Профильная прямая уровня показана на рисунке

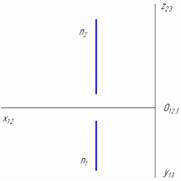
Горизонтальная плоскость уровня показана на рисунке

Тема: Метод проекций, виды проецирования
Свойство – «Изображение проецирующей прямой вырождается в точку» – является инвариантным (неизменным) для любого вида проецирования.

Однозначно судить о положении точки в пространстве можно по двум или более проекции(-ям) точки.

При центральном проецировании проекции параллельных прямых в общем случае пересекаются

Для центрального проецирования не является инвариантным (неизменным) следующее свойство сохраняется пропорциональность параллельных отрезков

Если угол между проецирующими лучами и плоскостью проекций отличен от 0° и 90°, то такое проецирование называется косоугольным

Свойство – «Если линии пересекаются, то их изображения пересекаются в проекции точки пересечения оригиналов» – является инвариантным (неизменным) для любого вида проецирования

Свойство – «Проекция отрезка не может быть больше своей натуральной величины» – является инвариантным (неизменным) только для ортогонального проецирования.

При центральном проецировании каждая точка пространства имеет только одну центральную(-ые) проекцию(-ии).

Свойство геометрических фигур, заключающееся в том, что если точка принадлежит линии, то и проекция точки принадлежит соответствующей проекции линии, выполняется для любого способа проецирования.

При параллельном проецировании проекции параллельных прямых в общем случае параллельны

При ортогональном проецировании, если проецируемая фигура занимает произвольное положение по отношению к плоскости проекции, ее проекция не сохраняет угловые и линейные величины.

Если направление проецирования перпендикулярно плоскости проекций, то такое проецирование называется ортогональным (прямоугольным)

Тема: Чертеж многогранника. Чертеж поверхности вращения
На рисунке показан двухкартинный комплексный чертеж прямой трехгранной призмы

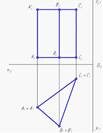
На чертеже задана пятигранная пирамида SACDEF. Элемент пирамиды ASC называется боковой гранью пирамиды.

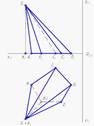
На рисунке показан двухкартинный комплексный чертеж наклонной трехгранной призмы

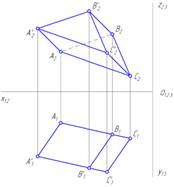
На горизонтальной проекции усеченной пирамиды ABCA’B’C’ невидимой гранью является грань ABC

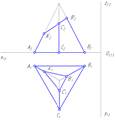
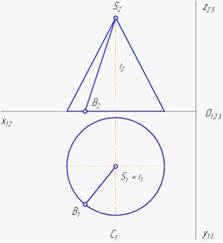
На рисунке показан двухкартинный комплексный чертеж прямого кругового конуса. Отрезок SВ является образующей конуса.

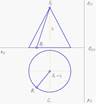
Видимость ребер и граней шестигранной наклонной пирамиды правильно определена на чертеже

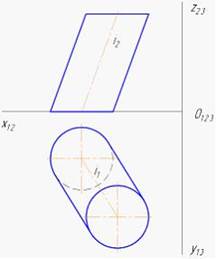
На рисунке показан двухкартинный комплексный чертеж поверхности вращения. Образующей данной поверхности является линия

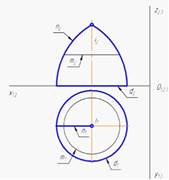
Не относится к поверхностям вращения фигура, показанная на чертеже

Геометрическим элементом, вращением отрезка вокруг которого получена поверхность прямого кругового конуса, является прямая i

Тема: Классификация плоских и пространственных кривых
Винтовая коническая с постоянным шагом линия проецируется на плоскость, перпендикулярную оси, в спираль Архимеда.

Пространственной кривой линией является винтовая

Плоская кривая линия изображена на рисунке

Плоской кривой линией является спираль Архимеда

На рисунке изображены проекции конической винтовой линии

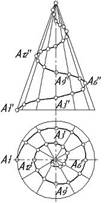Винтовая коническая с постоянным шагом линия проецируется на плоскость, перпендикулярную оси, в спираль Архимеда.

Плоская кривая второго порядка, ортогональная проекция которой может быть окружностью или эллипсом, называется окружностью

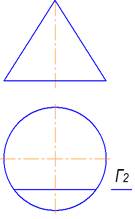
Плоскость Г пересекает конус по двум прямым

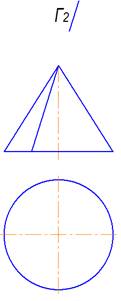
Плоскость Г пересекает конус по гиперболе

Винтовая коническая с постоянным шагом линия проецируется на плоскость, перпендикулярную оси, в спираль Архимеда.

Тема: Поверхности
При перемещении прямолинейной образующей l по криволинейной направляющей m (причем одна из точек прямой l остается всегда неподвижной) образуется коническая поверхность.

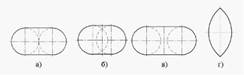
Закрытый тор показан на рисунке а) Самопересекающимся является тор, показан на рисунке б)

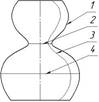
Главным меридианом поверхности вращения, показанной на чертеже, является линия 1

Экватором поверхности вращения, показанной на чертеже, является линия 4

Геликоидом называется винтовая поверхность, образующей которой является прямая

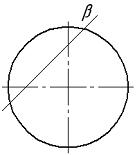
Плоскость β пересекает сферическую поверхность по окружности

Поверхность, образующаяся перемещением прямолинейной образующей l по ломаной направляющей m, называется гранной поверхностью

Коническая поверхность пересекается по параболе плоскостьюβ