Теория фильтрования с образованием осадка

Основной задачей теории фильтрования является определение скорости фильтрования в зависимости от различных факторов, влияющих на этот процесс. Скорость фильтрования 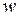– это объем 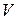профильтрованной в единицу времени 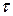жидкости, отнесенной к единице фильтрующей поверхности 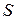. Очевидно:

Скорость фильтрования – сложная функция ряда факторов: структуры и толщины слоя осадка, формы фильтра, вязкости жидкости, перепада давлений.

Теория фильтрования основана на предположении о ламинарном характере движения жидкости в капиллярах. Это предположение вытекает из того, что диаметр пор осадка очень мал, поэтому число Рейнольдса будет меньше критического значения. Отсюда следует, что движение жидкости в капиллярах фильтра может быть описано уравнением Пуазейля:

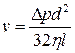
где 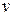– скорость движения жидкости в капилляре; 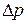– перепад давлений ( 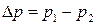, рис. 112); 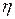- динамическая вязкость жидкости; 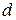– диаметр капилляра; 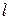– длина капилляра.

Рис. 112. Схема фильтрования с образованием осадка

Расход жидкости 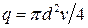через один капилляр или:

,

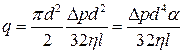где 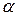- величина, зависящая от формы капилляра (для капилляра круглого сечения ).

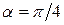Если площадь фильтрования 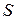, а число пор на единице площади 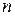, то за время 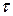протечет объем жидкости:

.

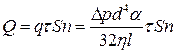Выразим длину капилляра через толщину фильтрующего слоя:

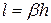
где 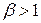– коэффициент криволинейности капилляра.

Число капилляров 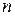на единице поверхности зависит от размера частиц осадка:

,

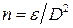где 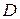– диаметр частицы; 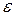- коэффициент пропорциональности.

С величиной 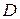связан также диаметр капилляра:

,

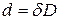где 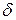- коэффициент, зависящий от взаимного расположения частиц осадка.

Из уравнения , подставляя в него уравнения – получим:

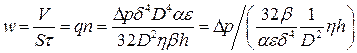
Безразмерный комплекс 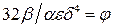характеризует структуру осадка.

Величина 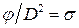называется структурным сопротивлением фильтрованию.

То, что величина 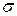является сопротивлением фильтрованию, следует из ее нахождения в знаменателе уравнения. Это сопротивление зависит от структуры осадка:

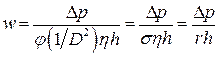
Величина 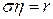называется удельным сопротивлением (размерность ).

В уравнении не учтено сопротивление фильтрующей перегородки. Обозначим его 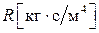. Тогда:

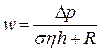
Уравнение выведено при условии, что все величины, характеризующие структуру осадка, неизменны. Следовательно, оно применимо только для несжимаемых осадков с одинаковой укладкой частиц по всей глубине.

Полное уравнение, учитывающее сжимаемость осадка (уравнение Знаменского), принимает вид:

,

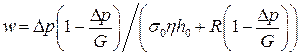где 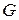– модуль сжатия осадка, Па; 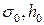– структурное сопротивление и толщина слоя осадка при нормальном давлении, например, равном давлению столба суспензии высотой 1м.

Из уравнения следует, что скорость фильтрования: 1) при сжимаемых осадках не пропорциональна давлению; 2) обратно пропорциональна толщине слоя осадка; 3) уменьшается с увеличением вязкости.