Сферический маятник
Были проанализированы сложные динамические процессы в сферическом маятнике с двумя степенями свободы. В численных экспериментах им найдены хаотические решения этой задачи, возникающие, когда точка подвеса совершает вынужденные периодические движения. Уравнения движения можно получить из лагранжиана, имеющего вид
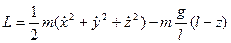 ,
,
где 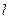 – длина маятника, а координаты
– длина маятника, а координаты 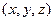 подчиняются связи
подчиняются связи
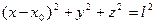 .
.
Координата точки подвеса есть 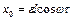 , а тяготение действует вдоль оси
, а тяготение действует вдоль оси 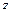 .
.
Используя методы теории возмущений, и т полученные уравнения движения преобразуется с помощью соотношений
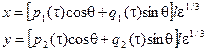
где 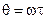 и
и 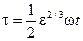 . В результате получается следующая система четырех уравнений первого порядка для
. В результате получается следующая система четырех уравнений первого порядка для 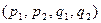 , в которую добавлено слабое затухание (описываемое коэффициентом
, в которую добавлено слабое затухание (описываемое коэффициентом 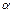 ):
):
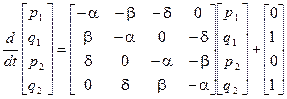
где 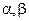 и
и  зависят от переменных
зависят от переменных 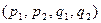 . Точки равновесия системы уравнений соответствуют периодическим плоским либо пространственным движениям. Численное решение этой системы уравнений обнаруживает переход от замкнутых орбит и дискретных спектров к сложным орбитам и широким спектрам, характерным для хаотического движения.
. Точки равновесия системы уравнений соответствуют периодическим плоским либо пространственным движениям. Численное решение этой системы уравнений обнаруживает переход от замкнутых орбит и дискретных спектров к сложным орбитам и широким спектрам, характерным для хаотического движения.
