Линейная регрессия и корреляция.

Рассмотрим простейшую модель парной регрессии – линейную регрессию. Модель линейной регрессии является наиболее распространенным и простым видом зависимости между экономическими переменными. Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров.

Линейная парная регрессия сводится к нахождению уравнения вида

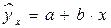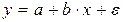или , (1)

где a и b – параметры модели, e - случайная величина (величина остатка).

Уравнение вида (1) позволяет по заданным значениям фактора х находить теоретические значения результативного признака, подставляя в него фактические значения фактора х.

Построение линейной регрессии сводится к оценке ее параметров – а и b. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических 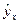минимальна:

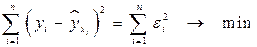. (2)

Т.е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 2):

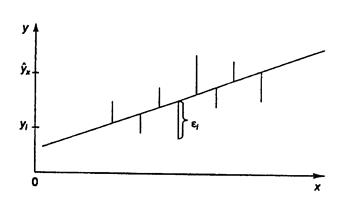
Рис. 2. Линия регрессии с минимальной дисперсией остатков.

Как известно из курса математического анализа, чтобы найти минимум функции (2), надо вычислить частные производные по каждому из параметров а и b и приравнять их к нулю. Обозначим 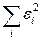через 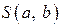, тогда:

.

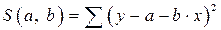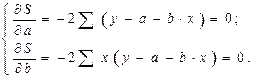(3)

После несложных преобразований, получим следующую систему линейных уравнений для оценки параметров а и b:

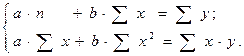(4)

Решая систему уравнений, найдем искомые оценки параметров а и b. Можно воспользоваться формулами Крамера

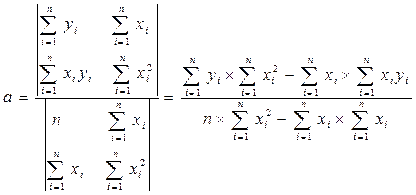
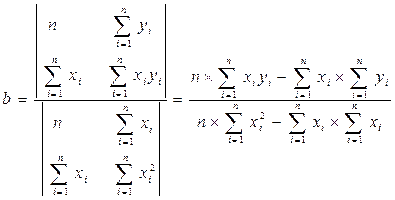
или следующими готовыми формулами:

, ,

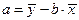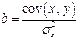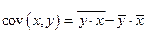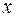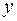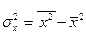где – ковариация признаков и , – дисперсия признака 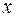и

, , , .

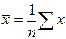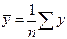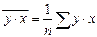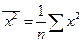Ковариация – числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий. Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности.

Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.

Формально a – значение y при x=0. Если признак-фактор x не может иметь нулевого значения, то вышеуказанная трактовка свободного члена a не имеет смысла, т.е. параметр a может не иметь экономического содержания.

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции 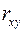, который можно рассчитать по следующим формулам:

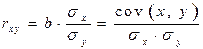. (6)

Линейный коэффициент корреляции находится в пределах: 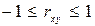. Чем ближе абсолютное значение 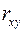к единице, тем сильнее линейная связь между факторами (при 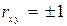имеем строгую функциональную зависимость). Но следует иметь в виду, что близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции 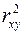, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака 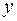, объясняемую регрессией, в общей дисперсии результативного признака:

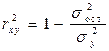, (7)

где , .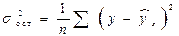

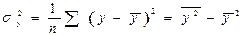Соответственно величина 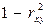характеризует долю дисперсии 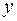, вызванную влиянием остальных, не учтенных в модели, факторов.

После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:

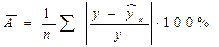. (8)

Средняя ошибка аппроксимации не должна превышать 8–10%.

Оценка значимости уравнения регрессии в целом производится на основе 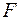-критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели.

Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной 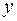от среднего значения 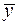раскладывается на две части – «объясненную» и «необъясненную»:

,

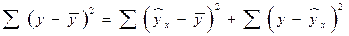где 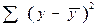– общая сумма квадратов отклонений; 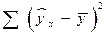– сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений); 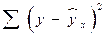– остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов.

Схема дисперсионного анализа имеет вид, представленный в таблице 1 ( 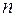– число наблюдений, 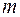– число параметров при переменной ).

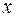Таблица 1

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Дисперсия на одну степень свободы
Общая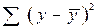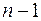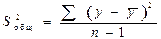
Факторная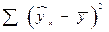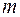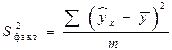
Остаточная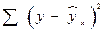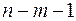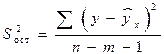

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину 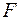-критерия Фишера:

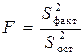. (9)

Фактическое значение 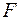-критерия Фишера (1.9) сравнивается с табличным значением 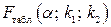при уровне значимости 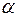и степенях свободы 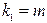и 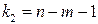. При этом, если фактическое значение 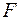-критерия больше табличного, то признается статистическая значимость уравнения в целом.

Для парной линейной регрессии 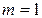, поэтому

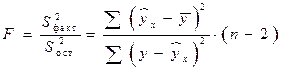. (10)

Величина 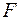-критерия связана с коэффициентом детерминации 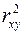, и ее можно рассчитать по следующей формуле:

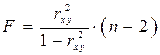. (11)

В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: 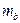и .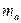

Стандартная ошибка коэффициента регрессии определяется по формуле:

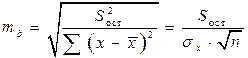, (12)

где 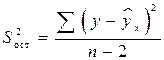– остаточная дисперсия на одну степень свободы.

Величина стандартной ошибки совместно с t-распределением Стьюдента при n-2 степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала.

Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t-критерия Стьюдента: 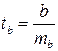которое затем сравнивается с табличным значением при определенном уровне значимости α и числе степеней свободы n-2. Доверительный интервал для коэффициента регрессии определяется как 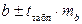. Поскольку знак коэффициента регрессии указывает на рост результативного признака 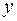при увеличении признака-фактора x ( 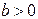), уменьшение результативного признака при увеличении признака-фактора ( 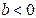) или его независимость от независимой переменной ( 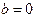) (см. рис. 1.3), то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, 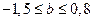. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.

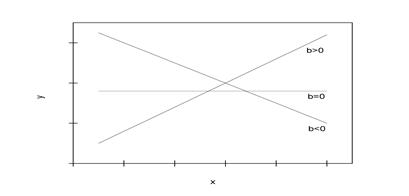
Рис. 3. Наклон линии регрессии в зависимости от значения параметра .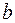

Стандартная ошибка параметра a определяется по формуле:

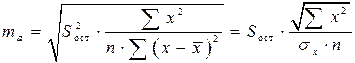. (13)

Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии. Вычисляется t-критерий: 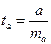, его величина сравнивается с табличным значением при n-2 степенях свободы.

Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции :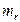

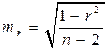. (14)

Фактическое значение t-критерия Стьюдента определяется как .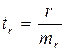

Существует связь между t-критерием Стьюдента и F-критерием Фишера:

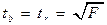. (15)

В прогнозных расчетах по уравнению регрессии определяется предсказываемое 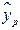значение как точечный прогноз 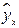при 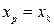, т.е. путем подстановки в уравнение регрессии 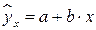соответствующего значения x. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки 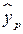, т.е. 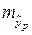, и соответственно интервальной оценкой прогнозного значения : ,

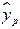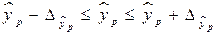где 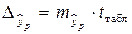, а 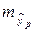– средняя ошибка прогнозируемого индивидуального значения:

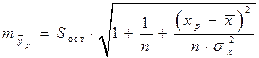. (16)