Критерий фишера

Для сравнения двух нормально распределенных совокупностей, у которых нет различий в средних выборочных значениях, но есть разница в дисперсиях, используют критерий Фишера. Фактический критерий рассчитывают по формуле:

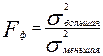
где в числителе стоит большее значение выборочной дисперсии, а в знаменателе - меньшее. Для вывода о достоверности различий между выборками используют ОСНОВНОЙ ПРИНЦИП проверки статистических гипотез. Критические точки для 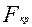содержатся в таблице. Нулевую гипотезу отвергают, если фактически установленная величина 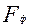превзойдет или окажется равной критическому (стандартному) значению 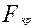этой величины для принятого уровня значимости a и числа степеней свободы k₁=n_{большая}-1; k₂=n_{меньшая}-1.

П р и м е р: при изучении влияния некоторого препарата на скорость проростания семян было установлено, что в экспериментальной партии семян и контроле средняя скорость проростания одинакова, но есть разница в дисперсиях. 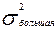=1250, 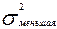= 417. Объемы выборок одинаковы и равны 20.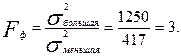 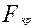= 2,12. Следовательно, нулевая гипотеза отвергается.