Линейная зависимость строк и столбцов матрицы
Умножение матриц.
Определение. Произведением матрицы 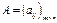 размеров
размеров 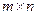 на матрицу
на матрицу 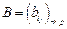 размеров
размеров 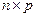 называется матрица
называется матрица 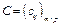 размеров
размеров 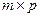 , элементы которой определяются следующим образом:
, элементы которой определяются следующим образом:
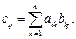
Теорема. (Свойства операции умножения матриц)
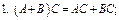
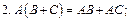
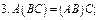
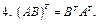
Теорема. (Об умножении квадратной матрицы на единичную матрицу)
Умножение всякой квадратной матрицы на единичную матрицу того же размера слева или справа не меняет исходную матрицу.
4.3.4. Теорема. (Об умножении квадратной матрицы на скалярную матрицу)
Пусть 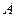 − квадратная матрица размера
− квадратная матрица размера 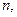 а
а 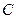 − скалярная матрица того же размера. Тогда
− скалярная матрица того же размера. Тогда 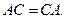
4.3.5. Теорема. (Об умножении диагональных матриц)
Пусть 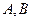 − диагональные квадратные матрицы размера
− диагональные квадратные матрицы размера 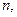 тогда
тогда 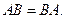
4.3.6. Теорема. (Об определителе произведения квадратных матриц)
Определитель произведения квадратных матриц равен произведению определителей этих матриц.
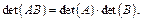
Обратная матрица
Определение. Пусть 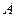 − квадратная матрица размера
− квадратная матрица размера 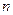 ,
, 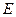 − единичная матрица того же размера. Матрица
− единичная матрица того же размера. Матрица 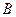 называется левой обратной по отношению к
называется левой обратной по отношению к 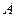 , если
, если 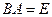 . Матрица
. Матрица 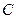 называется правой обратной по отношению к
называется правой обратной по отношению к 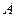 , если
, если 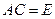 .
.
4.7.2. Теорема. (О единственности обратной матрицы)
Если для квадратной матрицы 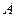 существуют ее левая и правая обратные матрицы, то они совпадают.
существуют ее левая и правая обратные матрицы, то они совпадают.
Доказательство:
Пусть 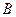 − правая, а
− правая, а 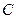 − левая обратные матрицы для матрицы. Тогда
− левая обратные матрицы для матрицы. Тогда
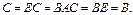
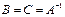 . Таким образом, матрица
. Таким образом, матрица 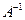 называется обратной по отношению к матрице
называется обратной по отношению к матрице 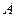 , если
, если 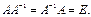
4.7.5. Теорема. (Критерий существования обратной матрицы)
Для того, чтобы квадратная матрица 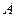 была обратимой, необходимо и достаточно, чтобы она была невырожденной.
была обратимой, необходимо и достаточно, чтобы она была невырожденной.
Доказательство: Необходимость.
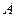 обратима, следовательно, существует
обратима, следовательно, существует 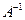 . по теореме об определителе произведения квадратных матриц
. по теореме об определителе произведения квадратных матриц
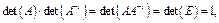
следовательно, 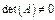 , то есть матрица
, то есть матрица 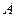 является невырожденной.
является невырожденной.
Достаточность.
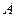 является невырожденной, то есть
является невырожденной, то есть 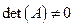 .
. 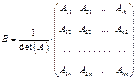 , (4.1)
, (4.1)
где 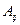 − алгебраическое дополнение элемента
− алгебраическое дополнение элемента 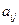 матрицы
матрицы 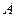 . Рассмотрим их произведение
. Рассмотрим их произведение 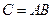 :
:
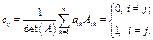
Следовательно, произведение матрицы 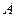 на
на 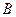 равно единичной матрице. Аналогично показывается, что произведение матрицы
равно единичной матрице. Аналогично показывается, что произведение матрицы 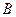 на
на 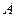 есть единичная матрица, а это означает, что матрица
есть единичная матрица, а это означает, что матрица 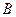 является обратной по отношению к матрице
является обратной по отношению к матрице 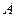 .
.
Теорема доказана.
Определение. Матрица, являющаяся транспонированной по отношению к матрице, составленной из алгебраических дополнений соответствующих элементов матрицы 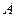 , называется присоединенной для матрицы
, называется присоединенной для матрицы 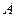 и обозначается
и обозначается 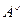 .
.
Замечание. Метод нахождения обратной матрицы с помощью формулы (1) называется методом присоединенной матрицы.
Пример.
Найдем обратную матрицу для матрицы
1)det(A)не=0
2)А*
3)А =
4.7.7. Теорема. (Об обратной матрице произведения матриц)
Матрица, обратная произведению двух матриц, равна произведению их обратных матриц, взятых в обратном порядке:
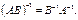
Доказательство:
Пусть 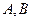 − невырожденные квадратные матрицы одного порядка. Тогда по теореме 4.3.6 об определителе произведения квадратных матриц их произведение
− невырожденные квадратные матрицы одного порядка. Тогда по теореме 4.3.6 об определителе произведения квадратных матриц их произведение 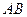 также является невырожденной матрицей. Следовательно, по теореме 4.7.5 существуют обратные матрицы
также является невырожденной матрицей. Следовательно, по теореме 4.7.5 существуют обратные матрицы 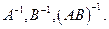
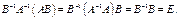
Аналогично
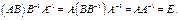
Следовательно, матрица 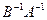 является обратной по отношению к произведению матриц
является обратной по отношению к произведению матриц 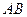 .
.
Нахождение обратной матрицы с помощью элементарных преобразований.
Обратную матрицу можно также найти с помощью элементарных преобразований строк исходной матрицы 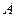 . Для этого требуется составить блочную матрицу
. Для этого требуется составить блочную матрицу 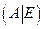 , а затем с помощью элементарных преобразований строк привести эту блочную матрицу к виду
, а затем с помощью элементарных преобразований строк привести эту блочную матрицу к виду 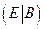 . Полученная матрица
. Полученная матрица 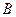 и будет обратной по отношении к матрице
и будет обратной по отношении к матрице 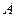 .
.
4.7.10. Решение матричных уравнений.
Рассмотрим основные виды матричных уравнений:
1) 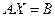 , 2)
, 2) 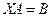 ,
,
где 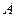 − квадратная невырожденная матрица.Решением матричного уравнения называется такая матрица
− квадратная невырожденная матрица.Решением матричного уравнения называется такая матрица 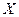 , которая при подстановке в матричное уравнение обращает его в тождество.
, которая при подстановке в матричное уравнение обращает его в тождество.
Умножим обе части уравнения
1) 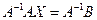 ,
,
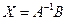 .
.
2) 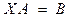
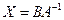 .
.
.
Формулы Крамера.
Обозначим 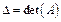 и запишем решение (4.3) в явном виде:
и запишем решение (4.3) в явном виде:
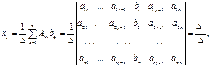
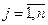 .
.
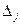 - определитель, у которого столбец
- определитель, у которого столбец 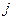 заменен на столбец свободных членов системы.
заменен на столбец свободных членов системы.
Замечание. формулы Крамера применимы лишь для СЛАУ в случае невырожденной матрицы 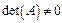 .
.
Линейная зависимость строк и столбцов матрицы.
Определение. Строка 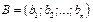 называется линейной комбинацией строк
называется линейной комбинацией строк 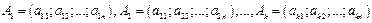 с коэффициентами
с коэффициентами 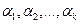 , если для всех элементов этой строки справедливо равенство:
, если для всех элементов этой строки справедливо равенство:
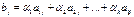 ,
, 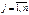 .
.
4.8.2. Определение.
Строки 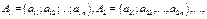
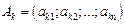 называются линейно зависимыми, если существует их нетривиальная линейная комбинация, равная нулевой строке, т.е. существуют такие не все равные нулю числа
называются линейно зависимыми, если существует их нетривиальная линейная комбинация, равная нулевой строке, т.е. существуют такие не все равные нулю числа
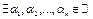
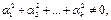
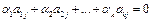 ,
, 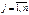 .
.
4.8.3. Определение.
Строки 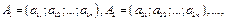
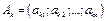 называются линейно независимыми, если только их тривиальная линейная комбинация равна нулевой строке, т.е.
называются линейно независимыми, если только их тривиальная линейная комбинация равна нулевой строке, т.е.
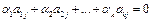 ,
, 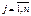
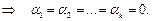
4.8.4. Теорема. (Критерий линейной зависимости строк матрицы)
Для того, чтобы строки 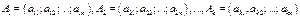 были линейно зависимыми, необходимо и достаточно, чтобы хотя бы одна из них была линейной комбинацией остальных.
были линейно зависимыми, необходимо и достаточно, чтобы хотя бы одна из них была линейной комбинацией остальных.
Доказательство:
Необходимость. Пусть строки 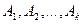 линейно зависимы, тогда существует их нетривиальная линейная комбинация, равная нулевой строке:
линейно зависимы, тогда существует их нетривиальная линейная комбинация, равная нулевой строке:
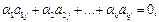
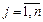 .
.
Без ограничения общности предположим, что первый из коэффициентов линейной комбинации отличен от нуля .
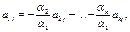
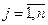 ,
,
то есть первая строка является линейной комбинацией остальных.
Достаточность. Пусть одна из строк, например, 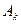 , является линейной комбинацией остальных, тогда
, является линейной комбинацией остальных, тогда
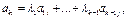
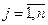
то есть существует нетривиальная линейная комбинация строк 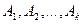 , равная нулевой строке:
, равная нулевой строке:
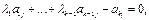
а значит, строки 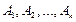 линейно зависимы, что и требовалось доказать.
линейно зависимы, что и требовалось доказать.
Замечание.
Аналогичные определения и утверждения могут быть сформулированы и для столбцов матрицы.
§4.9. Ранг матрицы.
4.9.1. Определение. Минором порядка 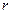 матрицы
матрицы 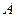 размера
размера 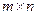 называется определитель порядка
называется определитель порядка 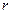 с элементами, расположенными на пересечении некоторых ее
с элементами, расположенными на пересечении некоторых ее 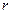 строк и
строк и 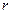 столбцов.
столбцов.
Определение. Отличный от нуля минор порядка 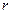 матрицы
матрицы 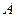 размера
размера 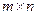 называется базисным минором, если все миноры матрицы порядка
называется базисным минором, если все миноры матрицы порядка 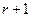 равны нулю.
равны нулю.
4.9.4. Определение. Рангомматрицы называется порядок ее базисного минора. 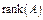 или
или 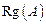 .
.
Теорема.(Инвариантность ранга матрицы относительно элементарных преобразований)
Ранг матрицы не меняется при ее элементарных преобразованиях.
Без доказательства.
4.9.6. Теорема. (О базисном миноре).
Базисные строки (столбцы) линейно независимы. Всякая строка (столбец) матрицы может быть представлена в виде линейной комбинации ее базисных строк (столбцов).
Доказательство: (для строк)
Пусть ранг матрицы 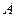 размеров
размеров 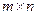 равен
равен 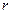 , а
, а 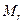 − базисный минор. Без ограничения на общность предположим, что базисный минор расположен в левом верхнем углу:
− базисный минор. Без ограничения на общность предположим, что базисный минор расположен в левом верхнем углу:
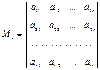 .
.
1) Предположим, что базисные строки линейно зависимы. Тогда согласно теореме «Критерий линейной зависимости строк матрицы» одна из строк может быть представлена в виде линейной комбинации остальных базисных строк. Следовательно, если вычесть из этой строки указанную линейную комбинацию, то мы получим нулевую строку, а это означает, что минор 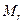 равен нулю, что противоречит определению базисного минора. Следовательно, линейная независимость базисных строк доказана.
равен нулю, что противоречит определению базисного минора. Следовательно, линейная независимость базисных строк доказана.
2) Если номер рассматриваемой строки 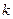 от 1 до r, то тогда, очевидно, она может быть представлена в виде линейной комбинации c коэффициентом, равным 1 при строке
от 1 до r, то тогда, очевидно, она может быть представлена в виде линейной комбинации c коэффициентом, равным 1 при строке 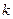 и нулевыми коэффициентами при остальных строках. Покажем теперь, что если номер строки
и нулевыми коэффициентами при остальных строках. Покажем теперь, что если номер строки 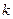 от
от 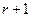 до
до 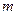 , она может быть представлена в виде линейной комбинации базисных строк. Рассмотрим минор матрицы
, она может быть представлена в виде линейной комбинации базисных строк. Рассмотрим минор матрицы 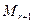 ,
,
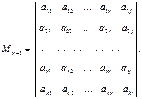
Если номер столбца 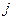 от 1 до r, то имеем определитель с двумя одинаковыми столбцами, который, очевидно, равен нулю. Если же номер столбца
от 1 до r, то имеем определитель с двумя одинаковыми столбцами, который, очевидно, равен нулю. Если же номер столбца 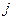 от r+1 до
от r+1 до 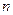 , а номер строки
, а номер строки 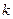 от
от 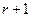 до
до 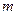 , то
, то 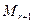 является минором исходной матрицы большего порядка, чем базисный минор, а это означает, что он равен нулю из определения базисного минора. Таким образом, доказано, что минор
является минором исходной матрицы большего порядка, чем базисный минор, а это означает, что он равен нулю из определения базисного минора. Таким образом, доказано, что минор 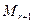 равен нулю для любого номера строки
равен нулю для любого номера строки 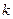 от
от 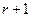 до
до 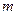 и для любого номера столбца
и для любого номера столбца 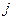 от 1 до
от 1 до 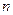 . Разлагая его по последнему столбцу, получим:
. Разлагая его по последнему столбцу, получим:
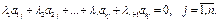
Здесь 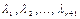 − соответствующие алгебраические дополнения. Заметим, что
− соответствующие алгебраические дополнения. Заметим, что 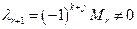 , так как следовательно,
, так как следовательно, 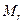 является базисным минором. Следовательно, элементы строки k могут быть представлены в виде линейной комбинации соответствующих элементов базисных строк с коэффициентами, не зависящими от номера столбца
является базисным минором. Следовательно, элементы строки k могут быть представлены в виде линейной комбинации соответствующих элементов базисных строк с коэффициентами, не зависящими от номера столбца 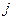 :
:
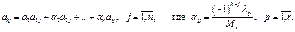
Таким образом, мы доказали, что произвольная строка матрицы может быть представлена в виде линейной комбинации ее базисных строк. Теорема доказана.
4.9.8. Метод окаймляющих миноров для нахождения ранга матрицы.
Определение. Минор 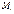 называется окаймляющим по отношению к минору
называется окаймляющим по отношению к минору 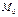 , если он получен из минора
, если он получен из минора 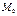 добавлением одной новой строки и одного нового столбца исходной матрицы.
добавлением одной новой строки и одного нового столбца исходной матрицы.
4.9.8.2. Процедура нахождения ранга матрицы методом окаймляющих миноров.
1. Находим какой-либо текущий минор матрицы отличный от нуля.
2. Вычисляем все окаймляющие его миноры.
3. Если все они равны нулю, то текущий минор является базисным, и ранг матрицы равен порядку текущего минора.
4. Если среди окаймляющих миноров находится хотя бы один отличный от нуля, то он полагается текущим и процедура продолжается.
4.9.9. Нахождение ранга матрицы методом элементарных преобразований.
На основании теоремы «Инвариантность ранга матрицы относительно элементарных преобразований» можно утверждать, что ранг матрицы не меняется при элементарных преобразованиях (то есть ранги эквивалентных матриц равны). Поэтому ранг матрицы равен рангу ступенчатой матрицы, полученной из исходной элементарными преобразованиями. Ранг же ступенчатой матрицы, очевидно, равен количеству ее ненулевых строк.
