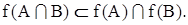Образи і прообрази

У загальному випадку при відображенні 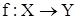елемент із Y може бути образом не одного, а декількох елементів множині X. Так, для розглянутого в 1.3.1 відношення елемент 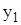є образом елементів 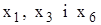. Сукупність всіх елементів, образом яких є даний елемент у з Y, називається повним прообразом елемента у і позначається 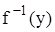. У нашому прикладі .

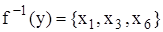Нехай Q — деяка підмножина множині X, на якій визначене відображення f. Сукупність елементів f(q), що є образами всіх елементів множині Q, називається образом цієї множині і позначається f(Q). У свою чергу, для кожної множині R із Y визначається його повний прообраз 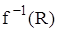як сукупність усіх тих елементів із X, образи яких належать R.

Основні властивості відображень виражаються співвідношеннями:

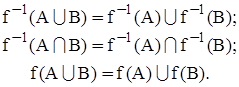
Образ перетинання двох множин, узагалі говорячи, не збігається з перетинанням їхніх образів. Але можна показати, що