Быстрое преобразование Фурье в базисах Уолша
ДПФ в базисе дискретных экспоненциальных функций (ДЭФ) предполагает выполнение большого числа комплексных умножений, требующих существенных затрат машинного времени, что ограничивает возможность его практического применения. Существует широкий класс систем базисных функций, в которых преобразование Фурье сводится к алгебраическим преобразованиям над дискретными отсчетами. К такому классу относятся функции Уолша. Наибольшее применение нашли функции Уолша, Уолша-Адамара, Уолша-Пели.
Рассмотрим ДПФ в базисе функций Уолша-Адамара.
Базис Уолша-Адамара вводится посредством т.н. матриц Адамара, которые строятся на основании следующего рекуррентного правила
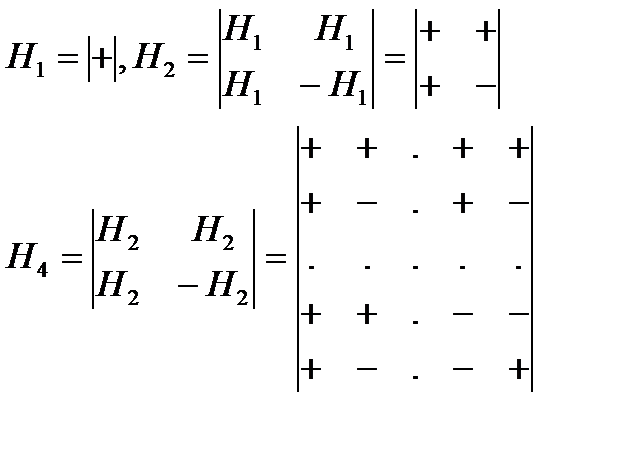
Обозначая через 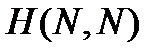 матрицу Адамара размерности
матрицу Адамара размерности 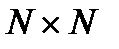 , дискретный спектр можно записать в матричной форме следующим образом
, дискретный спектр можно записать в матричной форме следующим образом
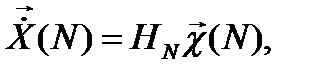
(4.10)
где 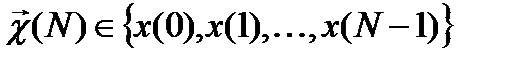 -вектор-столбец входного сигнала,
-вектор-столбец входного сигнала,
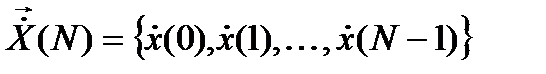 -вектор-строка дискретного спектра.
-вектор-строка дискретного спектра.
Поведем вычисления 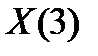 в базисе Уолша-Адамара для
в базисе Уолша-Адамара для 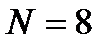 .
.
Составим матрицу Адамара 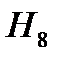
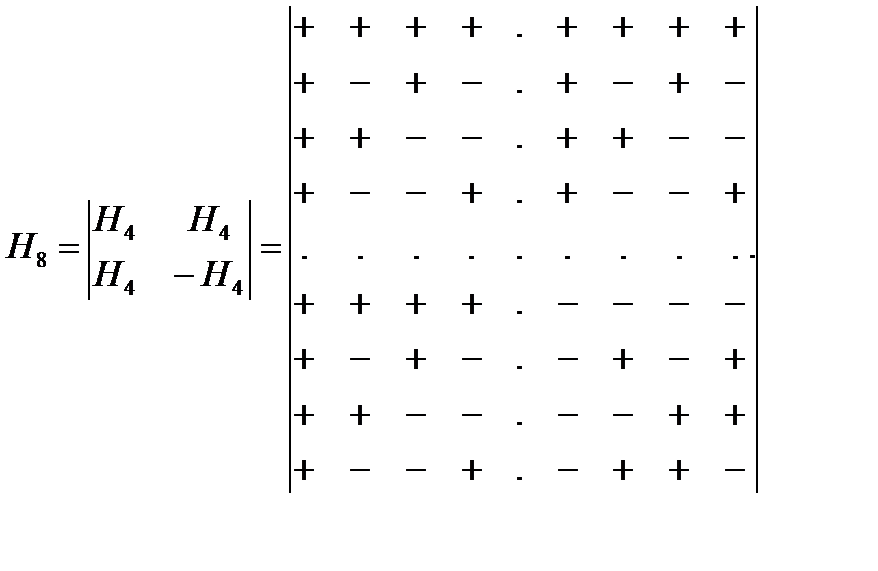
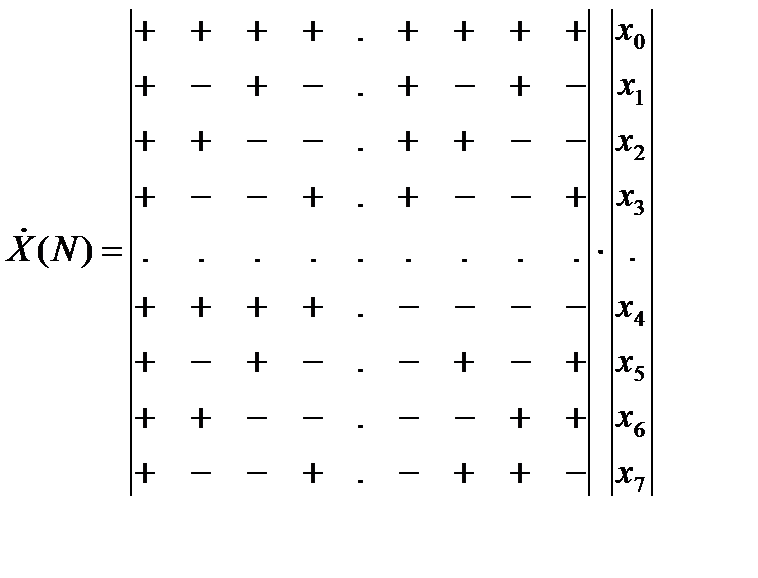
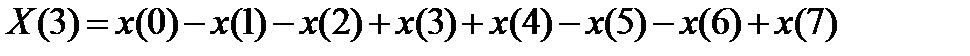
Легко убедится в том, что к матрице Адамара можно прийти полагая в дереве БПФ все весовые коэффициенты ребер графа равны 1.
Операция “бабочка” сводится к вычислениям
т.е. процессор Фурье в базисе Уолша-Адамара вычисляет дискретный спектр используя лишь простейшие арифметические операции суммирования и вычитания отсчетов сигнала.
На ряду с базисом Уолша-Адамара существуют базис Уолша-Пели и классический базис Уолша.
