Производная сложной функции. Полная производная. Полный дифференциал сложной функции.

Лекция 12.

Предположим, что в уравнении z=F(u,v) (1) u,v - функции независимых переменных x,y:

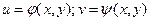(2)

В этом случае z есть сложная функция от аргументов x,y.

В общем случае z можно выразить через x,y непосредственно, а именно:

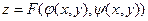(3)

Пример 1 .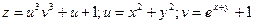

Тогда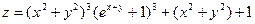

Предположим, что 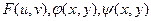имеют непрерывные частные производные по всем своим аргументам.

Задача. Вычислить 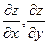исходя из уравнений (1),(2), не пользуясь уравнением (3).

Даем аргументу x приращение 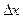, оставляя y неизменной, тогда u,v получают приращения 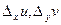. Но если u,v получают приращения 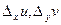, то и функция z=F(u,v) получит приращение 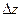, определяемое следующей формулой:

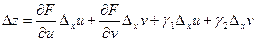
Разделим обе части равенства на :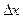

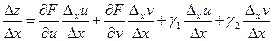
Если 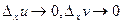(в силу непрерывности функций u,v), то 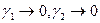. Переходя к пределу при 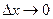получим 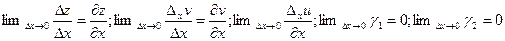. Следовательно

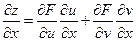(4) аналогично 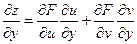(4’)

Пример 2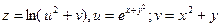

Решение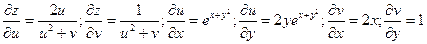

Используя формулы (4),(4’) получаем

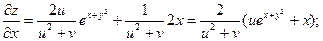
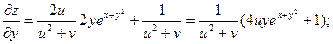
В последнем выражении вместо u,v можно подставить их выражения.

Для случая большего числа переменных формулы (4),(4’) обобщаются.

Например, для w=F(z,u,v,s), которая является функцией 4-ч переменных, и каждая их которых зависит от переменных x,y, то формула (4),(4’) принимает вид:

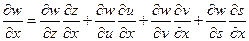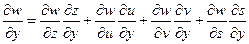и (5)

Если задана функция z=F(x,y,u,v), где y,u,v - в свою очередь зависят от одного аргумента x 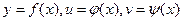, то по сути z - функция от одного аргумента. Тогда можно рассмотреть вопрос о нахождении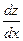

Эта производная вычисляется по первой из формул (5), то есть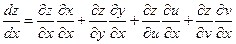

Но так как y,u,v – функции только одного переменного x, то частные производные обращаются в обыкновенные, и кроме того 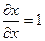, поэтому 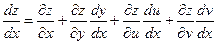. Это формула для вычисления полной производной 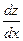(в отличие от частной производной )

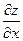Пример 3

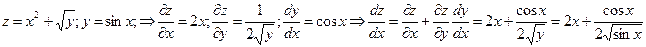
Найдем полный дифференциал сложной функции, определенной равенствами (1),(2).

Формула полного дифференциала 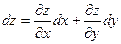(6)

Подставляя выражения 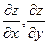, определенные равенствами (4),(4’) получим

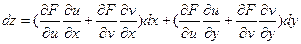Выполнив преобразование в правой части, получим

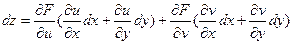(7) Но так как 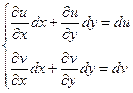(8), то равенство (7) с учетом равенства (8) можно переписать так: 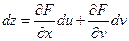(9) или 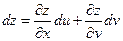(9’)

Сравнивая (6) и (9’) , можно сказать, что выражение полного дифференциала функции нескольких переменных (дифференциала первого порядка) имеет тот же вид, то есть форма дифференциала инвариантна, являются ли u,v независимыми переменными или функциями независимых переменных.

Пример. Найти полный дифференциал сложной функции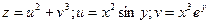

РешениеПо формуле (9’)

имеем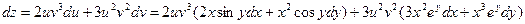

Последнее выражение можно переписать в виде

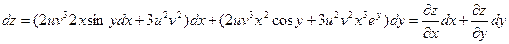
Производная от функции заданной неявно

Начнем рассмотрение этого вопроса с неявной функции одного переменного. Пусть некоторая функция определена уравнением

F(x,y)=0

Теорема. Пусть непрерывная функция y от x задана уравнением (1), где 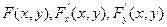- непрерывные функции в некоторой области D, содержащей точку (x,y), координаты которой удовлетворяют уравнению (1); кроме того, в этой точке 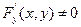. Тогда функция y от x имеет производную

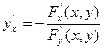(2)

Доказательство

Пусть некоторому значению x соответствует значение функции y при этом F(x,y)=0

Для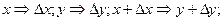

В силу 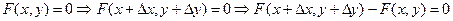. Это можно записать в виде

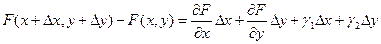, где при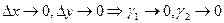

Так как левая часть равенства равна 0, то 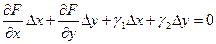. Делим на 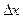и вычисляем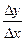

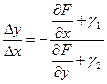
Пр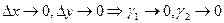и и 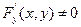,то в пределе получим 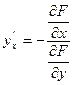(2’)

Доказано существование 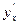от функции, заданной неявно, нашли формулу для ее вычисления.

Пример 1 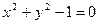- неявная функция.

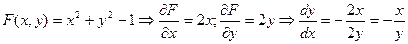
Пример 2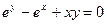

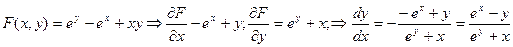
Рассмотрим уравнение вида F(x,y,z)=0 (3)

Если каждой паре x и y из некоторой области соответствует одно или несколько значений z, удовлетворяющих уравнению (3), то это уравнение неявно определяет одну или несколько однозначных функций z от x,y.

Например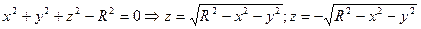

Для 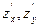имеют место формулы 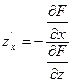и 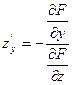. Предполагается, что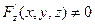

Аналогичным образом определяются неявные функции любого числа переменных и находятся их частные производные.

Пример 3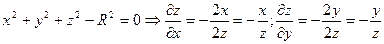

Дифференцируя эту функцию как явную (после разрешения уравнения относительно z) получили бы тот же результат

Пример 4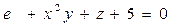

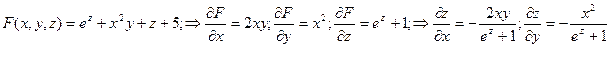
Частные производные различных порядков

Рассмотрим функцию z=f(x,y). 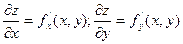- функции переменных x,y, от которых можно снова находить частные производные. Частных производных второго порядка от функций двух переменных четыре, так как каждую из функций 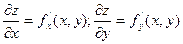можно дифференцировать как по x, так и по y.

Обозначение

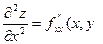- последовательное дифференцирование по x.

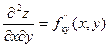- последовательное дифференцирование по x, затем по y.

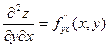- последовательное дифференцирование по y, затем по x.

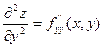- последовательное дифференцирование по y.

Производные второго порядка можно снова дифференцировать как по x, так и по y. Получаем частные производные третьего порядка. Их будет восемь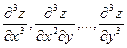

В общем случае частная производная n-го порядка есть первая производная от производной (n-1) порядка.

Формула 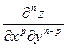- соответствует производной n-го порядка. Функция z сначала p раз дифференцируется по x, затем n-p раз по y.

Для функции любого числа переменных частные производные высших порядков определяются аналогично.

Пример 1 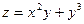. Найти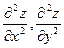

Решение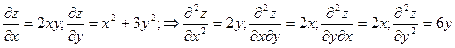

Пример 2 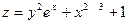. Найти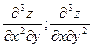

Решение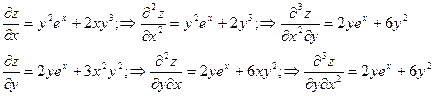

Пример 3 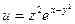. Найти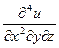

Решение