Кинематика прямолинейного движения

КИНЕМАТИКА

1. Средняя скорость V_ср

, ,

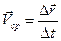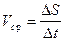где 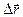- вектор перемещения, DS - путь, пройденный телом за время Dt.

2. Мгновенная скорость 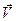и мгновенное ускорение 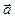прямолинейного движения в общем случае

, , .

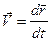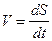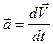3. Вектор полного ускорения

, ,

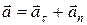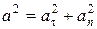где 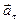- тангенциальное (касательное) ускорение, 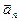- нормальное (центростремительное) ускорение

, ,

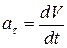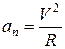где R - радиус кривизны траектории в данной точке.

4. В случае прямолинейного равномерного движения ( 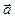=0)

V = S/t = const.

5. В случае прямолинейного равнопеременного движения ( )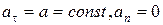

пройденный путь S и конечная скорость V определяются по формулам

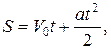
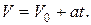
В этих уравнениях ускорение 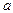положительно при равноускоренном движении и отрицательно - при равнозамедленном.

6. Мгновенная угловая скорость

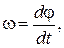
где j - угол поворота. В случае равномерного вращательного движения

w = j /t.

7. Мгновенное угловое ускорение

.

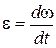8. В случае вращательного движения с постоянным угловым ускорением угол поворота и угловая скорость определяются уравнениями

j = j₀ + 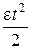, w = w₀ + e t.

9. Связь между линейными и угловыми величинами

dS = R dj; V = Rw; ;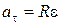

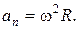
КИНЕМАТИКА ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ

1. Тело, брошенное вертикально вверх, вернулось на землю через 3 секунды. Какова была начальная скорость тела? На какую высоту поднялось тело? Сопротивлением воздуха пренебречь. (14,7 м/с,11 м)

2. Камень бросили вертикально вверх на высоту 10 м. Через какое время он упадет на землю? Во сколько раз увеличится высота подъема камня, если его начальную скорость увеличить вдвое? Сопротивлением воздуха пренебречь. (2,9 с, в 4 раза).

3. С аэростата, находящегося на высоте 300 м, упал камень. Через сколько времени камень достигнет земли, если

1)аэростат поднимается со скоростью 5 м/с;

2)аэростат опускается со скоростью 5 м/с;

3)аэростат неподвижен?

Сопротивлением воздуха пренебречь. (8,4 с, 7,3 с, 7,8 с).

4. Тело падает вертикально с высоты 19,6 м с нулевой начальной скоростью. Какой путь пройдет тело за первую 0,1 с своего движения и за последнюю 0,1 с своего движения? Сопротивлением воздуха пренебречь. (0,049 м, 1,9 м).

5. Свободно падающее тело в последнюю секунду своего падения проходит половину всего пути. Найти с какой высоты падает тело и продолжительность его падения. (56,6 м, 3,4 с).

6. Расстояние между двумя станциями 2 км. Первую половину этого расстояния поезд проходит равноускоренно, вторую - равнозамедленно. Максимальная скорость поезда 72 км/ч. Найти величину ускорения, считая его численно равным замедлению и время движения поезда между станциями. (0,2 м/с², 200 с).

7. Поезд движется со скоростью 36 км/ч. Если прекратить подачу энергии, то поезд, двигаясь равнозамедленно, останавливается через 20 секунд. Найти ускорение поезда и расстояние, на котором надо отключить подачу энергии. (-0,5 м/с², 100 м).

8. Вагон движется равнозамедленно с ускорением -0,5 м/с². Начальная скорость вагона 54 км/ч. Через какое время и на каком расстоянии от начальной точки вагон остановится? (30 с, 225 м).

9. Зависимость пройденного телом пути от времени задается уравнением

S = А + Bt + Ct² + Dt³ (A = 1 м. B = 2м/с, С= 0,1 м/с², D=0,03 м/с³ ).

Определить: 1) через сколько времени после начала движения ускорение тела будет равно 2 м/с²; 2) среднюю скорость тела за этот промежуток времени; 3) среднее ускорение тела за этот промежуток времени. (10 с, 6 м/с, 1,1 м/с²).

10. На некотором участке пути движение поезда описывается уравнением S = 0,5t + 0,15t²,

где путь выражен в метрах, время - в секундах. Определить скорость и ускорение поезда в начальный момент и в конце седьмой секунды, а также среднюю скорость за первые семь секунд движения. (а₁ = а₂= 0,3 м/с² , v₁ = 0,5 м/с, v₂ = 2,6 м/с, v_ср = 1,55 м/с).

11. Две материальные точки движутся вдоль оси X так что их координаты зависят от времени по законам

Х₁ = 10 - 2t + 3t² , Х₂ = -5 + 3t².

(Координаты Х в метрах, время t в секундах). Где находятся точки в начальный момент? Где и в какой момент времени они встретятся? Каковы скорости и ускорения материальных точек в начальный момент? (Х₁₀=10 м, Х₂₀=-5 м, Х = 163,8 м, t = 7,5 с, V₁₀ = -2 м/с,V₂₀= 0, а₁₀ = 6 м/с², а₂₀ = 6 м/с²).

12. При наборе высоты самолет летит по прямой, составляющей угол 30° с горизонтом. Зависимость пути самолета от времени выражается формулой

S = 10 + 2t + t² ,

(путь - в метрах, время - в секундах). Найти в момент времени 1 минута скорость, ускорение и проекции вектора скорости самолета на гори-зонтальное и вертикальное направления. (122 м/с, 2 м/с², 105,8 м/с; 61 м/с).

13. Материальная точка движется прямолинейно таким образом, что ее скорость изменяется по закону V = 10 - 2t + 3t² (время - в секундах). Определить, какой путь она пройдет за 5 секунд. Определить ускорение точки в момент времени 5 секунд. (150 м., 28 м/с²).

14. Начав тормозить, автомобиль двигался так, что зависимость его пути от времени имела вид

S = 12t - 2t³ ,

(путь - в метрах, время - в секундах). В какой момент времени автомобиль остановится? Каков его тормозной путь? Чему равна скорость в начале торможения?(1,4 с, 11,3 м, 12 м/с).

15. В течение 5 секунд автомобиль разгоняется от скорости 36 км/ч до 72 км/ч. Найти его ускорение, считая движение равноускоренным. Опре-делить расстояние, которое автомобиль пройдет за это время. (2 м/с², 75 м).

16. С крыши высокого здания вертикально вниз бросили два камня с интервалом 1 с. и нулевой начальной скоростью. На каком расстоянии друг от друга будут находиться камни, когда скорость второго камня станет равной 23 м/с? (28 м).

17. Вертолет взлетает вертикально с постоянной скоростью 8 м/с. На высоте 12 м над землей из окна вертолета выбрасывают груз. Через какое время груз упадет на землю? (2,58 с).

18. Камень пролетает мимо окна высотой 2,1 метра за 0,3 секунды. С какой высоты падает камень, если подоконник находится на расстоянии 1 м от земли? (4,66 м).

19. Игрушечная ракета, запущенная вертикально вверх, пролетает мимо окна высотой 2 м за 0,15 с. Подоконник окна находится на высоте 10 м над землей. Какова стартовая скорость ракеты и как высоко она взлетит? (19,8 м/с, 20 м).

20. Камень брошен с утеса вертикально вниз с нулевой начальной скоростью. Звук от его падения в море слышен через 3,5 с. Чему равна высота утеса, если скорость звука 330 м/с? (54,5 м)

21. Тело, брошенное вертикально вверх на Земле, взлетает на высоту 23 метра. На какую высоту взлетит такое же тело на Луне, где ускорение свободного падения в 6 раз меньше, чем на Земле? Начальная скорость тел одинакова. (138 м).

22. С вершины утеса высотой 65 м брошен вертикально вверх камень со скоростью 10 м/с. Через какое время камень достигнет основания утеса? Какова его скорость перед ударом о землю? (4,8 с, 37 м/с).

23. Камень брошен вертикально вверх со скоростью 17,5 м/с. С какой скоростью он будет двигаться на высоте 12 м? Через какое время камень будет находиться на этой высоте? Почему на второй вопрос имеются два ответа? (8,4 м/с, 0,93 с или 2,65 с).

24. Ускорение частицы, двигающейся прямолинейно, дается выражением

а = 17,5 t^3/2.

Найдите зависимость координаты частицы от времени, если в начальный момент времени координата и скорость частицы равны нулю.

25. Тело проходит последовательно с постоянным ускорением два одинаковых отрезка пути по 10 м. Найти ускорение тела и его скорость в начале первого отрезка, если первый отрезок пути пройден телом за 1,06 с, а второй - за 2,2 с. (-3 м/с², 11 м/с).

2. КИНЕМАТИКА ДВИЖЕНИЯ ПО КРИВОЛИНЕЙНОЙ ТРАЕКТОРИИ

26. С башни в горизонтальном направлении брошено тело с начальной скоростью 10 м/с. Пренебрегая сопротивлением воздуха, определить скорость тела и радиус кривизны траектории через 2 секунды после начала движения. (22 м/с; 109 м.)

27. Мальчик бросает мяч вверх под углом 70° к горизонту и попадает прямо в открытое окно, которое расположено на 9,6 м выше его плеча. Мяч влетает в окно горизонтально. Определить радиус кривизны траектории мяча в момент, когда он перелетает через подоконник и начальную скорость мяча. (2,54 м; 14,6 м/с)

28. Тело брошено горизонтально с некоторой высоты. Найти зависимость от времени скорости, тангенциального и нормального ускорений тела.

29. С башни высотой 25 м бросили камень со скоростью 15 м/с под углом 30° к горизонту. На каком расстоянии от основания башни камень упадет на землю? В какой момент времени после начала движения нормальное ускорение камня будет равно ускорению силы тяжести? (41 м, 0,77 с).

30. Мальчик бросает мяч со скоростью 10 м/с под углом 45° к горизонту. Мяч ударяется о стенку, находящуюся на расстоянии 3 м от мальчика. Найти скорость мяча в момент удара. Какой угол составляет вектор скорости мяча в момент удара с радиусом кривизны траектории? (7,6 м/с).

31. Камень, брошенный горизонтально с некоторой высоты, упал на землю через 0,5 с на расстоянии 5 м по горизонтали от места бросания. Какой угол составляет скорость камня с горизонтом в точке его падения на землю? Чему равны его нормальное и тангенциальное ускорения в этой точке? (26°; 8,8 м/с²; 4,3 м/с²).

32. Два тела брошены с одинаковыми начальными скоростями под углами 30° и 60° к горизонту. Определить отношение максимальных высот подъема этих тел, отношение их дальностей полета и радиусов кривизны траектории в точках максимального подъема. (0,33; 1; 3).

33. Точка движется по окружности радиусом 20 см с постоянным тангенциальным ускорением 5 см/с². Через сколько времени после начала движения нормальное ускорение точки будет вдвое больше тангенциального? (2,8 с).

34. Якорь электромотора вращался с частотой 50 с^-1. После выключения тока он стал двигаться равнозамедленно и, сделав 1680 оборотов, остановился. Определить угловое ускорение якоря. (-4,7 рад/с² ).

35. Нормальное ускорение точки, движущейся по окружности радиусом 1 м, задается уравнением

а_п = А + Вt²

(А = 2 м/с², В = 4 м/с⁴). Определить полное ускорение точки через 1 секунду после начала движения. (6,21 м/с²).

36. Тело движется по окружности радиусом 3 м. Зависимость пройденного телом пути от времени задается уравнением

S = Аt² + Вt

(А = 0,4 м/с², В = 0,1 м/с). Определить нормальное, тангенциальное и полное ускорения тела через 1 секунду после начала движения. (0,27 м/с², 0,8 м/с², 0,84 м/с²).

37. Материальная точка начинает двигаться по окружности радиусом 12,5 м с постоянным тангенциальным ускорением 0,5 м/с². Определить угол, который образует вектор полного ускорения с вектором скорости через 5 секунд после начала движения. (45°).

38. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением j = Аt² (А = 0,1 рад/с²). Определить полное ускорение точки на ободе диска к концу второй секунды после начала движения, если линейная скорость точки в этот момент времени равна 0,4 м/с. (0,26 м/с²).

39. Зависимость угла поворота радиуса диска от времени при его вращении задается уравнением

j = А + Вt³

(А = 2 рад, В = 4 рад/с³). Определить угол поворота j, при котором вектор полного ускорения точек на ободе диска составляет с радиусом диска угол 45°. (2,67 рад).

40. Колесо радиусом 10 см вращается вокруг неподвижной оси, проходящей через его центр так, что зависимость линейной скорости точек на ободе колеса от времени задается уравнением

V = Аt + Вt²,

где А = 3 см/с, В = 1 см/с³. Какой угол составляет вектор полного ускорения с радиусом колеса через 5 секунд после начала движения? (4° 38^¢).

41. Колесо радиусом 6,1 см вращается с постоянным угловым ускорением. Через 0,5 с после начала движения полное ускорение колеса стало равно 13,6 см/с². Определить угловое ускорение колеса. (2 рад/с²).

42. Точка движется по окружности радиусом 15 см с постоянным тангенциальным ускорением. К концу четвертого оборота после начала движения линейная скорость точки составляет 15 см/с. В какой момент времени после начала движения нормальное ускорение точки будет равно 1,5 см/с²? (16 с).

43. По окружности радиусом 10 м вращается материальная точка. В некоторый момент времени ее нормальное ускорение равно 4,9 м/с², а вектор полного ускорения образует с вектором нормального ускорения угол 60°. Найти скорость, тангенциальное и полное ускорения точки в этот момент времени. (7 м/с, 8,5 м/с², 9,8 м/с²).

44. Диск радиусом 5 см вращается вокруг неподвижной оси, проходящей через его центр так, что зависимость угловой скорости от времени задается уравнением

w = 2Аt + 5Вt⁴

(А = 2 рад/с², В = 1 рад/с⁵). Определить полное ускорение точек, лежащих на ободе диска, к концу первой секунды после начала движения и число оборотов, сделанных диском за первую секунду. (4,22 м/с², 0,477).

45. Диск радиусом 10 см вращается вокруг неподвижной оси, проходящей через его центр, так, что тангенциальное ускорение точек на ободе диска зависит от времени по закону а_t = 2t (м/с²). Определить нормальное ускорение этих точек в момент времени, когда диск сделает один полный оборот после начала движения. (24,7 м/с).

46. Материальная точка движется в плоскости XY. Зависимости координат X и Y от времени имеет вид

Х = 2 + 4t² - 3t³, Y = 3t - 2t²,

где X и Y измеряются в метрах, время t в секундах. Найти величину и направление скорости и ускорения материальной точки в моменты времени t₁ = 0 и t₂ = 1 c. (V₁ = 3 м/с, V₂= 1,4 м/с, а₁ = 9 м/с², а₂= 10,7 м/с²).

47. На цилиндр радиусом 4 см, который может вращаться вокруг неподвижной горизонтальной оси, совпадающей с осью цилиндра, намотана нить. К концу нити привязали груз и предоставили ему опускаться. Двигаясь равноускоренно, груз за 3 секунды опустился на 1,5 м. Определить угловое ускорение цилиндра и число оборотов, сделанных им за это время. (8,3 рад/с², 6).

48. Колесо радиусом 10 см вращается вокруг неподвижной оси, проходящей через его центр, так, что угловое ускорение зависит от времени по закону e = 3t (рад/с²). Определить полное ускорение точек на ободе колеса и число оборотов, сделанных колесом к моменту времени t = 2 с после начала движения. (3,65 м/с², 0,64)

49. Точка начинает двигаться по окружности с постоянным тангенциальным ускорением. Через 0,5 с после начала движения угол между полным и нормальным ускорениями стал равен 45°. Определить угловое ускорение точки и количество оборотов, сделанных точкой к этому моменту времени. (4 рад/с², 0,08).

50. Точка начинает двигаться по некоторой траектории так, что ее нормальное и тангенциальное ускорения зависят от времени по законам: а_t =2t² (м/с²), а_n = 2t² (м/с²).

Определить радиус кривизны траектории движения материальной точки через одну секунду после начала движения. (0,22 м)

51. Материальная точка движется в плоскости XY так, что законы ее движения вдоль осей X и Y заданы уравнениями:

X = 2t - t³ (м), Y = t² + 2t³ (м).

Определить радиус кривизны траектории точки через 1 с после начала движения. (15,4 м).

52. Материальная точка движется в плоскости XY так, что законы ее движения вдоль осей X и Y заданы уравнениями:

X = -6 + 0,1t³ (м), Y = 0,2t³ - t² (м).

Определить нормальное, тангенциальное и полное ускорения точки через 2 секунды после начала движения. (1,2 м/с², 0,4м/с², 1,26 м/с²).

53. Твердое тело вращается вокруг неподвижной оси по закону

j = Аt - Вt³,

где А = 6 рад/с и В=2 рад/с³ .Найти: 1) средние значения угловой скорости и углового ускорения за промежуток времени от начала движения до остановки; 2) угловое ускорение в момент остановки. (4 рад/с, -6 рад/с², -12 рад/с²).

54. Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением e = Вt (В = 0,02 рад/с²). Через сколько времени после начала движения вектор полного ускорения произвольной точки тела будет составлять угол 60° с вектором ее линейной скорости? (7 c).

55. Найти радиус вращающегося колеса, если известно, что линейная скорость точки, лежащей на ободе, в 2,5 раза больше линейной скорости точки, лежащей на 5 см ближе к оси колеса. (8,3 см).

56. С какой скоростью двигалась повозка при киносъемке, если при демонстрации кинофильма на экране колеса, имеющие по 19 спиц, кажутся не вращающимися? Диаметр колес 0,58 м, киносъемка производилась со скоростью 17 кадров в секунду. (1,63 м/с).

57. Колесо автомашины вращается равнозамедленно. За 2 минуты колесо изменило частоту вращения от 240 до 60 мин^-1. Определить угловое ускорение колеса и число полных оборотов, сделанным им за это время. (-0,157 рад/с², 300).

58. Радиус-вектор материальной точки изменяется со временем по закону ,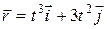

где 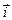и 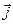-орты осей х и y. Определить для момента времени t = 1 с модули скорости и ускорения. (6,7 м/с; 8,48 м/с²).

59. Точка движется по окружности радиусом 20 см с постоянным тангенциальным ускорением 5 см/с². Через какое время после начала движения нормальное ускорение точки будет а) равно тангенциальному; б) вдвое больше тангенциального? (2 с, 2,8 с).

ДИНАМИКА

I. Динамика материальной точки и тела, движущегося поступательно.

1. Второй закон Ньютона

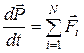
где 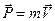- импульс тела, 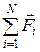-геометрическая сумма сил, действующих на тело массой m, N - число действующих сил.

Если масса тела постоянна, то

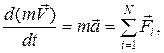
где 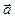- ускорение, приобретаемое телом под действием сил.

2. Третий закон Ньютона

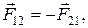
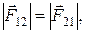
где 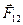и 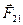- силы, с которыми взаимодействуют тела.

3. Сила упругости

,

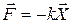где k - коэффициент упругости (жесткости), Х - абсолютная деформация.

4. Сила гравитационного взаимодействия

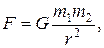
где G - гравитационная постоянная, m₁ и m₂ - массы взаимодействующих материальных точек, r - расстояние между их центрами масс.

5. Сила трения скольжения

,

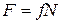где 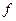- коэффициент трения, N - сила нормального давления. Сила трения скольжения направлена против движения.

II. Динамика вращательного движения.

1. Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси

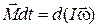
где 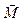- момент силы, действующий на тело в течение времени dt, I - момент инерции тела относительно оси вращения, w - угловая скорость вращения. В случае постоянного момента инерции

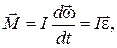
где e - угловое ускорение.

2. Момент силы, действующей на тело, относительно некоторой точки О

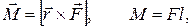
где l - плечо силы F, 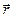- радиус-вектор точки приложения силы, проведенный из точки О.

3. Момент инерции материальной точки массой m

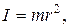
где r - расстояние материальной точки до оси вращения.

Момент инерции твердого тела

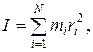
где r_i - расстояние материальной точки массой m_i до оси вращения.

В случае непрерывного распределения масс

.

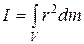4. Теорема Штейнера

Момент инерции тела I относительно произвольной оси

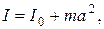
где I₀ - момент инерции тела относительно оси, проходящей через центр масс параллельно заданной оси, 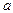- расстояние между осями.

5. Моменты инерции некоторых тел правильной геометрической формы:

Тело	Ось, относительно которой находится момент инерции	Формула момента инерции
Однородный тонкий стержень массой m и длиной l	Проходит через центр тяжести стержня пер-пендикулярно ему	(1/12) ml2
То же	Проходит через конец стержня перпендику-лярно ему	(1/3) ml2
Однородный шар массой m и радиусом R	Проходит через центр шара	(2/5) mR2
Сплошной однородный цилиндр или диск массой m и радиусом R	Проходит через центр диска перпендикулярно ему	(1/2) mR2
Тонкое кольцо, обруч, труба массой m и радиусом R	Проходит через центр перпендикулярно плос-кости тела (основания).	mR2