Сравнительный анализ прямолинейно-параллельного и плоскорадиального фильтрационных потоков идеального газа
Дифференциальные уравнения фильтрации газа
По линейному закону
Уравнение неразрывности потока сжимаемой жидкости в деформируемой пористой среде имеет вид:
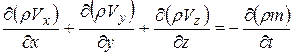 . (7.1)
. (7.1)
Уравнения движения в горизонтальном фильтрационном потоке записываются в виде:
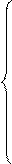 |
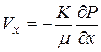 ,
,
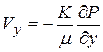 ,
,
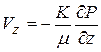 . (7.2)
. (7.2)
Введем функцию P следующим образом. Примем, что ее дифференциал равен:
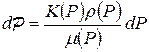 ,
,
тогда
 |
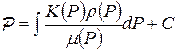 - функция Л.С.Лейбензона. (7.3)
- функция Л.С.Лейбензона. (7.3)
От дифференциала функции Л.С.Лейбензона, перейдем к частным производным:
 |
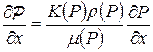 ;
;
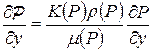 ;
;
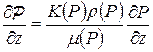 . (7.4)
. (7.4)
Запишем уравнения движения для массовых скоростей фильтрации с учетом соотношений (7.4):
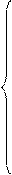 |
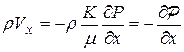 ;
;
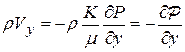 ;
;
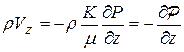 .
.
Тогда уравнение неразрывности (7.1) можно записать в виде:
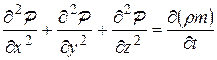 (7.6)
(7.6)
или
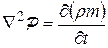 . (7.6’)
. (7.6’)
В случае установившейся фильтрации правая часть уравнений (7.6) обращается в 0, в результате чего можно записать:
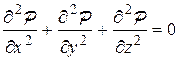 (7.7)
(7.7)
или 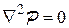 .
.
Следовательно, функция Л.С.Лейбензона удовлетворяет уравнению Лапласа.
Аналогия между фильтрацией жидкости и идеального газа
Введение функции Л.С.Лейбензона в дифференциальные уравнения теории фильтрации позволяет установить аналогию между установившейся фильтрацией сжимаемого флюида (газа) и установившейся фильтрацией несжимаемой жидкости.
В наиболее простом случае можно считать K=const. При малых пластовых давлениях и небольших депрессиях можно также пренебречь зависимостью вязкости m от давления. Такое допущение справедливо для идеальных сред, в которых отсутствует внутреннее трение, обусловленное процессами внутреннего молекулярного обмена.
Тогда функцию Л.С.Лейбензона можно представить в виде:
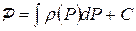 ,
,
при этом 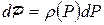 .
.
Сравним две записи закона Дарси в дифференциальной форме – для установившейся фильтрации несжимаемой жидкости и для установившейся фильтрации газа.
| Жидкость | Газ |
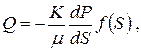 где Q=const – объемный расход жидкости; f(S) – площадь поперечного сечения струи где Q=const – объемный расход жидкости; f(S) – площадь поперечного сечения струи | 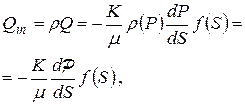 где Qm=rQ=const – массовый расход газа где Qm=rQ=const – массовый расход газа |
Данные уравнения однотипны, следовательно, все формулы, полученные для установившейся фильтрации жидкости, можно применять и для установившейся фильрации газа, используя аналогию следующих показателей:
| Несжимаемая жидкость | Газ | |
| объемный расход Q | - | массовый расход Qm |
| давление Р | - | функция Л.С.Лейбензона P |
| объемная скорость фильтрации V | - | массовая скорость фильтра-ции rV |
Сравнительный анализ прямолинейно-параллельного и плоскорадиального фильтрационных потоков идеального газа
Исследованиями Б.Б.Лапука было установлено, что фильтрацию газа в реальных пластах можно рассматривать как изотермический процесс, для которого справедлив закон Бойля-Мариотта. При T=const
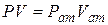
или
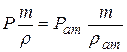 ,
,
где m – масса газа.
Отсюда

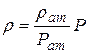 - уравнение состояния идеального газа.
- уравнение состояния идеального газа.
С учетом уравнения состояния идеального газа выражение функции Л.С.Лейбензона приобретает вид:
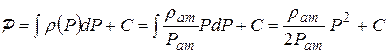 .
.
| Характерис-тика | Прямолинейно-параллельный поток | Плоскорадиальный поток |
| Распределение давления | 1. 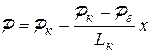 2. 2. 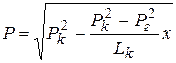 | 1. 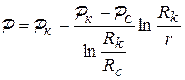 2. 2. 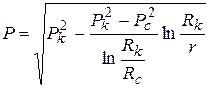 |
| Градиент давле-ния | 1. 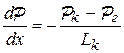 2. 2. 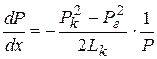 | 1. 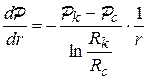 2. 2. 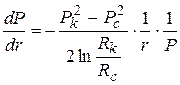 |
| Скорость фильтрации | 1. 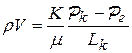 2. 2. 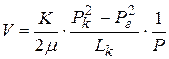 | 1. 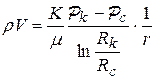 2. 2. 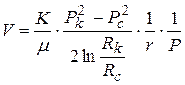 |
| Дебит газа, при-веденнй к атмо-сферному дав-лению | 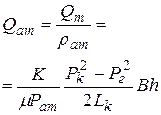 | 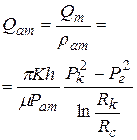 |
| Средневзвешен-ное пластовое давление | 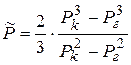 | 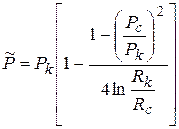 |
Анализируя соотншения, можно отметить следующее.
В прямолинейно-параллельном потоке:
а) давление по длине пласта изменяется по параболическому закону, зависимость Р2(x) - линейная;
б) объемный расход газа, приведенный к атмосферному давлению, постоянный по длине пласта;
в) скорость фильтрации и градиент давления возрастают при приближении к галерее. Физически возрастание скорости фильтрации вдоль газового потока происходит за счет расширения газа при снижении давления.
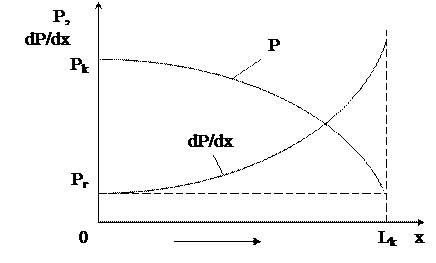 |
В плоскорадиальном потоке:
а) распределение давления подчинено логарифмическому и параболическому законам, поэтому в газовом потоке, в отличие от потока жидкости, имеет место резкое падение давления вблизи скважины и весьма малое – вдали от нее. Площадь и объем пласта с пониженным давлением вблизи скважины значительно меньше объема газового пласта в целом. Поэтому в газонасыщенном пласте давление повсюду считается одинаковым, приблизительно равным давлению на контуре питания;
б) градиент давления и скорость фильтрации вблизи забоя газовой скважины резко возрастают как за счет уменьшения r, так и за счет падения давления Р.
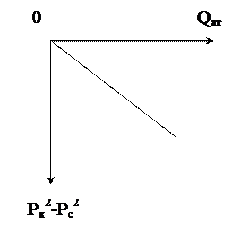
Индикаторная диаграмма при фильтрации газа строится в координатах 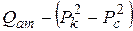 и в установившемся плоскорадиальном потоке имеет прямолинейный характер.
и в установившемся плоскорадиальном потоке имеет прямолинейный характер.
