Глава 1. элементы линейной алгебры
§ 1. МАТРИЦЫ И АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ С НИМИ.
Определение. Матрицей называется прямоугольная табли –ца состоящая из 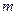 строк и
строк и 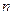 столбцов, заполненная либо числами, либо некоторыми символами, при этом говорят, что она имеет размерность
столбцов, заполненная либо числами, либо некоторыми символами, при этом говорят, что она имеет размерность 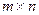 . Общий вид матрицы можем представить следующим образом:
. Общий вид матрицы можем представить следующим образом:

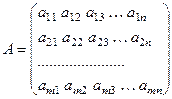 ,
, 
или, в более компактном виде: 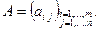
Если 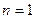 , т.е. матрица размерности
, т.е. матрица размерности 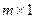 , то матрицу на- зывают вектор – столбцом, если
, то матрицу на- зывают вектор – столбцом, если 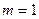 , т.е. матрица размер -ности
, т.е. матрица размер -ности 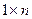 , то её называют вектор – строкой. Матрица, у ко- торой все элементы равны нулю, называется нулевой. Матри -ца, у которой число строк
, то её называют вектор – строкой. Матрица, у ко- торой все элементы равны нулю, называется нулевой. Матри -ца, у которой число строк 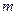 равно числу столбцов
равно числу столбцов 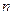 назы – ется квадратной матрицей порядка
назы – ется квадратной матрицей порядка 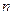 .
.
Элементы 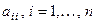 образуют главную диагональ квад- ратной матрицы. Если равны нулю все элементы квадратной матрицы, кроме элементов главной диагонали, которые не все равны нулю, то матрица называется диагональной порядка
образуют главную диагональ квад- ратной матрицы. Если равны нулю все элементы квадратной матрицы, кроме элементов главной диагонали, которые не все равны нулю, то матрица называется диагональной порядка 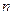 . Если все элементы главной диагонали диагональной матрицы равны между собой, то она называется скалярной. Диагональ- ная матрица, все диагональные элементы которой равны 1, называпется единичной. Если все элементы квадратной матри- цы, расположенные выше (или ниже) главной диагонали равны нулю, то матрица называется треугольной. Приведём приме -ры перечисленных матриц:
. Если все элементы главной диагонали диагональной матрицы равны между собой, то она называется скалярной. Диагональ- ная матрица, все диагональные элементы которой равны 1, называпется единичной. Если все элементы квадратной матри- цы, расположенные выше (или ниже) главной диагонали равны нулю, то матрица называется треугольной. Приведём приме -ры перечисленных матриц:
1. Вектор – столбец размерности 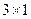 :
:
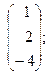
2. Вектор – строка размерности 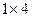 :
: 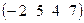 :
:
3. Нулевая матрица размерности 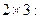
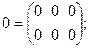
4 Квадратная матрица порядка 3:
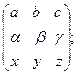
5. Диагональная матрица четвёртого порядка:
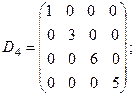
6. Скалярная матрица второго порядка :
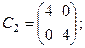
7. Единичная матрица третьего порядка:
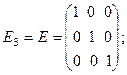
8. Треугольные матрицы:
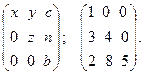
Две матрицы 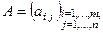 и
и 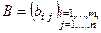 называют- ся равными, если они имеют одинаковые размерности
называют- ся равными, если они имеют одинаковые размерности 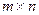 и совпадают элементы с одинаковыми индексами (т.е. совпа- дают элементы, расположенные на одинаковых местах):
и совпадают элементы с одинаковыми индексами (т.е. совпа- дают элементы, расположенные на одинаковых местах):
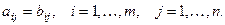
В этом случае пишут 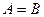 .
.
АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ С МАТРИЦАМИ
1. Умножение матрицы на число.: возможно для матриц лю-
бой размерности. При умножении матрицы на число каждый элемент матрицы умножается на это число, т.е.
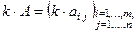 ,
,
Например, если 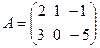 , то
, то 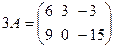 .
.
2. Алгебраическое сложение матриц (т.е. сложение и вычи- тание) можно выполнять только для матриц одинаковой раз –мерности и производится поэлементно, т.е., если даны две матрицы 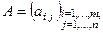 и
и 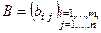 , то
, то
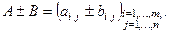
Например, если 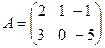 ,
, 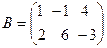 , то
, то
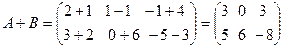 ;
;
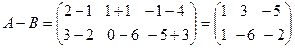 .
.
3. Умножение матриц возможно только в том случае, ес- ли число столбцов первой матрицы равно числу строк вто- рой матрицы. В результате умножения получается матрица, у которой число строк равно числу строк первой матрицы, а число столбцов равно числу столбцов второй матрицы.
Замечание. Согласно этому правилу, умножение матриц возможно далеко не всегда. Кроме того, даже если умножение матриц возможно, нельзя менять их местами при умножении, так как это может привести к совершенно различным резуль- татам.
Таким образом, если 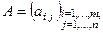 , а
, а 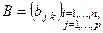 , т.е. в матрице
, т.е. в матрице 
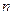 столбцов, а в матрице
столбцов, а в матрице 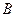
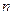 строк, то после умножения получится матрица
строк, то после умножения получится матрица 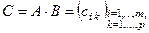 , где элемент
, где элемент 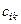 равен сумме произведений соответствующих элементов
равен сумме произведений соответствующих элементов 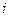 -й строки матрицы
-й строки матрицы  и
и 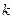 -го столбца матрицы
-го столбца матрицы 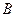 , т.е.
, т.е.
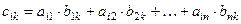 ,
,
где 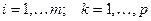 .
.
Чтобы понятнее был способ умножения матриц, рассмотрим следующий пример 1:
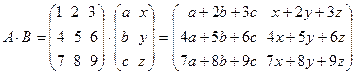 .
.
Ещё один пример 2 умножения числовых матриц:
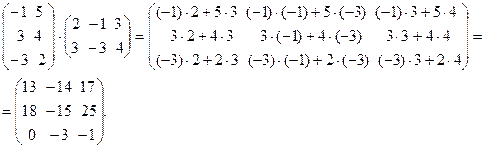
Перемножим эти же матрицы в другом порядке:
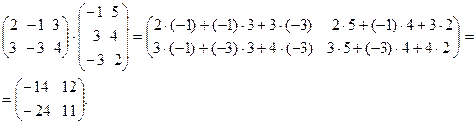 Умножение этих матриц также было возможно, но в резуль- тате умножения получили совершенно другую матрицу, более того, даже матрицу другой размерности.
Умножение этих матриц также было возможно, но в резуль- тате умножения получили совершенно другую матрицу, более того, даже матрицу другой размерности.
Матрицы же, рассмотренные в примере 1, вообще нельзя перемножить в другом порядке, так как у второй матрицы 2 столбца, а у первой матрицы 3 строки и, согласно правилу умножения, умножение таких матриц невозможно. Поэтому ум- ножение матриц антикоммутативно, т.е., в общем случае, 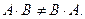
Деление для матриц не определяется, но можно для неко- торых матриц ввести понятие обратной матрицы (только для квадратных невырожденных матриц).
Определение. Матрица 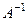 называется обратной к матри- це
называется обратной к матри- це  , если выполняется равенство:
, если выполняется равенство:
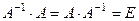 ,
,
где 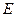 - единичная матрица.
- единичная матрица.
В завершение параграфа отметим следующие свойства алгебраических действий с матрицами.
Пусть 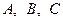 - некоторые матрицы,
- некоторые матрицы, 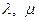 - числа. Тогда можно легко убедиться в справедливости следующих равенств:
- числа. Тогда можно легко убедиться в справедливости следующих равенств:
1) 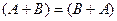 (коммутативность сложения);
(коммутативность сложения);
2) 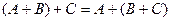 (ассоциативность сложения);
(ассоциативность сложения);
3) Для любой матрицы  размерности
размерности 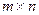 существует нулевая матрица
существует нулевая матрица 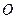 той же размерности, такая что выполнено:
той же размерности, такая что выполнено:
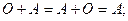
4) Для любой матрицы  существует противоположная мат- рица
существует противоположная мат- рица 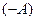 , такая что
, такая что 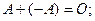
5) 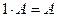 для любой матрицы
для любой матрицы 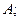
6) 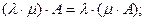
7) 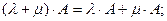
8) 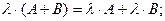
9) 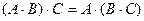 , если умножение возможно (ассо -циативность умножения);
, если умножение возможно (ассо -циативность умножения);
10) 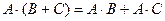 , если все эти операции воз -можны (дистрибутивность умножения);
, если все эти операции воз -можны (дистрибутивность умножения);
11) 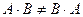 (антикоммутативность);
(антикоммутативность);
12) Для любой невырожденной квадратной матрицы су -ществует обратная матрица, такая что 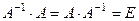 .
.
§ 2 ОПРЕДЕЛИТЕЛИ МАТРИЦ И ИХ СВОЙСТВА
Любой квадратной матрице  по некоторому правилу можно поставить в соответствие некоторое число, которое называется её определителем и обозначается либо
по некоторому правилу можно поставить в соответствие некоторое число, которое называется её определителем и обозначается либо 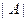 , ли- бо
, ли- бо 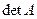 , либо просто
, либо просто 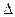 .
.
Для матрицы второго порядка
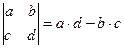 .
.
Например:
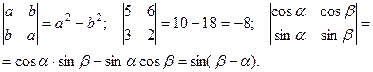
Для вычисления определителей третьего порядка удобно воспользоваться, так называемым правилом треугольников:
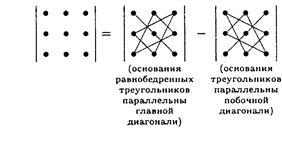
Согласно этому правилу, определитель матрицы третьего порядка вычисляется по формуле:
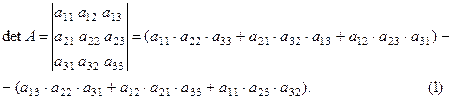
Замечание 1. Следует заметить, что в данном выражении каждое произведение содержит элемент каждой строки и каж -дого столбца исходной матрицы, что позволяет доказывать не- которые свойства определителя.
Пример: 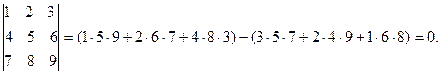
Замечание 2. Для вычисления определителей более высо -кого порядка нет таких простых формул, но так же, как и оп -ределитель третьего порядка, определитель произвольного по -рядка 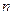 является суммой
является суммой 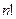 слагаемых, в которые входят по одному элементу из каждой строки и каждого столбца мат- рицы с определённым знаком. Вычисление определителей по- рядка, большего чем 3, производится с помощью понижения порядка, методами, которые будут рассмотрены ниже.
слагаемых, в которые входят по одному элементу из каждой строки и каждого столбца мат- рицы с определённым знаком. Вычисление определителей по- рядка, большего чем 3, производится с помощью понижения порядка, методами, которые будут рассмотрены ниже.
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
1. Определитель транспонированной матрицы равен определителю исходной матрицы, т.е. 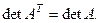 Это означает, что все свойства, относящиеся к строкам исходной матрицы, имеют место также и для столбцов матрицы. В са- мом деле, для случая матрицы третьего порядка,
Это означает, что все свойства, относящиеся к строкам исходной матрицы, имеют место также и для столбцов матрицы. В са- мом деле, для случая матрицы третьего порядка,
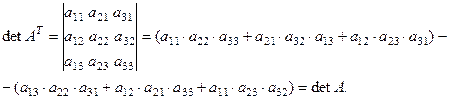
2. Знак определителя сменится на противоположный, если поменять местами две строки или два столбца матрицы.
Например:
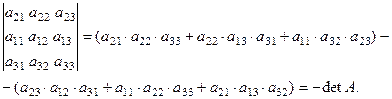
Если сравнить полученное выражение с формулой (1), то видим, что все произведения поменяли знак.
3. Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
В самом деле, если мы поменяем местами две одинаковые строки, то, по свойству 2, знак определителя должен сменить- ся на противоположный, хотя на самом деле, его значение не должно измениться, т.е. 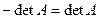 . Но это возможно только в случае
. Но это возможно только в случае 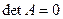 .
.
4. Умножение всех элементов одной строки (столбца) матрицы на некоторое число 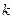 приводит к увеличению значения определителя в
приводит к увеличению значения определителя в 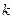 раз, например,
раз, например,
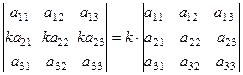 .
.
В самом деле, по замечанию 1, в каждом слагаемом в формуле (1) для вычисления определителя 3-го порядка, в произведениях содержится элемент каждой строки и каждого столбца матрицы, т.е. можно вынести общий множитель за скобку и получить в скобке значение первоначального опреде -лителя. То же самое, согласно замечанию 2, имеет место и для определителя произвольного порядка.
Следующее свойство также автоматически следуют из замечаний 1 и 2.
5. Если все элементы некоторой строки (столбца) матрицы равны нулю, то её определитель равен нулю.
6. Если две строки (столбца) матрицы пропорцио -нальны, то её определитель равен нулю.
(Это следствие свойств 3 и 4).
7. Если каждый элемент некоторой строки (столбца) матрицы равен сумме двух слагаемых, то определитель можно представить в виде суммы двух определителей, в первом из которых на месте данной строки (столбца) размещены первые, а во втором - вторые слагаемые.
Например:
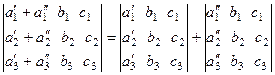 .
.
Это свойство легко проверить непосредственным вычисле- нием определителей.
8. Значение определителя не изменится, если к эле -ментам некоторой строки (столбца) матрицы добавить элементы другой строки (столбца), умноженные на одно и то же число.
Например, если
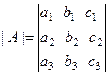 ,
, 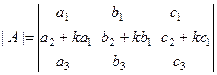 , то, по предыдущему свойству и свойству 6 ,
, то, по предыдущему свойству и свойству 6 ,
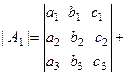
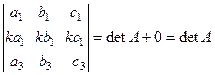 .
.
Для определителей порядка 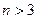 доказательство всех перечисленных свойств аналогично.
доказательство всех перечисленных свойств аналогично.
Чтобы сформулировать следующие свойства определителя, необходимо ввести два определения.
Определение 1 Минором 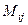 элемента
элемента 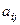 квадратной мат- рицы
квадратной мат- рицы
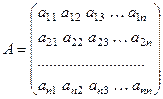
называется определитель матрицы, которая получается из мат- рицы  после вычёркивания
после вычёркивания 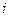 - й строки и
- й строки и 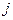 - го столбца, т.е.
- го столбца, т.е.
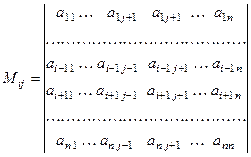 .
.
Определение 2. Алгебраическим дополнением 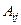 элемен- та
элемен- та 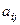 квадратной матрицы
квадратной матрицы  называется минор этого эле- мента с соответствующим знаком, т.е.
называется минор этого эле- мента с соответствующим знаком, т.е.
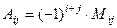 .
.
9. Определитель равен сумме произведений элемен -тов некоторой строки или столбца на их алгебраичес- кие дополнения, т.е.
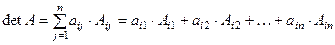 ,
,
или
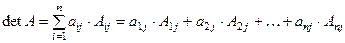
где 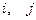 любое из чисел
любое из чисел 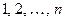 . Эта формула называется разложением определителя по элементам
. Эта формула называется разложением определителя по элементам 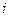 - й строки, или разложением по элементам
- й строки, или разложением по элементам 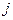 -го столбца, соответственно, ( или разложением Лапласа.).
-го столбца, соответственно, ( или разложением Лапласа.).
Доказывать это свойство не будем, однако его достаточно легко проверить на примерах при вычислении определителей.
10. Сумма произведений элементов некоторой вектор – строки 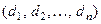 и алгебраических дополнений эле- ментов
и алгебраических дополнений эле- ментов 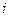 - й матрицы
- й матрицы  численно равна значению опре- делителя матрицы, которая получается из матрицы
численно равна значению опре- делителя матрицы, которая получается из матрицы  заменой
заменой 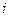 - й строки этим вектором, например
- й строки этим вектором, например
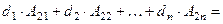
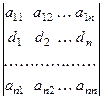 .
.
Аналогичное свойство имеет место и для столбцов .
11. Сумма произведений элементов некоторой строки (столбца) на алгебраические дополнения элементов дру -гой строки (столбца) равна нулю.
Это следует из предыдущего свойства и свойства 3 (опре -делитель с одинаковыми строками или столбцами равен нулю).
12. Определитель треугольной матрицы равен произ- ведению элементов главной диагонали.
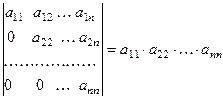 .
.
Это свойство также легко проверяется непосредственно, вы- числением определителя.
Рассмотрим пример вычисления определителя 4 – го поряд- ка двумя способами: 1) понижением порядка с помощью разло- жения по элементам строки (разложением Лапласа) и 2) пони- жением порядка с помощью элементарных преобразований (т.е., используя основные свойства определителей).
Пример. Вычислить определитель:
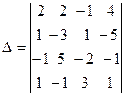 .
.
Первый способ: разложим определитель по элементам 1 – й строки
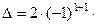
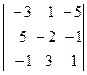 +
+ 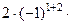
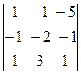 +
+
+ 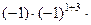
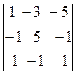 +4
+4 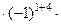
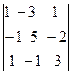 =
=
= 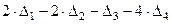 .
.
Вычислим каждый из полученных определителей третьего порядка по отдельности также используя разложение по эле- ментам первой строки, хотя можно было бы воспользоваться и «правилом треугольников».
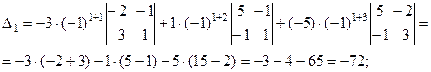
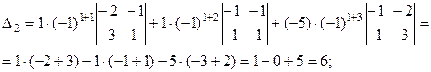
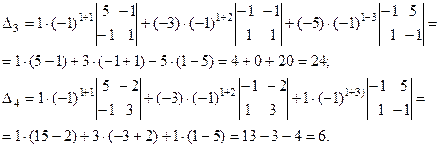
Тогда 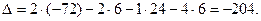
Второй способ: вычислим тот же определитель с помощью элементарных преобразований.
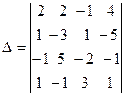 =
=
Получим нули в первом столбце, для чего умножим третью строку на ( 2 ) и прибавим к первой строке и ту же третью строку прибавим к второй и четвёртой строке. По свойству 8, значение определителя при этом не изменится. После получе-ния нулей в первом столбце, разложив полученный определи -тель по элементам первого столбца, получим
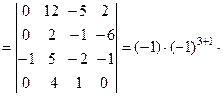
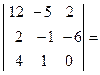
получим ноль в последней строке, умножив второй столбец на ( - 4 ) и прибавив его к первому столбцу
= - 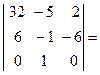
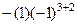
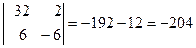 .
.
Как видим, вычисление определителя вторым способом бо -лее экономично, т.е. быстрее приводит к результату. Кроме то- го, вычисление определителей порядка большего чем 4 пер -вым способом приведёт к очень громоздким вычислениям, по- этому при вычислении определителей высокого порядка целе- сообразно пользоваться вторым способом.
§ 3 ОБРАТНАЯ МАТРИЦА
В § 1 было введено понятие обратной матрицы, как матри- цы, удовлетворяющей условию 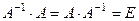 . Теперь же, зная свойства определителей, можем доказать теорему о виде обратной матрицы, при условии, что она невырожденная т.е. её определитель
. Теперь же, зная свойства определителей, можем доказать теорему о виде обратной матрицы, при условии, что она невырожденная т.е. её определитель 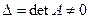 .
.
ТЕОРЕМА. Для любой невырожденной квадратной матрицы обратную матрицу можно найти по формуле:
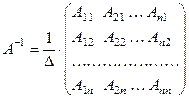 ,
,
где 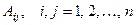 - алгебраические дополнения соот- ветствующих элементов матрицы
- алгебраические дополнения соот- ветствующих элементов матрицы  , причём алгебраические дополнения элементов строк матрицы
, причём алгебраические дополнения элементов строк матрицы  записаны столбцами в матрице
записаны столбцами в матрице 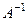 .
.
Проверим, что данная матрица в самом деле является обратной к матрице  , использовав определение обратной матрицы. В самом деле,
, использовав определение обратной матрицы. В самом деле,
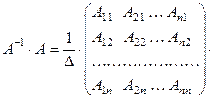
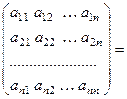
Используя правило умножения матриц, а также свойства 9 и 11 определителей, получим:
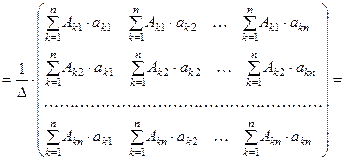
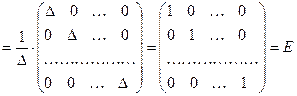 .
.
При умножении матриц в обратном порядке также получим единичную матрицу (можно проверить непосредственно), т.е. матрица 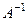 в самом деле является обратной к матрице
в самом деле является обратной к матрице  .
.
Пример. Найти матрицу, обратную к матрице 
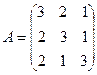 .
.
Сначала найдём её определитель:
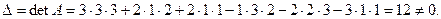 Следовательно матрица невырожденная и для неё можно найти обратную матрицу. Для этого найдём алгебраические дополнения всех элементов матрицы.
Следовательно матрица невырожденная и для неё можно найти обратную матрицу. Для этого найдём алгебраические дополнения всех элементов матрицы.
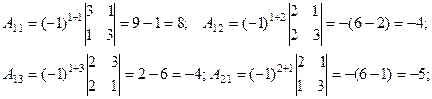
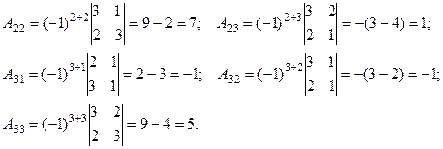
Тогда
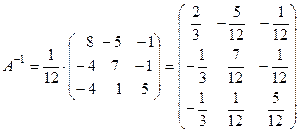 .
.
Сделаем проверку
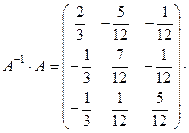
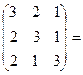
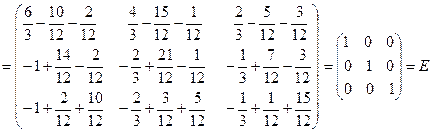 Т.о., в самом деле, получили обратную матрицу.
Т.о., в самом деле, получили обратную матрицу.
Отдельно рассмотрим случай нахождения обратной матрицы второго порядка. Пусть дана матрица
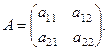
Тогда для данной матрицы
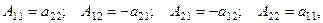
и обратная матрица имеет вид:
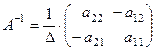 , т.е. элементы главной диагонали меняются местами, а эле -менты вспомогательной диагонали меняют знаки.
, т.е. элементы главной диагонали меняются местами, а эле -менты вспомогательной диагонали меняют знаки.
Пример. Решить матричное уравнение:
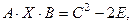 если
если 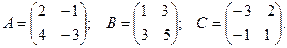
РЕШЕНИЕ: Из этого равенства имеем:
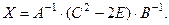
Для матрицы  :
: 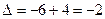 и
и 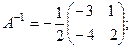 для матрицы
для матрицы 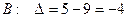 и
и 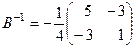 ;
;
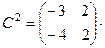
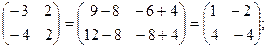
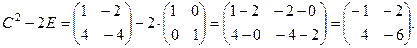
Тогда 
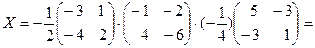
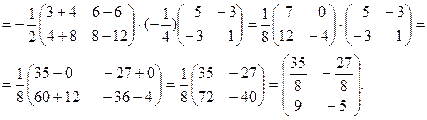
Приведём ещё одно определение, связанное с понятиями матрицы и определителя.
Рангом 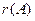 матрицы
матрицы  называется максимальный поря- док отличного от нуля минора данной матрицы. В этом опре- делении минором порядка
называется максимальный поря- док отличного от нуля минора данной матрицы. В этом опре- делении минором порядка 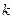 называется определитель, сос -тавленный из элементов матрицы
называется определитель, сос -тавленный из элементов матрицы  , расположенных на пере- сечении
, расположенных на пере- сечении 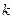 выбранных строк и
выбранных строк и 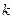 выбранных строк.
выбранных строк.
Например, найдём ранг матрицы
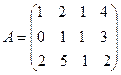 .
.
Миноры
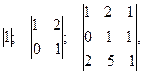
порядков 1, 2, 3, соответственно, расположенные в левом верхнем углу матрицы  , называются главными.
, называются главными.
Главный минор 2 – го порядка 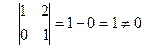 ,
,
Следовательно, 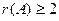 . Вычислим миноры третьего порядка:
. Вычислим миноры третьего порядка:
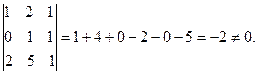
Поэтому 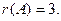
§ 4 СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Системой линейных алгебраических уравнений с 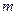 урав –нений с
урав –нений с 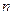 неизвестными называется система вида:
неизвестными называется система вида:
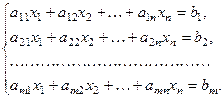 (1)
(1)
Уравнения данной системы являются линейными, так как все неизвестные величины 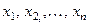 входят в уравнения толь- ко в первой степени, и алгебраическими, так как получены с применением конечного числа алгебраических операций сло- жения и умножения на число.
входят в уравнения толь- ко в первой степени, и алгебраическими, так как получены с применением конечного числа алгебраических операций сло- жения и умножения на число.
Решением системы (1) называется некоторый набор чисел 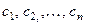 , при подстановке которых вместо неизвестных
, при подстановке которых вместо неизвестных 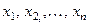 во все уравнения системы (1) получаем тож- дественные равенства.
во все уравнения системы (1) получаем тож- дественные равенства.
Это определение позволяет разделить системы вида (1) на два класса: системы, имеющие хотя бы одно решение, назы -ваются совместными, а системы, не имеющие ни одного ре -шения, называются несовместными. Совместные системы, име- ющие единственное решение, называются определёнными, а имеющие более одного решения (на самом деле, имеющие бесконечное число решений), называются неопределёнными.
Кроме того среди систем вида (1) выделяют так называ –емые однородные, т.е. системы, в которых все правые части равны нулю: 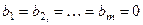 .
.
Рассмотрим теперь методы, позволяющие находить реше -ния системы (1), если они существуют.
Сначала рассмотрим системы, у которых число уравнений равно числу неизвестных, т.е. системы вида:
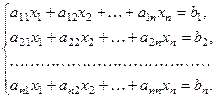 (2)
(2)
1. МАТРИЧНЫЙ СПОСОБ РЕШЕНИЯ СИСТЕМЫ.
Обозначим через:
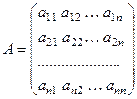 ,
, 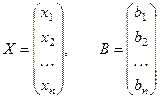
матрицу коэффициентов, столбец неизвестных и столбец пра -вых частей, соответственно. Тогда систему (2), учитывая пра -вила действия с матрицами, можем записать в более компакт- ной форме:
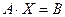 . (3)
. (3)
Если определитель матрицы  не равен нулю, т.е. матри -ца
не равен нулю, т.е. матри -ца  невырожденная, то данная матрица имеет обратную мат- рицу
невырожденная, то данная матрица имеет обратную мат- рицу 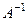 . Умножим обе части равенства (3) на
. Умножим обе части равенства (3) на 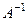 :
:
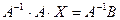 ,
,
а так как 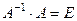 (по определению обратной матрицы), а
(по определению обратной матрицы), а 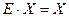 , то
, то
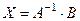 . (4)
. (4)
Эта формула даёт метод решения системы (2) средствами матричного исчисления, или просто матричный способ реше- ния системы (2).
Рассмотрим примеррешения системы матричным способом.
Пусть дана система линейных уравнений:
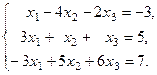
Для данной системы
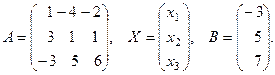
Найдём обратную матрицу 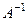 по известной формуле. Сначала найдём
по известной формуле. Сначала найдём
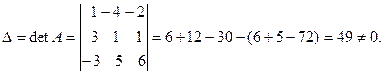
После этого вычислим алгебраические дополнения всех эле- ментов матрицы  .
.
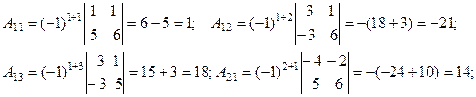
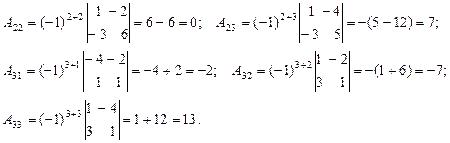
Следовательно,
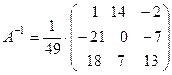 .
.
Тогда, по формуле (4), решение системы имеет вид:
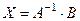
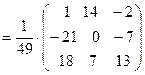
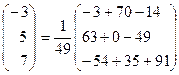 =
=
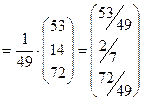 .
.
Таким образом 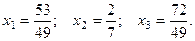 Сделаем про -верку, т.е. подставим полученное решение в систему:
Сделаем про -верку, т.е. подставим полученное решение в систему:
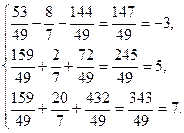
При подстановке получили тождественные равенства, следова- тельно, в самом деле получили решение системы.
2, ФОРМУЛЫ КРАМЕРА РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ
Ограничимся случаем системы трёх уравнений с тремя не -известными. В случае систем более высокого порядка пользо- ваться этими формулами очень трудоёмко.
Пусть дана система
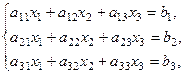
главный определитель которой
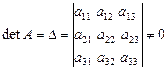 .
.
Умножим уравнения этой системы на соответствующие алгебраические дополнения элементов первого столбца основной матрицы данной системы, т.е.
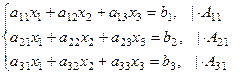
и сложим полученные уравнения. Получим
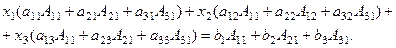
По свойству 9 определителей, первая скобка равна 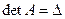 , по свойству 11, вторая и третья скобки равны нулю, а, по свойству 10, правая часть равна определителю матрицы, в ко– торой первый столбец заменён столбцом правых частей систе- мы, т.е.
, по свойству 11, вторая и третья скобки равны нулю, а, по свойству 10, правая часть равна определителю матрицы, в ко– торой первый столбец заменён столбцом правых частей систе- мы, т.е.
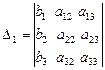 .
.
Получаем 
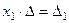 . Аналогично, умножая уравнения систе -мы на алгебраические дополнения второго и третьего столбца, соответственно, получим уравнения:
. Аналогично, умножая уравнения систе -мы на алгебраические дополнения второго и третьего столбца, соответственно, получим уравнения: 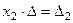 и
и 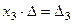 , где
, где 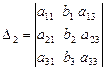 и
и 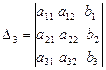 .
.
Отсюда получаются формулы Крамера :
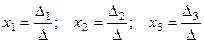 . (5)
. (5)
Таким образом, данный способ решения системы 3 – го сводится к вычислению четырёх определителей. В принципе этот метод можно применять и для произвольных систем с одинаковым числом уравнений и неизвестных с невырожден- ными матрицами коэффициентов, но вычисление определи -телей более высокого порядка, чем три, довольно громоздко.
Рассмотрим пример: решить систему по формулам Крамера.
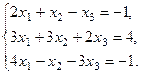
Главный определитель этой системы:
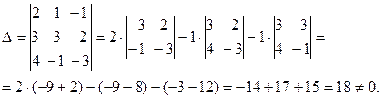
Найдём остальные определители:
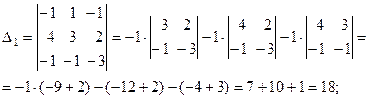
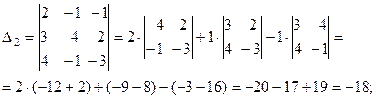
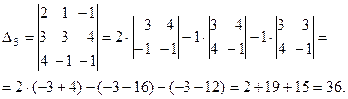
Тогда получаем решение: 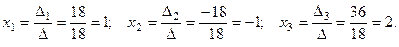
Подставив эти значения в уравнения системы вместо неиз -вестных, получим тождественные равенства.
И матричный способ решения систем, и формула Крамера позволяют решать системы, у которых число уравнений равно числу неизвестных с невырожденными матрицами коэффициен- тов. Следующий метод применим для произвольных систем.
3 МЕТОД ГАУССА (МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ
ИСКЛЮЧЕНИЙ)
Рассмотрим произвольную систему (1) линейных уравнений:
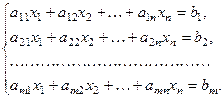
Две системы вида (1) называются эквивалентными, если любое решение одной из них является решение другой и нао- борот, или в случае, если обе системы несовместны.
Следующие преобразования систем, которые приводят к эквивалентным системам, называются элементарными, а иногда просто эквивалентными преобразованиями.
1. Можно поменять местами любые два уравнения сис –темы.
2. Можно умножить каждое слагаемое уравнения на одно и то же число, отличное от нуля.
3. Можно сложить любые два уравнения, а результат сложения записать вместо одного из уравнений.
Сущность метода Гаусса заключается в последовательном исключении неизвестных из уравнений системы. Сначала из первого уравнения выражаем 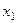 и подставляем во все ос –тальные уравнения. После этого из полученного второго уравнения выражаем
и подставляем во все ос –тальные уравнения. После этого из полученного второго уравнения выражаем 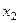 и подставляем во все следующие уравнения и так далее.
и подставляем во все следующие уравнения и так далее.
Все преобразования такого рода удобно выполнять, вос – пользовавшись так называемой расширенной матрицей сис – темы:

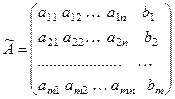 .
.
Матрица, расположенная слева от вертикальной черты, назы -вается основной, а вся матрица расширенной (здесь справа от черты стоят элементы правой части системы). Элементар- ные преобразования уравнений системы равносильны эквива - лентным преобразованиями строк расширенной матрицы сис –темы:
1. Можно поменять местами любые две строки матрицы 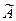 .
.
2. Любую строку матрицы 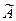 можно умножить на любое отличное от нуля число.
можно умножить на любое отличное от нуля число.
3. Любую сроку матрицы 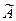 можно прибавить к любой другой строке.
можно прибавить к любой другой строке.
Чаще всего преобразования 2 и 3 заменяют следующим:
