Примеры решения задач. Пример. Однородная слабо проводящая среда с удельным сопротивлением r заполняет пространство между двумя коаксиальными цилиндрами радиуса а и b > a

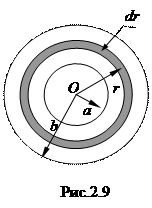
Пример. Однородная слабо проводящая среда с удельным сопротивлением r заполняет пространство между двумя коаксиальными цилиндрами радиуса а и b > a. Длина каждого цилиндра l. Найти сопротивление среды между цилиндрами.

Сопротивление среды между цилиндрами может быть рассчитано как непосредственно, так и с помощью закона Ома в дифференциальной форме.

Первый способ.

Рассчитаем сопротивление среды непосредственно. Выделим цилиндрический слой толщиной dr, как показано на рис. 2.9. Его сопротивлени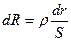е , где 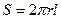- площадь боковой поверхности цилиндра радиуса r. Тогда 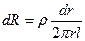. Выполняя интегрирование по r от a до b, получаем .

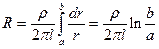Второй способ.

Пусть между цилиндрами поддерживается постоянная разность потенциалов U = j₁ - j₂. В проводящей среде при наличии поддерживаемой разности потенциалов между цилиндрами протекает ток плотности j, причем 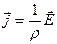. При этом сила тока есть величина постоянная и определяется потоком вектора плотности тока через боковую поверхность цилиндра S с произвольным радиусом основания а ≤ r ≤ b:

.

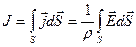Т.к. векторы 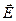и 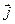перпендикулярны рассматриваемой боковой поверхности цилиндра в каждой точке (рис. 2.10), то потоки через основания равны нулю, т.е. 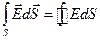. Учтем, что электрическая составляющая стационарного поля описывается законами электростатики, и воспользуемся теоремой Гаусса:

,

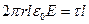где t - заряд единицы длины цилиндров (заряд, протекающий через проводящую среду, пополняется за счет работы источника тока). Таким образом, напряженность электрического поля в среде 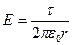. Тогда

.

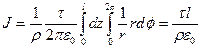С другой стороны,

.

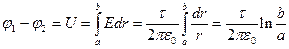Следовательно, 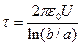и 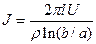. Отсюда, в соответствии с законом Ома, получаем .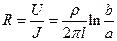