Метод lu-разложение матриц
Пусть 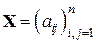 – данная
– данная 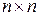 – матрица, а
– матрица, а 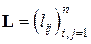 и
и 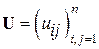 – соответственно нижняя (левая) и верхняя (правая) треугольные матрицы. Справедливо следующее утверждение.
– соответственно нижняя (левая) и верхняя (правая) треугольные матрицы. Справедливо следующее утверждение.
Теорема 5.1. Если все главные миноры квадратной матрицы 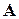 отличны от нуля, то существуют такие нижняя
отличны от нуля, то существуют такие нижняя 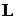 и верхняя
и верхняя 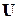 треугольные матрицы, что
треугольные матрицы, что 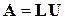 . Если элементы диагонали одной из матриц
. Если элементы диагонали одной из матриц 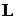 или
или 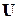 фиксированы (ненулевые), то такое разложение единственно.
фиксированы (ненулевые), то такое разложение единственно.
Определим 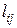 (при
(при 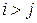 ) и
) и 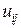 (при
(при 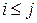 ) такие, чтобы
) такие, чтобы
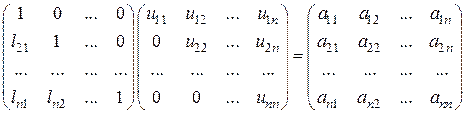
Выполнив перемножение матриц, на основе поэлементного приравнивания левых и правых частей приходим к 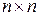 -матрице уравнений
-матрице уравнений
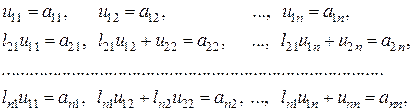
относительно 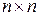 -матрицы неизвестных
-матрицы неизвестных
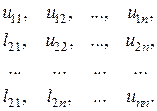 (5.8)
(5.8)
Специфика этой системы позволяет находить неизвестные (5.8) одно за другим в следующем порядке.
Из первой строки уравнений имеем
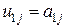
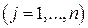 ;
;
из оставшейся части первого столбца уравнений
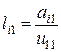
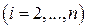 ;
;
из оставшейся части второй строки
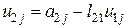
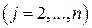 ;
;
из оставшейся части второго столбца
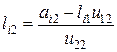
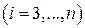
и т.д. Последним находится элемент
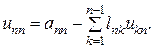
Легко видеть, что все отличные от 0 и 1 элементы матриц 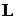 и
и 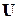 могут быть однозначно вычислены с помощью всего двух формул:
могут быть однозначно вычислены с помощью всего двух формул:
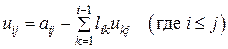 (5.9)
(5.9)
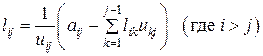 (5.10)
(5.10)
При практическом выполнении разложения матрицы 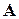 нужно иметь в виду следующие два обстоятельства:
нужно иметь в виду следующие два обстоятельства:
1. организация вычислений по формулам (5.9)-(5.10) должна предусматривать переключение счета с одной формулы на другую в соответствии с показанным выше процессом получения неизвестных, приведшим к этим формулам. Это удобно делать, ориентируясь на матрицу неизвестных (5.8), а именно, первая строка (5.8) вычисляется по формуле (5.9) при 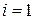 ,
, 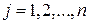 ; первый столбец (5.8) (без первого элемента) – по формуле (5.10) при
; первый столбец (5.8) (без первого элемента) – по формуле (5.10) при 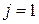 ,
, 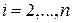 , и т. д.
, и т. д.
2. препятствием для осуществимости описанного процесса LU-разложения матрицы 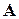 может оказаться равенство нулю диагональных элементов матрицы
может оказаться равенство нулю диагональных элементов матрицы 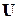 , поскольку на них выполняется деление по формуле (5.10). Отсюда требование теоремы, накладываемое на главные миноры.
, поскольку на них выполняется деление по формуле (5.10). Отсюда требование теоремы, накладываемое на главные миноры.
Заметим, что 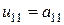 , т. е. первый диагональный элемент матрицы
, т. е. первый диагональный элемент матрицы  совпадает с первым минором
совпадает с первым минором  и по условию должен быть отличным от нуля. Второй диагональный элемент матрицы
и по условию должен быть отличным от нуля. Второй диагональный элемент матрицы 
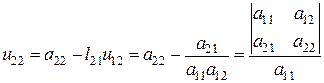
не равен нулю, если отличен от нуля второй главный минор, и т. д. Ясно, что вместо проверки на равенство нулю главных миноров данной матрицы удобнее делать такую проверку для элементов 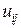 в процессе их вычисления, причем, чтобы уменьшить влияние погрешностей округлений, лучше сравнивать модули
в процессе их вычисления, причем, чтобы уменьшить влияние погрешностей округлений, лучше сравнивать модули 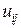 с малой положительной константой (допуском). Для определенных классов матриц требования теоремы о разложении заведомо выполняются. Это относится, например, к матрицам с диагональным преобладанием, т. е. к таким, для которых
с малой положительной константой (допуском). Для определенных классов матриц требования теоремы о разложении заведомо выполняются. Это относится, например, к матрицам с диагональным преобладанием, т. е. к таким, для которых
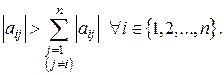
Если матрица 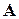 исходной системы (5.1) разложена в произведение треугольных
исходной системы (5.1) разложена в произведение треугольных 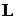 и
и 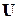 , то, значит, вместо (5.1а) можно записать эквивалентное (5.1) уравнение
, то, значит, вместо (5.1а) можно записать эквивалентное (5.1) уравнение
.
Введя вектор вспомогательных переменных 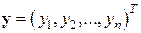 , последнее можно переписать в виде системы
, последнее можно переписать в виде системы
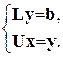
Таким образом, решение данной системы с квадратной матрицей коэффициентов свелось к последовательному решению двух систем с треугольными матрицами коэффициентов.
Получим сначала формулы для вычисления элементов 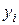 вспомогательного вектора
вспомогательного вектора 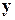 . Для этого запишем уравнение
. Для этого запишем уравнение 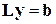 в развернутом виде:
в развернутом виде:
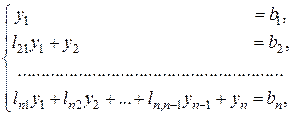
Очевидно, что все 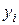 могут быть последовательно найдены при
могут быть последовательно найдены при 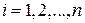 по формуле
по формуле
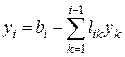 . (5.11)
. (5.11)
Развернем теперь векторно-матричное уравнение 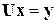 :
:
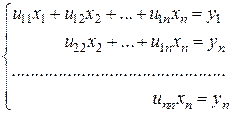 (5.12)
(5.12)
Отсюда значения неизвестных 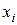 находятся в обратном порядке, т. е. при
находятся в обратном порядке, т. е. при 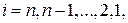 по формуле
по формуле
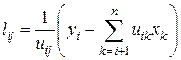 (5.13)
(5.13)
Решение линейных систем с помощью LU-разложения – это другая система реализации метода Гаусса. В отличие от рассмотренной в параграфе 5.1, так называемой, схемы единственного деления эту называют компактной схемой Гаусса или схемой Холецкого.
Вычисление определителя LU-факторизованной матрицы 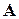 опирается на свойство определителя произведения матриц и сводится к перемножению
опирается на свойство определителя произведения матриц и сводится к перемножению  чисел:
чисел:
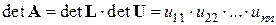
Для обращения матрицы 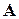 с помощью LU-факторизации можно применить тот же прием, который рассмотрен в параграфе 5.2, т.е.
с помощью LU-факторизации можно применить тот же прием, который рассмотрен в параграфе 5.2, т.е.  -кратно использовать формулы (5.11) и (5.13) для получения столбцов матрицы
-кратно использовать формулы (5.11) и (5.13) для получения столбцов матрицы 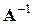 ; при этомв качестве
; при этомв качестве 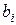 в (5.11) должны фигурировать только 0 или 1: для нахождения первого столбца
в (5.11) должны фигурировать только 0 или 1: для нахождения первого столбца 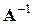 полагаем
полагаем 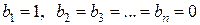 , для второго –
, для второго – 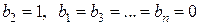 и т.д. Можно однако вывести и специальные формулы для выражения элементов обратной матрицы через элементы матриц
и т.д. Можно однако вывести и специальные формулы для выражения элементов обратной матрицы через элементы матриц 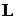 и
и 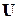 . Продемонстрируем это.
. Продемонстрируем это.
Пусть матрицы 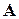 и
и 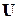 обратимы (матрица
обратимы (матрица 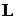 обратима всегда). Тогда
обратима всегда). Тогда
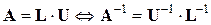
Умножая последнее равенство поочередно на 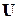 слева и на
слева и на 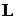 справа, будем иметь
справа, будем иметь
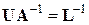 и
и 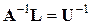 (5.14)
(5.14)
Анализ уравнений (5.14) позволяет выразить элементы 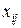 матрицы
матрицы 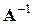 в виде
в виде
Чаще схемой Холецкого называют описываемый в следующем параграфе, основанный на той же идее способ решения симметричных линейных систем (метод квадратных корней).
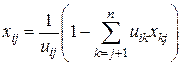 (5.15)
(5.15)
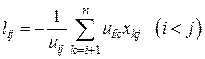 (5.16)
(5.16)
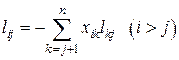 (5.17)
(5.17)
Схематично последовательность вычислений элементов обратной матрицы можно изобразить пронумерованными стрелками следующим образом:
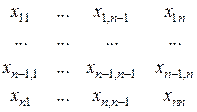
При этом стрелка 1 означает, что фиксируем 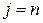 и ведем счет по формулам (5.15), (5.16) при
и ведем счет по формулам (5.15), (5.16) при 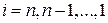 ; стрелка 2 – счет по формуле (5.17) при
; стрелка 2 – счет по формуле (5.17) при 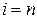 и
и 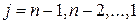 и т. д.
и т. д.
