Точки разрыва функции и их классификация

Определение 5.4.Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если х = х₀ – точка разрыва функции у = f(x), то в ней выполняется по крайней мере одно из условий непрерывности функции, а именно:

1) функция определена в окрестности точки х₀, но не определена в самой точке х₀. Например, функция у = 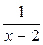не определена в точке х₀ = 2;

2) функция определена в точке х₀ и её окрестности, но не существует предела f(x) при х → х₀. Например, функция f(x) = 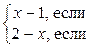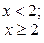определена в точке х₀ = 2, однако в точке х₀ = 2 имеет разрыв т. к. эта функция не имеет предела при х → 2: 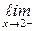f(x) = 1, а 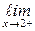f(x) = 0;

3) функция определена в точке х₀ и её окрестности, существует 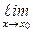f(x), но этот предел не равен значению функции в точке х₀: 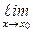f(x) ≠ f(x₀).

Например, функция f(x) =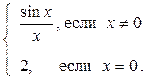

Здесь х₀ = 0 – точка разрыва: 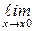f(x) = 1, а f(x₀) = 2.

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.

Точка разрыва х₀ называется точкой разрыва первого родафункции у = f(x), если в этой точке существуют конечные пределы функции слева и справа, т. е. 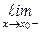f(x) = A₁ и 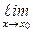f(x) = A₂. При этом:

а) если А₁ = А₂, то х₀ – точка устранённого разрыва;

б) если А₁ ≠ А₂, то х₀ – точка конечного разрыва.

Величина │А₁ − А₂│ называется скачком функции в точке разрыва первого рода.

Точка разрыва х₀ называется точкой разрыва второго родафункции у = f(x), если по крайней мере один из односторонних пределов не существует или равен бесконечности.

Пример 5.3. у = 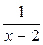, х₀ = 2 – точка разрыва второго рода.

Пример 5.4.f(x) = 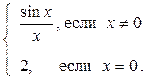х₀ = 0 – точка разрыва первого рода, скачок функции равен 1.

Пример 5.5.f(x) = 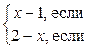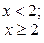х₀ = 0 является точкой устранимого разрыва первого рода.

Положив g(x) = 1 при х = 0, разрыв устранится, функция станет непрерывной.

Вопросы для самоконтроля

1. Сформулируйте определение непрерывной функции.

2. Какие арифметические действия не нарушает свойство непрерывности?

3. Какими свойствами обладает непрерывная на отрезке функция?

4. Дайте определение точек разрыва.

5. Дайте определение точек разрыва первого и второго рода.

Производная и дифференциал функции

Производная функции

Определение 6.1.Пусть на некотором промежутке 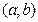определена функция у = f(x). Возьмём произвольную точку х₀ Î 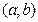и придадим аргументу х в точке х₀ произвольное приращение ∆х такое, что точка х₀ + ∆х Î 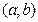. Производной функцииу = f(x) в точкех₀ называется предел при ∆х → 0 отношения приращения функции в этой точке к приращению аргумента, если этот предел существует. Обозначается предел функции f(x) в точке х₀ через f '(x₀), т. е.

f '(x₀) = = .

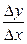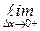
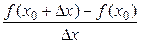Если функция у = f(x) имеет конечную производную в каждой точке х Î 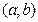, то производную f '(x) можно рассматривать как функцию от х, определённую на .

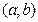Если для некоторого значения х₀ выполняется условие

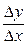= + ∞ (или = − ∞),

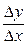то говорят, что в точке х₀ функция f(x) имеет бесконечную производнуюзнака плюс (или знака минус).

Пример 6.1.Найти производную функции f(x) = x² в точке х = х₀.

Решение.Придавая аргументу х в точке х₀ приращение ∆х, находим

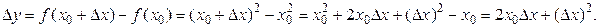
Тогда =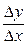

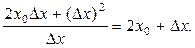
Теперь находим f '( ) = =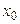

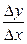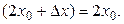
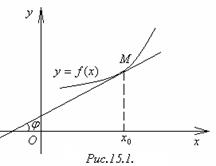Из школьного курса математики известно: геометрический смысл производнойсостоит в том, что производная функции f(x) в точке х₀ равна угловому коэффициенту касательной к графику функции f(x) в точке М(х₀; f(x₀)), т. е.

f '(x₀) = tgφ (рисунок 6.1).

Рисунок 6.1

Пример 6.2.Составить уравнение касательной, проведённой из точки М(1; −3) к параболе f(x) = x².

Решение.Пусть касательная в точке (х₀; f(x₀)) к параболе f(x) = x² имеет уравнение у = kx + b. Тогда по геометрическому смыслу касательной k = f '(x₀) = 2x₀. Так как касательная проходит через точки (1; −3) и (х₀; х₀²), то имеем систему:

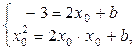
откуда, вычитая из второго уравнения первое, получим

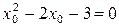
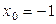или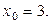

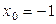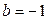Если , то и уравнение касательной имеет вид у = .

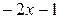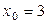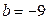Если , то и уравнение касательной – у = .

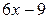Таблица производных

Таким образом можно составить таблицу производных простейших элементарных функций:

1. (C)' = 0, где С = const;

2. ( 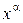)' = 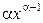. В частности ,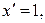

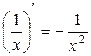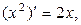
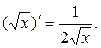
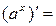
3. 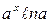. В частности, .

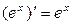4. 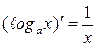× 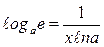. В частности,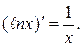

5.

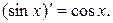
6.

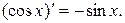
7. (tg )' .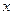

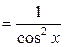8. (ctg )' .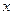

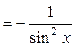9. .

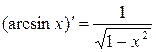10. .

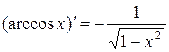11. (arctg )' .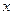

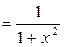12. (arcctg )' .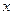

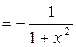Дифференциал функции

Определение 6.2.Функция у = f(x) называется дифференцируемой в точкех₀, если она имеет в этой точке конечную производную. Если функция дифференцируема в каждой точке интервала 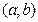, то она называется дифференцируемой на .

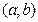В связи с этим определением операцию нахождения производной часто называют дифференцированием.

Если функция у = f(x) дифференцируема в точке х₀, то справедливы следующие утверждения:

1) ∆у = А × ∆х + α(∆х)∆х, где ∆х – приращение аргумента, ∆у – приращение функции, А – число, не зависящее от ∆х, α(∆х) – бесконечно малая функция при ∆х → 0. Очевидно, что А = 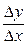= f '(x₀);

2) функция у = f(x) непрерывна в точке х₀.

Однако, не всякая непрерывная функция является дифференцируемой. Например, функция у = 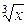непрерывна в точке х₀ = 0, т. к. 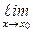f(x) = =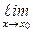 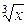= 0 = f(x₀).

Однако производная у' = ( 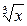)'= 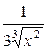в точке х₀ = 0 не существует, т. е. функция в точке х₀ = 0 не дифференцируема.

Определение 6.3.Пусть функция у = f(x) дифференцируема в точке х₀. Дифференциалом функцииf(x) в точке х₀ называется часть приращения функции

dy = f '(x₀) × ∆x.

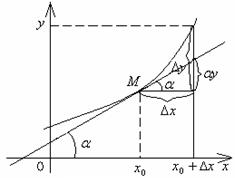Дифференциалом независимой переменнойх называется приращение этой переменной, т. е. dx = ∆x. Таким образом, геометрический смысл дифференциала функции у = f(x) состоит в том, что дифференциал dy в точке х₀ равен приращению ординаты касательной к графику этой функции в точке М(х₀; f(x₀)) (рисунок 6.2).

Рисунок 6.2

Во многих задачах приращение функции в данной точке можно приближённо заменить дифференциалом функции в этой точке: ∆у » dy.

Пример 6.3.Используя дифференциал функции, вычислить приближённо .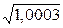

Решение.Пусть функция у = 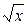. Положим 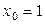и приращение аргумента 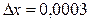. Тогда ∆у = 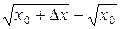» dy = y' 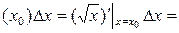= 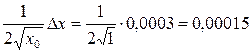. Теперь 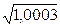» 1+ 0,00015 = 1,00015.

Правила дифференцирования функций сформулируем в следующей теореме.

Теорема 6.1. Если функции u = u(x) и v = v(x) дифференцируемы в точке х₀, то сумма, разность, произведение и частное этих функций (частное при условии, что v(x₀) ≠ 0) также дифференцируемы в этой точке, причём имеют место следующие формулы:

1) ;

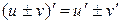2) ;

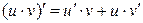3) .

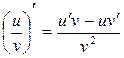Доказательство.Пусть функции u = u(x) и v = v(x) дифференцируемы в точке х₀:

1) =

= ±

± .

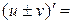
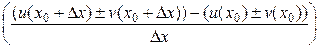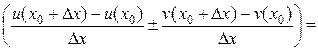
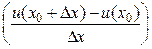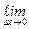
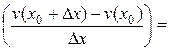
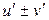2)

=

=

+ + = .

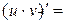
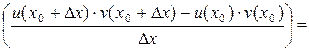
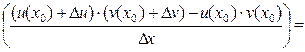
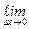
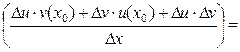
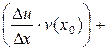
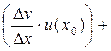
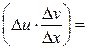
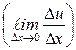
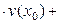
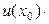
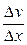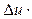
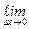
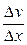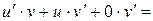
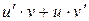3) Пусть .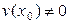

=

= .
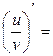
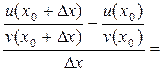
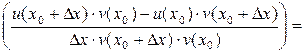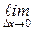
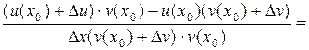
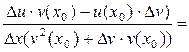
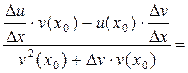
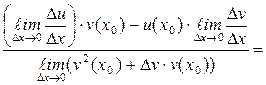
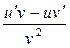