Идентификация порядка разности модели

На практике для выявления значений параметров p и q АРПСС модели используются автокорреляционные и частные автокорреляционные функции.

Шаг 1. Воспользуемся радом первых разностей (рисунок 7.2) и в окнеTransformations of Variables (Преобразование переменной) выберем вкладку Autocorrs (Автокорреляция).

Шаг 2.Для построения автокорреляционной функции необходимо выбрать кнопку Autocorrelations (Автокорреляция), при этом можно регулировать уровень значимости, указывая соответствующее значение в окне p-level for highlighting. В результате проведения процедуры получаем график представленный на рисунке 7.6.

Для расчета частной автокорреляционной функции выберем кнопку Partial autocorrelations, результаты представим на рисунке 7.7.

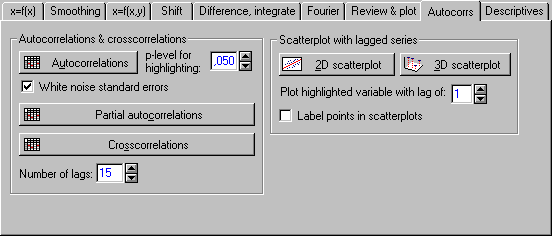
Рисунок 7.5 – Окно выбора расчета автокорреляционной, частной автокорреляционной функции и кросскорреляции (приведена часть исходного окна)

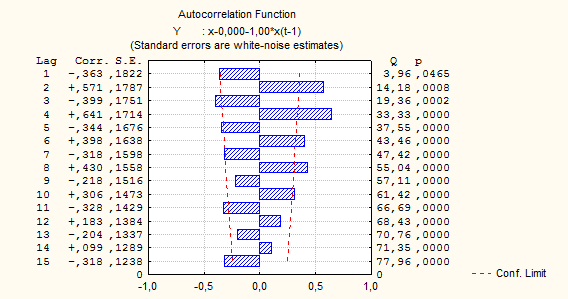
Рисунок 7.6 – Автокорреляционная функция

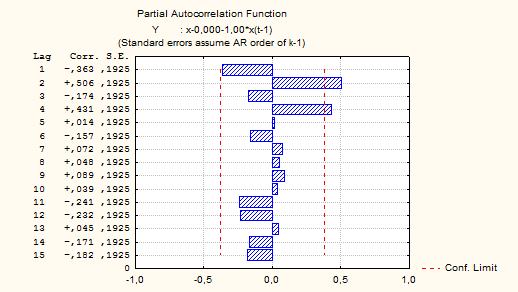
Рисунок 7.7 – Частная автокорреляционная функция

Обратимся к таблице 7.1 и попытаемся идентифицировать ARMA модель. Поведение автокорреляционной функции (экспоненциально затухает) согласуется с моделью ARMA (1,0) или ARMA (2,0). При этом поведение частной автокорреляционной функции (согласно рисунку 7.7, имеем выбросы на втором и четвертом лаге) не согласуется с данными моделями. Поэтому необходимо рассчитаем вторые разности, для этого во вкладке x=f(x) выбрать Autocorr. (x=x-(a+b*x(lag))), в качестве исходной переменной (в верхней части окна) выберем x-0,000-1,00*x(t-1)

Рисунок 7.8– Окно выбора исходной переменной для расчета (приведена часть исходного окна)

В результате получаем следующие автокорреляционные и частные автокорреляционные функции:

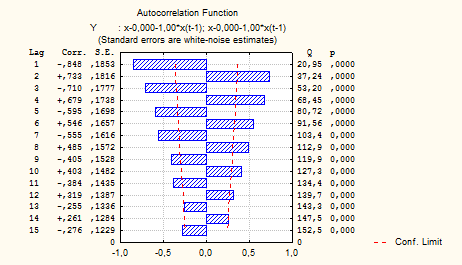
Рисунок 7.9 – Автокорреляционная функция

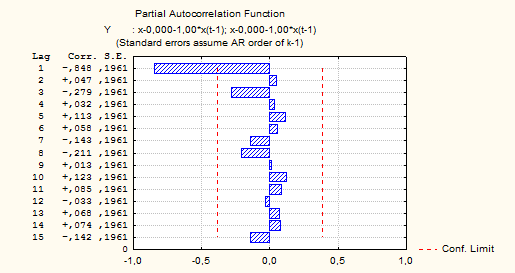
Рисунок 7.10 – Частная автокорреляционная функция

Полученные данные соответствуют модели ARMA(1,0), так как АКФ - экспоненциально затухает, ЧАКФ - выброс (пик) на лаге 1. После идентификации моделей перейдем к непосредственной оценки ее параметров.

Построение ARMA модели

В рассматриваемом пакете программ существует два метода построения авторегрессионных моделей:

1) Построение ARMA модели в модуле Multiple regression

2) Построение ARMA модели в модуле ARIMA & Autocorrelation function

7.7.1. Построение ARMA модели в модуле Multiple regression

Оценить параметры ARMA модели можно с помощью обычного МНК (но при этом оценки будут смещены). Для реализации этого метода в пакете необходимо:

Шаг 1. Сохранить результаты расчета вторых разностей, для этого в окне Transformations of Variables нажать кнопку Save variables получаем новую таблицу, содержавшую три переменные:

Y – исходный ряд денежного агрегата М0;

Y_1 – ряд первых разностей;

Y_2 – ряд вторых разностей.

Шаг 2. Проведем замену обозначений выведенных переменных: Y_1 засеменим на D’, Y_2 на D’’.

Также необходимо ввести переменную D’’t-1, для этого в главном меню выбираем Insert ® Add Variables. В появившемся окне Add Variables в поле Name заменим NewVar на D’’t-1, в поле Long name введем выражение =v3.

Шаг 3.Выбираем в главном меню Date ® Shift (Lag) и проводим сдвиг переменной D’’t-1 на один шаг вперед(Forward).

Шаг 4.В главном меню выбираем Statistics ® Multiple Regression. В окне Select dependent and independent variable lists (запускается после нажатия кнопки Variables) в качестве зависимой переменной указываем D’’ в качестве не зависимой - D’’t-1.

Шаг 5. Установим галочку возле опции Advanced options (stepwise or ridge regression) в появившемся окне Model Definition в прокрутке Intercept выберем Set to zero (т.е. регрессионное уравнение будет оценено без свободного члена). После оценки получим следующие результаты:

Таблица 7.2 – Результаты оценки модели вида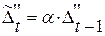

	Beta	Std.Err. of Betta	B	Std.Err. of B	t(24)	p-level
D''t-1	-0,878	0,098	-0,911	0,101	-8,992	0,000

Согласно результатам построения авторегрессионной модели вида ARMA(1,0), параметр a получен статистически значим. Также необходимо отметить, что модель статистически значима по F-критерию Фишера (F_факт(1,24)=80,86 против F_табл(1,24)= 4,26).

Шаг 6. В окне итогов построения регрессионной модели (Multiple Regression Results) необходимо выбрать вкладку Residuals / assumptions / prediction, далее кнопку .

В появившемся окне Residual Analysis выбираем вкладку Save ® Save residuals & predicted, в промежуточном окне Select variables to save with predicted/residual sc… выделим переменную D’’ и нажмем кнопку ОК. Получаем следующую таблицу с результатами:

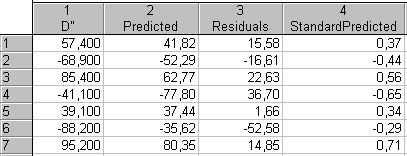
Рисунок 7.11 – Таблица результат оценки ARMA модели

Шаг 7. На основе полученной таблицы построим график. Выберем в главном меню Graphs ® 2D Graphs ® Line Plots (Variables…). Нажмем кнопку Variables (Переменные) и в появившемся окне укажем переменные D’’ и Predicted. Также в поле Graph type (окно 2D Line Plots –Variables) выделим Multiple (таким образом, на график будет выведены обе переменные одновременно).

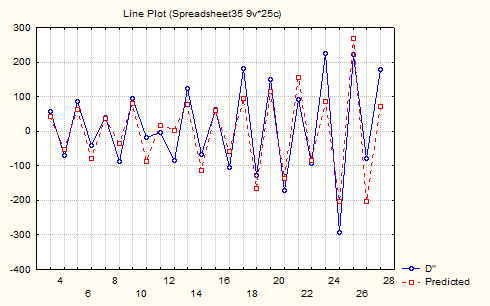
Рисунок 7.12 - Ряд вторых разностей денежного агрегата М0 и модельные данные

Согласно приведенному графику используемая для описания динамики первых разностей авторегрессионная модель ARMA (1,0) очень хорошо описывает анализимруемый ряд.

Шаг 8.Снова обратимся к вкладке Residuals/assumptions/prediction нажмем кнопку Predict dependent variable для прогнозирования уровней исследуемого ряда.

Шаг 9. В окне Specify values for indep. vars укажем последнее значение переменной D’’t-1 равное -79, получим следующий результат:

Таблица 7.3 – Точечный прогноз вторых разностей денежного агрегата М0 на 1 квартал 2006г.

	B-Weight	Value	B-Weight * Value
D''t-1	-0,911	-79,000	71,969
Predicted			71,969
-95,0%CL			55,451
+95,0%CL			88,488

Аналогичным образом рассчитаем значения для 2-4 квартала 2006г. при этом в качестве прогнозного значения будем использовать значение точечного прогноза предыдущего квартала:

Таблица 7.4 - Прогнозные значения вторых разностей денежного агрегата М0 на 2006г.

Квартал/год	Значения показателя для прогноза	Прогноз модели ARMA (1,0)	Нижняя доверительная граница	Верхняя доверительная граница
I/2006	-79,000	71,969	55,451	88,488
II/2006	71,969	-65,564	-80,612	-50,516
III/2006	-65,564	59,729	46,020	73,438
IV/2006	59,729	-54,413	-66,902	-41,924

7.7.2. Построение ARMA модели в модуле ARIMA & Autocorrelation function

Для построения семейства ARMA моделей в пакете STATISTICAсуществует специальный модуль:

Шаг 1. В главном меню выберем Statistics ® Advancer Linear/Nonlinear Models ® Time Series Analysis ® ARIMA & Autocorrelation function (Расчеты ® Основные линейные и нелинейные модели ® Анализ временных рядов ® ARIMA & Автокорреляционные функции).

Шаг 2. В появившемся окне Single Series ARIMA (АРПСС модель для одномерного ряда) выберем вкладку Quick (Быстрые). В верхней части окна выберем ряд, на основе которого будет проведена оценка модели, в нашем случае это – x-0,000-1,00*x(t-1); x-0,000-1,00*x(t-1) (ряд вторых разностей).

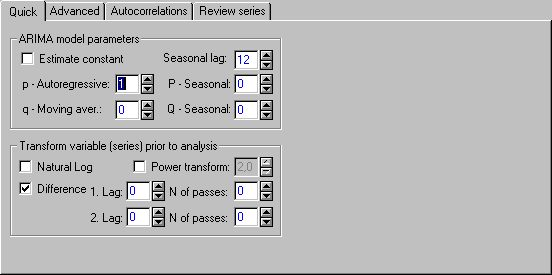
Рисунок 7.13 – Установки ARMA модели (приведено часть исходного окна)

Шаг 3. После нажатия кнопки будет выведено окно Single Series ARIMA Results (Результаты построения АРПСС модели для одномерного ряда).

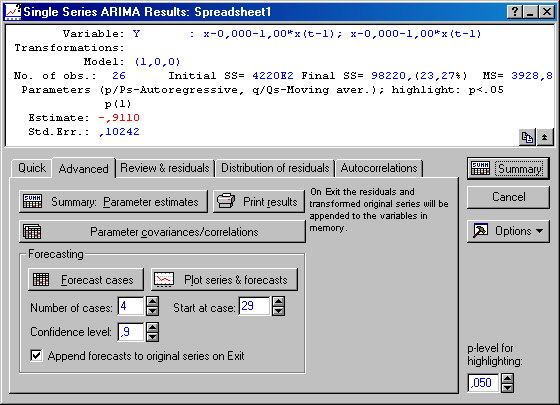
Рисунок 7.14 – Окно результатов построения АРПСС модели

Приведенное окно (рисунок 7.14) характерно для рассматриваемого пакета программ, оно разделено на две половины: в верхней части приведены результаты расчетов ARMA модели, в нижней части приведены вкладки, позволяющие подробнее просмотреть результаты построения модели и оценить прогноз.

Шаг 4. Выберем вкладку Advanced и нажмем кнопку Summary: Parameter estimates результаты приведем в таблице 7.5.

Таблица 7.5 – Результаты построения ARMA(1,0) модели

	Param.	Asympt. Std. Err.	Asympt. t(25)	p	Lower 95% Conf	Upper 95% Conf
p(1)	-0,911	0,102	-8,895	0,000	-1,122	-0,700

Во втором столбце расположены параметры уравнения в данном случае модель имеет вид:

В третьем столбце расположены асимптотические ошибки.

В четвертом асимптотический t-критерий.

Далее p-уровень значимости и 95% нижняя (верхняя) границы.

Судя по полученному значению асимптотического t-критерия полученная модель статистически значима.

Шаг 5. Для прогнозирования значений вторых разностей данном модуле необходимо во вкладке Advanced обратится к группе опций Forecasting (Прогнозирование). Допустим необходимо построить прогноз на 4 уровня вперед, для этого установим цифру 4 в опции Number of cases (Номер наблюдения). И нажмем кнопку Forecast cases (Прогноз значения), в результате получим таблицу 7.6 и рисунок 7.15.

Таблица 7.6 - Прогнозные значения вторых разностей денежного агрегата М0 на 2006г.

	Forecast	Lower 95%	Upper 95%	Std.Err.
	-162,614	-291,707	-33,522	62,680
	148,142	-26,487	322,772	84,791
	-134,958	-339,833	69,917	99,476
	122,947	-103,989	349,884	110,188

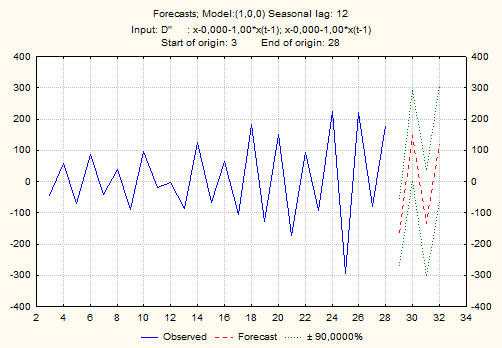
Рисунок 7.15 – Прогноз вторых разностей по модели ARMA (1,0)

Тесты для самоконтроля

1) Если автокорреляционная функция (АКФ) выказывает выброс на первом лаге, а частная автокорреляционная функция (ЧАКФ) экспоненциально затухает, то можно предположить что ряд наиболее адекватно опишет модель в форме:

а) ARMA(0,2)

б) ARMA(0,1)

в) ARMA(1,0)

2) Если АКФ экспоненциально затухает, а ЧАКФ обнаруживает выброс на первом лаге, то можно предположить что ряд наиболее адекватно опишет модель в форме:

а) ARMA(0,2)

б) ARMA(0,1)

в) ARMA(1,0)

3) Если АКФ экспоненциально затухает, а ЧАКФ обнаруживает выброс на первом и втором лаге, то можно предположить что ряд наиболее адекватно опишет модель в форме:

а) ARMA(2,0)

б) ARMA(0,1)

в) ARMA(1,0)

4) Если АКФ обнаруживает выбросы (пики) на лагах 1 и 2, а ЧАКФ экспоненциально затухает, то можно предположить что ряд наиболее адекватно опишет модель в форме:

а) ARMA(0,2)

б) ARMA(0,1)

в) ARMA(1,0)

5) Приведенная модель y_t = ay_t-1 + e_t является:

а) AR(1)

б) AR(2)

в) MA(1)

г) MA(2)

6) Приведенная модель y_t = a₁y_t-1 + a₂y_t-2 + e_t является:

а) AR(1)

б) AR(2)

в) MA(1)

г) MA(2)

7) Приведенная модель y_t = e_t +qe_t-1 является:

а) AR(1)

б) AR(2)

в) MA(1)

г) MA(2)

8) Приведенная модель y_t = e_t +q₁e_t-1 + q₂e_t-2 является:

а) AR(1)

б) AR(2)

в) MA(1)

г) MA(2)

9) Приведенная модель y_t = a₁y_t- + e_t +qe_t-1 является:

а) ARIMA (1, 1, 1)

б) ARMA (1, 1)

в) ARMA (2, 2)

10) Марковским процессом называют модель вида:

а) y_t = ay_t-1 + e_t

б) y_t = a₁y_t-1 + a₂y_t-2 + e_t

в) y_t = a₁y_t- + e_t +qe_t-1