Исключение результатов с грубыми погрешностями

Вопрос исключения грубых погрешностей или промахов по критериям решается статистическими методами, которые не применимы к однократным измерениям. Основная гипотеза заключается в том, что результат измерения не содержит грубой погрешности, то есть, является измеряемой величиной. Подтверждая или опровергая эту гипотезу, мы можем оценить результаты измерений.

Для исключения результатов с грубыми погрешностями будем использовать семь критериев: критерий Ирвина, критерий вариационного размаха, критерий граничной грубой погрешности, метод вычисления максимального относительного отклонения, метод Шарлье, критерий Романовского и критерий Шовене. Выбор критериев основан на законе распределения результатов наблюдений, представленного графически в приложении А (рисунок А.1).

Исключение грубых погрешностей выполняется для повышения точности результатов измерений.

1.2.1 Критерий Ирвина

Для полученных экспериментальных данных определяют коэффициент λ по формуле:

,

(1.7)

где , – наибольшие значения случайной величины;

– среднее квадратическое отклонение, вычисленное по всем значениям выборки.

Проводим проверку на наличие грубой погрешности для наибольшего значения выборки.

Наибольший результат: =11,700 мг/м³, =11,550 мг/м³,

мг/м³.

Затем этот коэффициент сравнивается с табличным значением , возможные значения которого приведены в таблице 3.1 [1].

мг/м³,

0,319<1,250,

т.е. λ< , нулевая гипотеза подтверждается, результат не является ошибочным и он не исключается при дальнейшей обработке результатов наблюдений.

Наименьший результат: = 10,000 мг/м³, = 10,050 мг/м³,

мг/м³.

Затем этот коэффициент сравнивается с табличным значением , возможные значения которого приведены в таблице 3.1[1].

мг/м³ ,

0,107<1,250,

т.е. λ< , нулевая гипотеза подтверждается, результат не является ошибочным и он не исключается при дальнейшей обработке результатов наблюдений.

1.2.2 Критерий вариационного размаха

Является одним из простых методов исключения грубой погрешности измерений (промаха). Для его использования определяют размах вариационного ряда упорядоченной совокупности наблюдений :

.

(1.8)

Если какой-либо член вариационного ряда, например , резко отличается от всех других, то производят проверку, используя следующее неравенство:

,

(1.9)

где – выборочное среднее арифметическое значение, вычисленное после исключения предполагаемого промаха;

– критериальное значение.

Для наибольшего значения: =11,700 мг/ м^3,

мг/м³,

=1,000,

,

9,006<11,700< 12,406.

Нулевая гипотеза (об отсутствии грубой погрешности) принимается, т.к. указанное неравенство (1,9) выполняется. Данное значение не является грубой погрешностью.

Для наименьшего значения: =10,000 мг/м³,

мг/м³,

=1,000,

,

10,706=10,706˃10,000.

Нулевая гипотеза (об отсутствии грубой погрешности) не принимается, т.к. указанное неравенство не выполняется. Данное значение является грубой погрешностью.

1.2.3 Критерий граничной грубой погрешности

Воспользуемся критерием грубой погрешности «k» , зависящим от объема выборки n и принятой доверительной вероятности Р, где:

n=25,

Р=0,95,

k=2,505,

. (1.10)

Если для указанное выше неравенство выполняется, то исключается из полученного ряда измерений.

Проверим подтверждение нулевой гипотезы для наибольшего и наименьшего значений выборки.

Для наименьшего: = 10,000 мг/м³,

,

.

Нулевая гипотеза не подтвердилась, данное значение не является грубой погрешностью.

Для наибольшего: =11,700 мг/м³,

,

.

Нулевая гипотеза не подтвердилась, данное значение не является грубой погрешностью.

1.2.4 Метод вычисления максимального относительного отклонения

Статистический критерий обнаружения грубых погрешностей основан на предположении, что выборка взята из генеральной совокупности, распределенной нормально. Это позволяет использовать распределение наибольшего по абсолютному значению нормированного отклонения:

Для уровней значимости р ≥0,10; 0,05; 0,01 или доверительной вероятности

Р=1 – р , равной 0,90; 0,95; 0,99 и количества результатов n от 3 до 25 значения (P; n) приведены в таблице 3.7 [1].

Согласно данному методу необходимо:

– вычислить критерий, определяющий меру отклонения от среднего арифметического проделанного ряда измерений:

(1.11)

– по таблице квантилей распределения статистики определить граничное значение критерия (P;n), соответствующее выбранному доверительному уровню вероятности Р и числу проделанных измерений n (таблица 3.7 [1]);

– результат исключают, если Вероятность Р характеризует степень надежности вывода о необходимости исключения результата ;

– пересчитать и для оставшихся результатов измерений n-1;

– повторить процедуру отсева для следующего максимального относительного отклонения.

И если то результат с вероятностью Р содержит грубую погрешность и его следует исключить из дальнейшей обработки

Проводим проверку на наличие грубой погрешности для крайних значений выборки:

Для наименьшего результата: = 10,000 мг/м³,

=2,720 мг/м³;

17,591˃2,720.

Т.к. то результат с вероятностью Р содержит грубую погрешность и его следует исключить из дальнейшей обработки.

Для наибольшего результата: х₂₅ = 11,700 мг/м³,

=2,720 мг/м³;

24,768˃2,720.

Т.к. то результат с вероятностью Р содержит грубую погрешность и его следует исключить из дальнейшей обработки.

1.2.5 Метод Шарлье

Метод Шарлье основан на теореме Бернулли, утверждающей, что число результатов измерений, удовлетворяющих условию:

, (1.12)

равно n[1-Ф(К_ш)], где Ф(К_ш) – значение нормированной функции Лапласа. Приведем некоторые значения коэффициента Шарлье в зависимости от n.

Если для указанное выше неравенство выполняется, то исключается из полученного ряда измерений.

Для наибольшего значения: =11,700 мг/ м³,

=1,875,

,

.

Условие выполняется, следовательно наибольшее значение является грубой погрешностью.

Для наименьшего значения: = 10,000 мг/ м³,

=1,875,

,

.

Условие не выполняется, следовательно наименьшее значение не является грубой погрешностью.

1.2.6 Критерий Романовского

По таблице 3.2 [1] находим коэффициент Стьюдента. При числе степеней свободы и доверительной вероятности 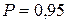, . Гипотеза о наличии грубых результатов подтверждается, если выполняется следующее условие:

(1.13)

Проводим проверку на наличие грубой погрешности для крайних значений выборки.

Для наименьшего результата: _.= 10,000 мг/м³,

,

.

Неравенство не выполняется, следовательно, =10,000 мг/м³ не является грубой погрешностью.

Для наибольшего результата: =11,700 мг/м³,

,

.

Неравенство выполняется, следовательно, =11,700 мг/м³ является грубой погрешностью.

1.2.7 Критерий Шовене

Критерий Шовене применяется для всех законов распределения, и строится на определении числа ожидаемых результатов наблюдений , которые имеют столь же большие погрешности, как и подозрительный. Гипотеза о наличии грубой погрешности принимается, если выполняется условие:

.

Порядок проверки гипотезы следующий:

1) вычисляются среднее арифметическое и СКО результатов наблюдений для всей выборки;

2) из таблицы нормированного нормального распределения (Приложение В – интегральная функция нормированного нормального распределения [1]) по величине определяется вероятность появления подозрительного результата в генеральной совокупности чисел n:

;

(1.14)

3) число ожидаемых результатов определяется по формуле:

;

(1.15)

Проводим проверку на наличие грубой погрешности для крайних значений выборки.

Для наименьшего результата: = 10,000 мг/м³,

.

По таблице В.1 Приложения В [1] определяем вероятность выхода результатов за квантиль .

.

Тогда ожидаемое число наблюдений с результатом мг/м³.

.

Так как , то приходим к выводу, что результат наблюдений мг/м³ не является грубой погрешностью.

Для наибольшего результата: =11,700 мг/м³,

.

По таблице В.1 Приложения В [1] определяем вероятность выхода результатов за квантиль :

.

Тогда ожидаемое число наблюдений с результатом мг/м³,

.

Так как , то приходим к выводу, что мг/м³ не является грубой погрешностью.

Поскольку большинство критериев показали, что в проверяемых на наличие грубых погрешностей результатах наблюдений =10,000 мг/м³ и =11,700 мг/м³ – гипотезы о наличие грубых погрешностей не подтвердились, то при дальнейшей обработке результатов наблюдений они не исключаются из совокупности первоначальных результатов.