Класифікація алгебраїчних рівнянь

Рівняння f(х) = φ(х) називається алгебраїчним, якщо f(х), φ(х) — алгебраїчні функції. До алгебраїчних функцій належать, наприклад, цілі раціональні функції (багаточлени), дробово-раціональні функції (відношення двох багаточленів), ірраціональні функції.

Приклади алгебраїчних рівнянь: 2х+5=1, х²-х-1=0, х³-Зх=0,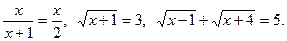

Рівняння f(х) = φ(х) називається раціональним, якщо f(х), φ(х) — багаточлени.

Рівняння f(х) = φ(х) називається дробово-раціональним,
якщо f(х), φ(х) — раціональні функції, причому хоча б одна
з них дробово-раціональна відносно змінної х.

Рівняння f(х) = φ(х) називається ірраціональним, якщо
f(х), φ(х) — елементарні алгебраїчні функції й хоча б
одна з них ірраціональна відносно змінної х.

Рівняння f(х) = φ(х) називається елементарним трансцендентним, якщо f(х), φ(х)— елементарні функції й хоча б
одна з них трансцендентна відносно змінної х.

Приклади алгебраїчних рівнянь різного виду:

1) х-7 = 2, х² -х = 0, х⁵-3 = 0 — раціональні рівняння з одною невідомою;

2) х²-у² = х-у — раціональне рівняння із двома невідомими;

3) 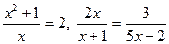дробно-раціональні;

4) 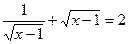— ірраціональне рівняння;

5) 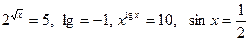— трансцендентне
рівняння.