Ряды в комплексной области.

Существование понятия предела последовательности (1.5) позволяет рассматривать ряды в комплексной области (как числовые, так и функциональные). Стандартно определяются частичные суммы, абсолютная и условная сходимость числовых рядов. При этом сходимость ряда предполагает сходимость двух рядов, один из которых состоит из действительных, а другой из мнимых частей членов ряда: 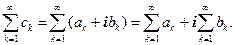Например, ряд 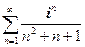сходится абсолютно, а ряд 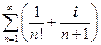− расходится (за счет мнимой части).

Если действительная и мнимая части ряда сходятся абсолютно, то абсолютно сходится и сам

ряд, т.к. 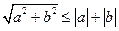. Верно и обратное: из абсолютной сходимости комплексного ряда

следует абсолютная сходимость действительной и мнимой части: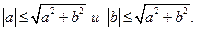

Аналогично функциональным рядам в действительной области определяются комплексные

функциональные ряды, область их поточечной и равномерной сходимости. Без изменения

формулируется и доказывается признак Вейерштрасса равномерной сходимости. Сохраняются

все свойства равномерно сходящихся рядов.

При исследовании функциональных рядов особый интерес представляют собой степенные

ряды: 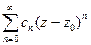, или после замены 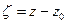: 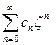. Как и в случае действительной

переменной, верна теорема Абеля: если степенной ряд (последний) сходится в т. ζ₀ ≠ 0, то он сходится, и притом абсолютно, для любого ζ , удовлетворяющего неравенству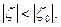

Таким образом, область сходимости D этого степенного ряда представляет собой круг радиуса R с центром в начале координат, где R − радиус сходимости − точная верхняя грань значений 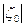(Откуда и появился этот термин). Исходный степенной ряд будет, в свою очередь, сходиться в круге радиуса R с центром в т. z₀ . При этом, в любом замкнутом круге 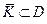степенной ряд сходится абсолютно и равномерно (последнее утверждение сразу следует из признака Вейерштрасса (см. курс “Ряды”)).

Пример. Найти круг сходимости и исследовать на сходимость в тт. z₁ и z₂ степенного ряда 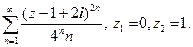Решение. 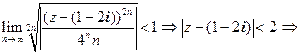область сходимости − круг радиуса R = 2 с центром в т. z₀ = 1 − 2i . 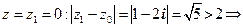z₁ лежит вне круга сходимости и ряд расходится. При 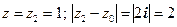, т.е. точка лежит на границе круга сходимости. Подставив ее в исходный ряд, заключаем:

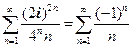− ряд сходится условно по признаку Лейбница.

Если во всех граничных точках ряд сходится абсолютно или расходится по необходимому признаку, то это можно установить сразу для всей границы. Для этого следует подставить в ряд

из модулей слагаемых значение R вместо выражения 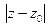и исследовать полученный ряд.

Пример. Рассмотрим ряд из последнего примера, изменив один сомножитель: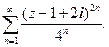

Область сходимости ряда осталась прежней: 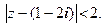Подставим в ряд из модулей

полученный радиус сходимости:

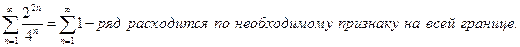
Если обозначить сумму ряда 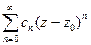через f(z), т.е. f(z) = 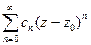(естественно, в

области сходимости), то этот ряд называют рядом Тейлора функции f(z) или разложением функции f(z) в ряд Тейлора. В частном случае, при z₀ = 0, ряд называется рядом Маклорена функции f(z) .

1.7 Определение основных элементарных функций. Формула Эйлера.

Рассмотрим степенной ряд 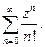Если z − действительная переменная, то он представляет

собой разложение функции 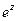в ряд Маклорена и, следовательно, удовлетворяет

характеристическому свойству показательной функции: 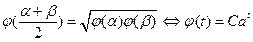, т.е. 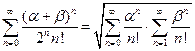. Это и является основанием для определения экспоненциальной функции в комплексной области :

Определение 1. .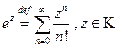

Аналогично определяются функции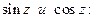

Определение 2.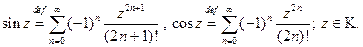

Все три ряда сходятся абсолютно и равномерно в любой ограниченной замкнутой области комплексной плоскости.

Из трех полученных формул простой подстановкой выводится формула Эйлера:

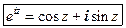
Отсюда сразу получается показательная форма записи комплексных чисел:

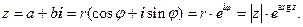
Формула Эйлера устанавливает связь между обычной и гиперболической тригонометрией.

Рассмотрим, например, функцию 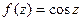: 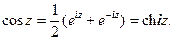Аналогично получаются остальные соотношения. Итак:

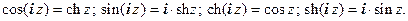
Примеры. Представить указанные выражения в виде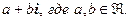

1.

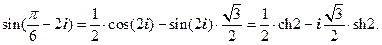
2. 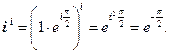(выражение в скобках представляет собой число i , записанное в показательной форме)

3.

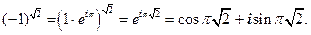
4. Найти линейно независимые решения линейного ДУ 2 – го порядка: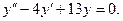

Корни характеристического уравнения равны:

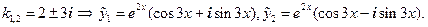
Так как мы ищем действительные решения уравнения, то в качестве фундаментальной системы решений можно взять функции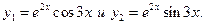

Определим, в заключение, логарифмическую функцию комплексной переменной. Как и в действительной области, будем считать ее обратной к показательной. Для простоты рассмотрим только экспоненциальную функцию, т.е. решим уравнение 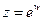относительно w , которую и назовем логарифмической функцией. Для этого прологарифмируем уравнение, представив z в показательной форме:

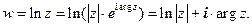
Если вместо arg z написать Arg z (1.2), то получим бесконечнозначную функцию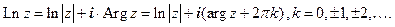

1.8 Производная ФКП. Аналитические функции. Условия Коши – Римана.

Пусть w = f (z) – однозначная функция, определенная в области .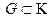

Определение 1. Производнойот функции f (z) в точке называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:

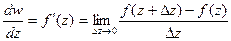
Функция, имеющая производную в точке z, называется дифференцируемой в этой точке.

Очевидно, что выполняются все арифметические свойства производных.

Пример.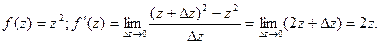

С помощью формулы бинома Ньютона аналогично выводится, что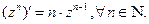

Ряды для экспоненты, синуса и косинуса удовлетворяют всем условиям почленного дифференцирования. Непосредственной проверкой легко получить, что:

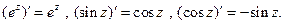
Замечание. Хотя определение производной ФКП формально полностью совпадает с определением для ФДП, но, по существу, является более сложным (см. замечание в п. 1.5).

Определение 2. Функция f (z) , непрерывно дифференцируемая во всех точках области G, называется аналитическойили регулярнойв этой области.

Теорема 1. Если функция f (z) дифференцируема во всех точках области G, то она является аналитической в этой области. (б/д)

Замечание. Фактически, эта теорема устанавливает эквивалентность регулярности и дифференцируемости ФКП на области.

Теорема 2. Функция, дифференцируемая в некоторой области, имеет бесконечно много производных в этой области. (б/д. Ниже ( в п.2.4 ) это утверждение будет доказано при определенных дополнительных допущениях)

Представим функцию в виде суммы действительной и мнимой частей: 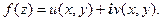Теорема 3. ( Условия Коши − Римана).Пусть функция f (z) дифференцируема в некоторой точке 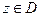. Тогда функции u (x,y) и v (x,y) имеют в этой точке частные производные, причем

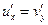и 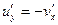, называемые условиями Коши – Римана.

Доказательство. Так как значение производной не зависит от способа стремления величины

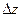к нулю, выберем следующий путь: 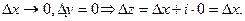Получаем:

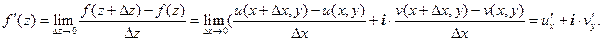
Аналогично, при 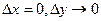имеем: 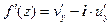, что и доказывает теорему.

Верно и обратное утверждение:

Теорема4. Если функции u (x,y) и v (x,y) имеют в некоторой точке непрерывные частные производные, удовлетворяющие условиям Коши – Римана, то сама функция f (z) – дифференцируема в этой точке. (б/д)

Теоремы 1 – 4 показывают принципиальное отличие ФКП от ФДП.

Теорема 3 позволяет вычислять производную функции по любой из следующих формул:

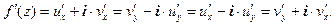
При этом можно считать х и у произвольными комплексными числами и вычислять производную по формулам: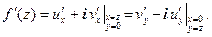

Примеры. Проверить функцию на регулярность. Если функция регулярна – вычислить ее производную.

1.

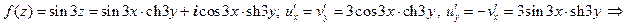
функция регулярна;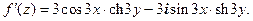

2. 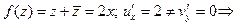функция не дифференцируема.

Замечание. Нетрудно видеть, что любая действительная функция комплексного аргумента – не дифференцируема.

1.9 Гармонические функции.

Напомним определение гармонических функций, данное в курсе «Теории поля» :

Определение. Функция u (x,y) называется гармонической, если она удовлетворяет уравнению Лапласа: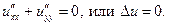

Пусть на области G задана аналитическая функция 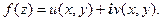Эта функция удовлетворяет условиям Коши – Римана: 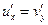, 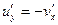(п. 1.8). Так как аналитическая функция бесконечно дифференцируема, то и функции u и v так же бесконечно дифференцируемы. Продифференцируем первое условие по x , второе по y и сложим полученные равенства:

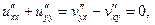т.е. действительная часть аналитической функции – гармоническая. Если условия продифференцировать по у , по х и вычесть, то легко убедиться в гармоничности мнимой части. Таким образом, доказана

Теорема. Действительная и мнимая части аналитической функции являются гармоническими:

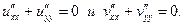
Ясно, что две произвольные гармонические функции, вообще говоря, не будут действительной и мнимой частями некоторой аналитической функции. Для этого они должны еще удовлетворять условиям Коши – Римана. Однако, по любой гармонической функции можно с точностью до константы определить вторую часть аналитической функции (т.е. саму аналитическую функцию).

Пример. Доказать, что 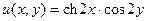может быть действительной частью аналитической функции и определить эту функцию.

Решение. 1.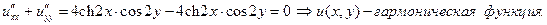

2.

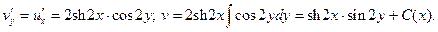
Из 2-го условия К – Р: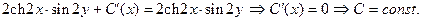

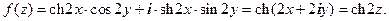
Вопросы для самопроверки.

1.Являются ли следующие множества точек областями?

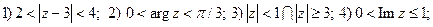
2. Записать комплексные числа в тригонометрической и показательной форме.

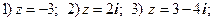
3. Доказать тождество: .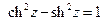

4. Является ли функция 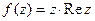аналитической?