Неньютоновские вязкие жидкости
а) Вязкопластичные жидкости. Реологическое уравнение вязкопластичной жидкости в случае одномерного течения можно записать в виде
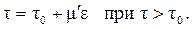
При 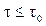 текучесть отсутствует, то есть среда ведет себя как твердое тело.
текучесть отсутствует, то есть среда ведет себя как твердое тело.
Здесь 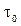 - предельное напряжение сдвига,
- предельное напряжение сдвига, 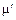 - пластическая или структурная вязкость. Согласно этой модели (Бингама - Шведова) среда не деформируется при
- пластическая или структурная вязкость. Согласно этой модели (Бингама - Шведова) среда не деформируется при 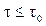 . Затем деформация происходит так же как в ньютоновской жидкости, но под действием напряжения, уменьшенного на величину
. Затем деформация происходит так же как в ньютоновской жидкости, но под действием напряжения, уменьшенного на величину 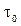 .
.
Физическое объяснение свойств таких сред – наличие в них при покое некоторой пространственной жесткой структуры, которая сопротивляется любому внешнему воздействию пока вызванное им напряжение сдвига не превзойдет соответствующее этой структуре предельное напряжение. После этого структура полностью разрушается и система вдет себя как обычная ньютоновская жидкость при напряжениях сдвига 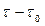 . Структура снова восстанавливается, когда действующие в жидкости напряжения сдвига становятся меньше
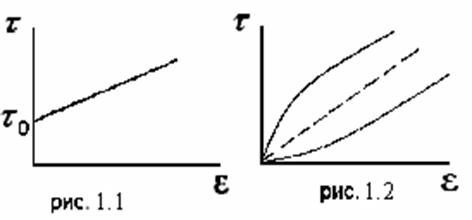
. Структура снова восстанавливается, когда действующие в жидкости напряжения сдвига становятся меньше 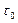 . Таким образом, сдвиговое течение вязкопластичных жидкостей характеризуется образованием квазитвердых участков в тех местах потока, где касательные напряжения ниже предела текучести. Кривая течения вязкопластичных жидкостей представлена на рис. 1.1. Модель вязкопластичной жидкости используется для описания поведения глинистых растворов, ряда нефтей, шламов, масляных красок.
. Таким образом, сдвиговое течение вязкопластичных жидкостей характеризуется образованием квазитвердых участков в тех местах потока, где касательные напряжения ниже предела текучести. Кривая течения вязкопластичных жидкостей представлена на рис. 1.1. Модель вязкопластичной жидкости используется для описания поведения глинистых растворов, ряда нефтей, шламов, масляных красок.
б) Степенные жидкости. Реологическое уравнение в случае одномерного течения: 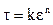 . Это нелинейно – вязкие жидкости с нелинейной кривой течения, проходящей через начало координат. В зависимости от хода кривой течения относительно осей
. Это нелинейно – вязкие жидкости с нелинейной кривой течения, проходящей через начало координат. В зависимости от хода кривой течения относительно осей 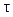 и
и 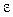 возможны два типа таких жидкостей: псевдопластичные, для которых
возможны два типа таких жидкостей: псевдопластичные, для которых 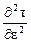 < 0 и дилатантные для которых
< 0 и дилатантные для которых 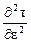 > 0. (рис. 1.2). Удобной характеристикой поведения таких жидкостей служит кажущаяся вязкость
> 0. (рис. 1.2). Удобной характеристикой поведения таких жидкостей служит кажущаяся вязкость 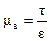 . У псевдопластичных жидкостей
. У псевдопластичных жидкостей 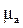 постепенно уменьшается, у дилатантных возрастает.
постепенно уменьшается, у дилатантных возрастает.
Кривая течения имеет линейный участок при небольших скоростях сдвига и при очень больших величинах скоростей сдвига. Соответствующие вязкости обозначаются через μо и μ∞.
Величина k называется консистентностью, n –индекс течения. При n < 1 жидкость называется псевдопластичной, при n > 1 – дилатантной.
Важно иметь в виду, что хотя во многих случаях значение n приблизительно постоянно в довольно широких пределах изменения скорости сдвига, в реальной жидкости, если рассматривать весь возможный диапазон напряжений сдвига, это не имеет места. Но в инженерной практике, в частных задачах, реологическое уравнение описывает жидкость в ограниченном диапазоне скоростей сдвига. В этих пределах n можно считать постоянным. Размерность k зависит от показателя степени n.
Псевдопластичностью, например, обладают суспензии с асимметричными частицами. Наиболее распространенное физическое объяснение поведения псевдопластичной среды сводится к следующему. Предполагается, что с возрастанием скорости сдвига асимметричные частицы или молекулы постепенно своими большими осями ориентируются вдоль направления потока. Кажущаяся вязкость будет убывать с ростом скоростей сдвига до тех пор, пока сохраняется возможность дальнейшего ориентирования частиц вдоль линий тока, а затем кривая течения становится линейной. К псевдопластичным жидкостям относятся растворы и расплавы высокополимеров.
Дилатантное поведение было впервые обнаружено Рейнольдсом в суспензиях с большим содержанием твердой фазы. Он предположил, что в состоянии покоя эти суспензии имеют минимальный объем прослоек между твердыми частицами и жидкости хватает как раз только для заполнения этих прослоек. Когда материал подвергается сдвигу с небольшой скоростью деформации, жидкость служит смазкой и напряжения, следовательно, невелики. С ростом скорости сдвига материал разбухает, плотная упаковка частиц нарушается и жидкости становится недостаточно для смазки трущихся друг о друга частиц и действующие напряжения значительно возрастают.
Многие жидкости, например, крахмальные пасты, не относятся к таким суспензиям и не расширяются при сдвиге. Тем не менее, они обнаруживают дилатансию.
