Основы теории погрешностей.
Примеры решения задач
Задача 1
В цепи, содержащей идеальный источник напряжения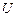 
(внутреннее сопротивление 
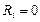) и сопротивление нагрузки 
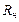, измеряется сила тока амперметром с внутренним сопротивлением 
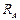. Амперметр измеряет силу тока абсолютно точно.
Определить абсолютную и относительную погрешность измерения тока за счет конечного значения 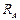. Классифицировать измерение и погрешность измерения. Определить величину поправки, необходимой для устранения погрешности измерения.
Решение задачи
По определению абсолютная погрешность измерения
.
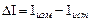В данном случае видно, что
,
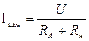а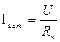 
(ток, который протекал в цепи до включения в нее амперметра), тогда 
.
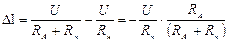Относительная погрешность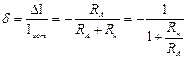 
.
Отсюда следует общеизвестный вывод: для обеспечения малой методической погрешности измерения амперметр должен обладать малым сопротивлением, т.е. должно выполняться условие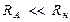 
.
Погрешность измерения является в данном случае методической, т.к. обусловлена неидеальностью метода измерения (по условию задачи амперметр измеряет силу тока абсолютно точно, т.е. инструментальные погрешности отсутствуют); систематической (т.к. при многократных измерениях погрешность остается постоянной). Само измерение можно классифицировать как прямое, непосредственной оценки, абсолютное, однократное, статическое.
Поправка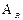 
, необходимая для устранения систематической погрешности, представляет собой абсолютную погрешность, взятую с противоположным знаком, т.е.
.
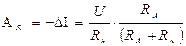Задача 2
Миллиамперметр с пределом измерения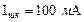 
показал результат измерения тока 
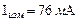. При этом известно, что действительное значение 
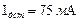. Определить абсолютную, относительную и приведенную погрешности измерения.
Решение задачи
Известно, что абсолютная погрешность 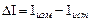, но т.к. истинное значение ФВ мы никогда не можем знать, то в метрологии истинное значение при всех вычислениях заменяют действительным значением, т.е.
.
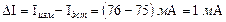Относительная погрешность
.
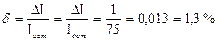Приведенная относительная погрешность по определению: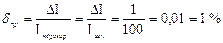 
.
Задача 3
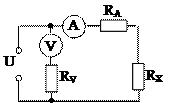
Методом амперметра-вольтметра по приведенной схеме измеряется сопротивление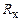 
. Показания приборов:
.
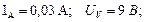
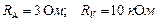Определить:
1) результат измерения;
2) абсолютную и относительную методические погрешности измерения;
3) исправленный результат измерения.
Решение задачи
Результат измерения в соответствии с указанным методом определяется на основании закона Ома по показаниям приборов
.
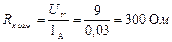Абсолютная методическая погрешность измерения
,
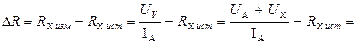
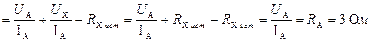где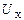 
и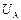 
- падения напряжения на 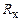и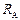 
соответственно, а 
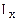- ток через .
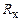Относительная методическая погрешность измерения
.
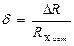Найдем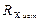 
, это исправленный результат измерения с учетом внесенной поправки 
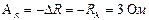, тогда
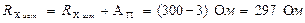и
.
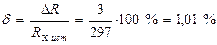Задача 4
При обработке результатов измерений напряжения получены следующие оценки погрешности: систематическая погрешность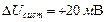 
; среднеквадратическая погрешность 
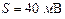. Случайная погрешность распределена по нормальному закону.
Определить вероятность того, что результат измерения отличается от истинного значения ФВ не более чем на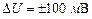 
. Решить задачу для двух случаев:
1) систематическая погрешность из результата измерения не устраняется;
2) систематическая погрешность устраняется.
Решение задачи
1) Первый вариант задачи.
Понятно, что истинное значение измеряемой величины имеет погрешность, равную нулю, т.е. необходимо определить вероятность попадания погрешности в интервал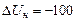 
, 
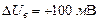относительно нуля. Кроме того, известно, что систематическая погрешность представляет собой математическое ожидание реального закона распределения погрешности, т.е. 
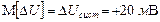. Вероятность попадания в требуемый интервал определяется выражением
,
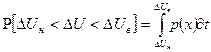а для нормального закона распределения
,
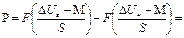
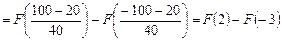где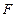 
- интегральная функция нормированного нормального распределения. Из соответствующей таблицы 1 Приложения найдем, что 
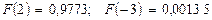, тогда
.
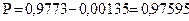21) Второй вариант задачи.
При устранении систематической погрешности математическое ожидание становится равным нулю, т.е.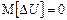 
и интервал становится симметричным, т.е. 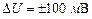. Тогда
.
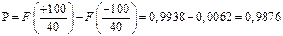Задача 5
При измерении сопротивления получены следующие оценки результата измерения и погрешностей: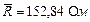 
, составляющие НСП 
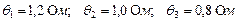, составляющие нормально распределенной случайной погрешности 
.
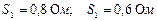Записать результат измерения при доверительной вероятности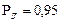 
.
Решение задачи
Для определения общей погрешности измерения необходимо просуммировать отдельно составляющие систематической погрешности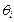 
, отдельно составляющие случайной погрешности 
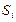и затем сложить полученные суммарные значения НСП и случайной погрешности в соответствии с правилами суммирования погрешностей. Тогда границы систематической погрешности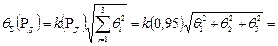 
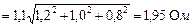, а СКП систематической погрешности
.
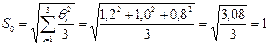В условии задачи отсутствует указание величин коэффициента корреляции, следовательно, составляющие случайной погрешности некоррелированы (независимы) и суммарная СКП:
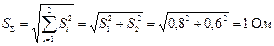
Границы доверительного интервала случайной погрешности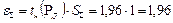 
, где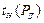 
- коэффициент нормального закона распределения.
Далее необходимо сложить систематическую и случайные составляющие погрешности. Сначала определяем соотношение
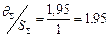, т.е. 
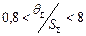. Тогда
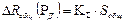, где 
.
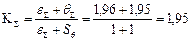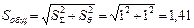и
.
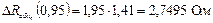Результат измерения с учетом правил округления погрешности и результата запишется в следующем виде
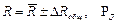, т.е.
.
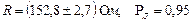Задача 6
Проведено 10 измерений емкости конденсатора. Получена оценка математического ожидания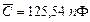 
; СКП отдельного измерения 
. Определить границы доверительного интервала погрешности при доверительной вероятности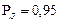 
. Записать результат измерения.
Решение задачи
Границы доверительного интервала погрешности результата многократных измерений при заданно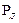й 
и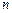 
определяются выражением
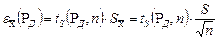, где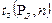 
- коэффициент Стьюдента, (находится из таблицы Приложения); 
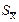- СКП результата измерения; 
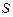- СКП отдельного измерения. Применительно к нашей задаче имеем
, 
.
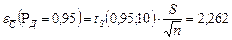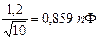Результат измерения может быть записан в следующем виде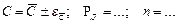 
, тогда с учетом правил округления погрешности и результата измерения
.
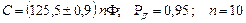