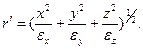Условия на границе раздела двух сред
Рассмотрим поведение электромагнитного поля при переходе через границу раздела двух сред с различными материальными характеристиками. Используем теорему Остроградского-Гаусса и теорему Стокса:
Теорема Остроградского-Гаусса:
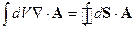
т.е. совершается следующий переход:
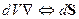
Теорема Стокса:
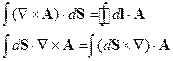
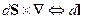
Запишем первое и четвёртое уравнения Максвелла в среде:
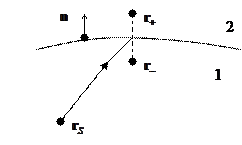
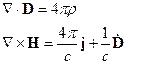
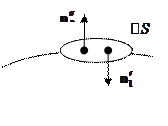
Имеется граница раздела – поверхность, отделяющая одну среду от другой.
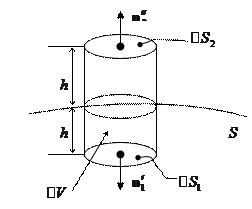
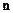- нормаль к поверхности.
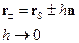
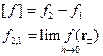
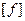- скачок функции на границе раздела двух сред.
Рассмотрим цилиндр, образующие которого перпендикулярны поверхности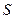 
. По объёму 
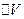проинтегрируем первое и уравнение Максвелла:
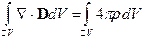
Воспользуемся теоремой Остроградского-Гаусса:
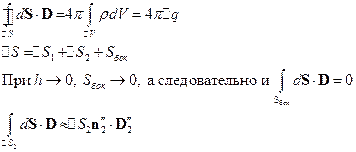
В последнем равенстве мы воспользовались теоремой о среднем.
Аналогично:
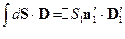
Тогда:
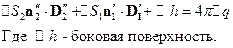
В пределе, при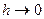 
, 
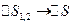
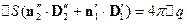
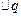- заряд на поверхности раздела двух сред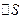 
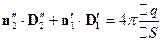
Пусть в пределе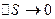 
, при этом
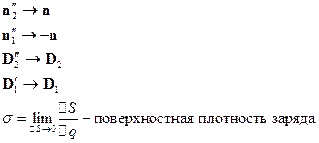
В результате получаем:
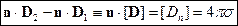
Если на поверхности нет свободных зарядов, то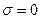 
и 
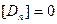, т.е. 
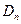- непрерывна.
Аналогично рассмотрев второе уравнение Максвелла
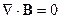
Получим
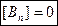
Т.е.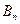 
- всегда непрерывна, её скачок всегда равен нулю.
Теперь рассмотрим четвёртое уравнение Максвелла
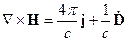
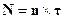
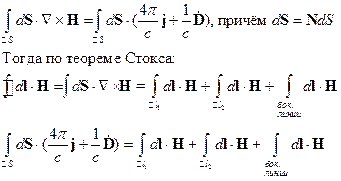
Рассмотрим правую часть этого равенства:
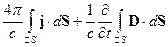
Второе слагаемое, при 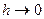даёт 0.
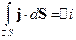- ток, протекающий через поверхность 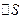, причём ток положителен в направлении нормали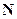 
При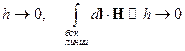 
Воспользуемся теоремой о среднем:
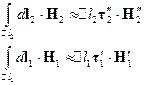
Рассмотрим предельный переход при 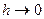, тогда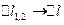 
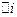- поверхностный ток, текущий через 
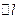перпендикулярно чертежу.
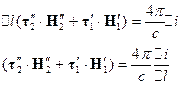
При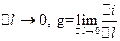 
- ток, текущий по поверхности, в расчёте на длину.
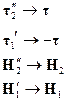
В результате получаем:
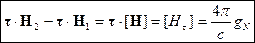
Если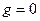 
, то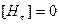 
- непрерывна.
Аналогично для третьего уравнения Максвелла:
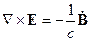
Имеем:
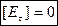
Т.е. тангенциальная составляющая электрического поля непрерывна.
Определим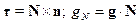 
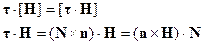
тогда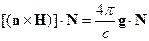 
Ввиду произвольности 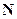, это выражение эквивалентно выражению:
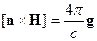
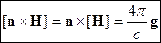
Уравнения Максвелла для стационарного электромагнитного поля в среде.
Поле стационарно, если оно не зависит явно от времени, т.е.
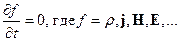
Уравнения Максвелла в этом случаем принимают вид:
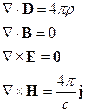
+ связи:
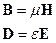
В электростатике используются первое и третье уравнения, а в магнитостатике второе и четвертое.
Связь полей с потенциалами:
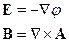
Задачи
1.Определить напряженность электрического поля внутри и снаружи равномерно заряженного шара . Объемная плотность заряда равна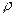 
, радиус шара R.
Решение. Из принципа суперпозиции полей следует, что искомая напряженность поля равна разности напряженности электрического поля, создаваемого шаром без полости, и напряженности поля зарядов, заполняющих при этом полость.
Поле внутри полости
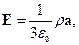
поле внутри шара (но вне полости)
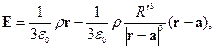
поле снаружи шара
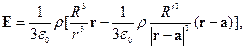
где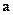 
- радиус-вектор, проведенный из центра шара к центру полости.
2. Определить коэффициенты разложения потенциала точечного заряда в интеграл Фурье.
Решение. Потенциал точечного заряда является решением уравнения
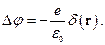(1)
Представим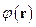 
и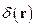 
в виде разложений в интеграл Фурье:
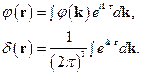(2)
Подставляя соотношения (2) в уравнение (1) и приравнивая в подынтегральных выражениях коэффициенты при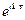 
, получим
.
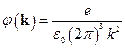3. Найти потенциал, создаваемый зарядом, распределенным в бесконечной среде по закону: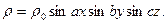 
Решение.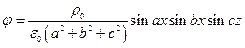 
.
4. Определить потенциал точечного заряда е, находящегося в однородной анизотропной среде с заданным тензором диэлектрической проницаемости.
Решение. Предположив, что заряд расположен в начале координат, решим уравнения
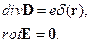
Направим оси декартовой системы координат по главным осям тензора диэлектрической проницаемости. Тогда
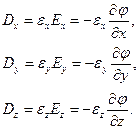
Подставим соотношения (2) в уравнение (1):
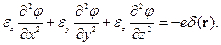
Заменой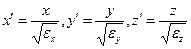 
уравнение приводится к виду
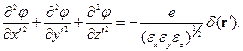
Здесь использовано свойство δ-функции:
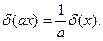
Решение уравнения (4) имеет вид
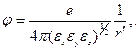
где
