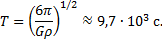Если к силам, действующим на точку, добавить ее силу инерции, то задачу можно решать методами статики, составлением уравнений равновесия

Первая задача динамики для несвободного движения будет обычно сводиться к тому, чтобы, зная движение точки и действующие на нее активные силы, определить реакцию связи.

Методические указания по решению задач.

Решать задачи с применением законов динамики целесообразно следующим образом.

1) Выбрать систему отсчета - инерциальную или неинерциальную.

2) Установить, каким моделям объектов и движений соответствует физическая ситуация, описанная в условии задачи. Сделать рисунок.

3) Назвать все силы, действующие на каждое тело, указывая их происхождение. Изобразить силы на рисунке. Записать законы сил.

4) Записать законы динамики в векторной форме.

5) Выбрать и изобразить на рисунке оси координат. Ось худобно направить по вектору ускорения. Можно для всех тел указать общую систему координат, иногда удобно каждому телу сопоставить свою систему.

6) Записать систему динамических уравнений в проекциях на оси координат.

7) Установить уравнения кинематической связи.

8) Проверить, является ли система уравнений полной, решить ее в общем виде.

9) Проанализировать полученный результат.

Примечание: при решении некоторых задач выполняются не все пункты алгоритма.

Пример 1. При движении автомобиля с постоянным ускорением 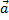, маятник (материальная точка подвешенная на нити) отклоняется от вертикали на угол 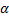(рис.8). Определим с каким ускорением движется автомобиль и натяжение нити.

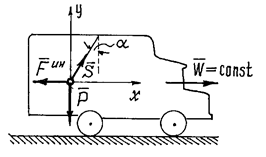
Рис.8

Рассмотрим «динамическое равновесие» точки. Его так называют потому, что на самом деле точка не находится в равновесии, она движется с ускорением.

На точку действуют силы: вес 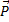и натяжение нити 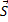, реакция нити. Приложим к точке ее силу инерции 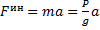, направленную в сторону противоположную ускорению точки и автомобиля, и составим уравнение равновесия:

;

.

Рис. 13.1.

Из второго уравнения следует

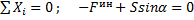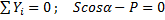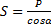
Из первого 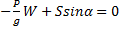и .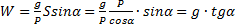

Пример 2.Лифт весом Р (рис.9) начинает подниматься с ускоре­нием a. Определить натяжение троса.

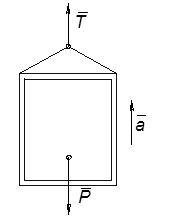
Рис. 9

Рассматривая лифт как свободный, заменяем действие связи (троса) реакцией Т и, составляя уравнение 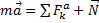в проекции на вертикаль, получаем:

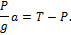
Отсюда находим:

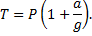
Если лифт начнёт опускаться с таким же ускорением, то натяжение троса будет равно:

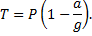
Пример 3.Тело массой 300 кг лежит на полу кабины грузового подъемника, поднимающегося вверх (рис.10). Дано: m=300 кг, а=3 м/с² – ускорение кабины.

Определить силу давления тела на пол кабины Р.

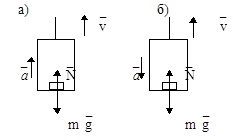
Рис.10

Основной закон динамики для тела запишется в виде:

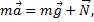
где 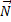- сила реакции опоры.

Рассмотрим два случая:

а) ускорение направлено вверх: ma=N₁–mg,

отсюда N₁=ma+mg.

По третьему закону Ньютона Р₁=N₁ , Р₁= ma+ mg, Р₁=3,84 кН.

б) ускорение направлено вниз: -ma=N₂ - mg,

следовательно N₁=mg–ma, т.е. Р₂=mg- ma, Р₂=2,04 кН.

Пример 4.К нити подвешен груз (рис.11) массой m=1 кг. Найти силу натяжения нити Т, если 1) нить с грузом покоится; 2) двигается вниз с ускорением a= 5 м/с²; 3) двигается вверх с ускорением a= 5 м/с².

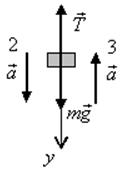
Рис.11

На тело действуют две силы: сила тяжести 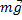и сила натяжения 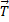. Уравнение движения тела (второй закон Ньютона) в данном случае имеет вид:

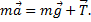
Выберем направление оси y вниз и спроецируем на нее векторы сил и ускорения:

1) 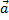=0 ⇒ 0=mg-T ⇒ T=mg=1∙9,8=9,8 Н.

2) 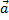направлено вниз ⇒ ma=mg-T ⇒ T=m∙(g-a)=1∙(9,8-5)=4,8 Н.

3) 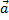направлено вверх ⇒ ma=mg-T ⇒ T=m∙(g+a)=1∙(9,8+5)=14,8 Н.

Пример 5.Груз массой 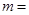50 кг перемещается по горизонтальной плоскости под действием силы F=300 Н, направленной под углом α=30° к горизонтали (рис.12). Коэффициент трения груза о плоскость μ=0,1. Определить ускорение, с которым движется груз.

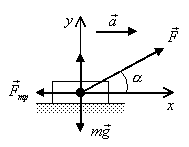
Рис.12

Уравнение движения тела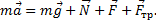

Выберем направления осей х и y и спроецируем на них силы и ускорение:

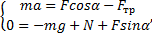
Поскольку F_тр=μN, а из второго уравнения N=mg-Fsinα, то F_тр=μ(mg-Fsinα). Тогда из первого уравнения ускорение

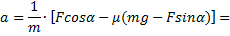
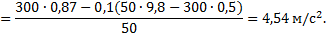
Пример 6. Санки массой m тянут по горизонтальной поверхности с силой F, направленной под углом α к горизонту (рис.12.1). Коэффициент трения между санками и горизонтальной поверхностью равен μ. Определить ускорение санок.

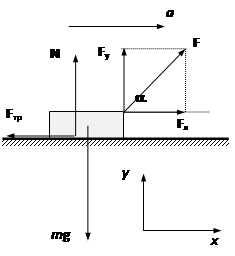
Рис.12.1

Решение.

1. Движение рассматривается относительно Земли, которую считаем инерциальной системой отсчета.

2. В задаче рассматривается поступательное движение твердого тела.

3. На санки действует Земля с силой тяжести mg, веревка с силой F и горизонтальная поверхность с силами нормального давления N и силой трения скольжения F_тр, модуль которой равен

4. Запишем второй закон Ньютона в векторной форме: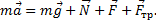

5. Выберем оси координат таким образом, чтобы ось хбыла направлена по вектору ускорения.

6. Спроектируем векторное уравнение на оси координат:

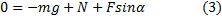
8. В эти три уравнения входят три неизвестных: F_тр,N и а, то есть система уравнений является полной. Разрешим эту систему. Из (3) находим N=mg-Fsinα, из (1) F_тр=μ(mg-Fsinα). Подставляя в (2), получаем

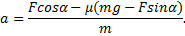
9. Обратим внимание, что сила нормального давления N по величине меньше силы тяжести mg, т.к. вертикальной составляющей силы F санки приподнимаются, а следовательно уменьшается их взаимодействие с горизонтальной поверхностью.

Пример 7.Тело лежит на наклонной плоскости, образующей с горизонтом угол α=5° (рис.13). При каком предельном коэффициенте трения μ_пр тело начнет скользить по наклонной плоскости? С каким ускорением будет двигаться тело, если коэффициент трения μ=0,02? Какое время t понадобиться для прохождения при этих условиях пути s=10 м. Какую скорость тело будет иметь в конце наклонной плоскости?

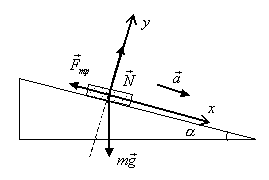
Рис.13

Запишем II закон Ньютона для данного тела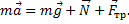

Выбрав оси х и y, спроецируем на них силы и ускорение:

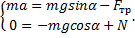
1) Для первого случая, когда μ=μ_пр и a=0, имеем

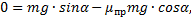
откуда

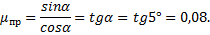
2) Во втором случае μ<μ_пр, поэтому тело будет скользить по наклонной плоскости с ускорением

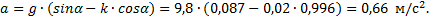
Поскольку тело движется равноускоренно из состояния покоя, то время прохождения им расстояния s=10 м и скорости в конце этого пути можно найти из уравнений кинематики

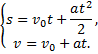
Положив v₀=0. Получим:

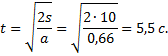
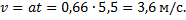
Пример 8. Брусок массы m втаскивают за нить вверх по наклонной плоскости, составляющей угол a с горизонтом (рис.13.1). Сила натяжения нити равна F, угол между нитью и наклонной плоскостью β, коэффициент трения скольжения между бруском и плоскостью равен μ. Найти ускорение бруска.

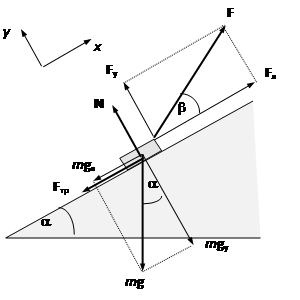
Рис.13.1

Решение.

1) В задаче описано поступательное движение бруска относительно Земли, которую считаем инерциальной системой отсчета.

2) На брусок действуют:

- Земля с силой тяжести mg;

- нить с силой F;

- наклонная плоскость с силами нормального давления N и трения F_тр, причем,

3) По второму закону Ньютона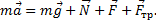

4) Направим ось х вверх вдоль наклонной плоскости (по ускорению в соответствии с условием задачи).

5) Спроектируем векторное уравнение на оси координат:

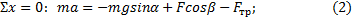
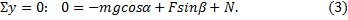
6) Получена система трех уравнений с тремя неизвестными. Из (3) находим величину силы нормального давления 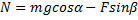, из (1) - величину силы трения 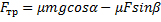. Подставляя полученное выражение в (2), находим искомое ускорение

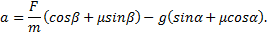
Пример 9.Под действием силы F = 10 Н тело движется прямолинейно так, что зависимость пройденного телом пути S от времени t дается уравнением S=A-Bt+Ct², где С = 1 м/с². Найти массу m тела.

Решение. 1) Известно, что зависимость пути от времени выражается формулой:

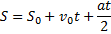
Отсюда имеем:

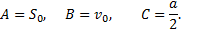
2) По условию: C=1 м/с² следовательно: a=2C=2 м/с²

3) Из второго закона Ньютона: F=ma отсюда: m=F/a=10/2=5 кг.

Пример 10. Ледяная горка составляет с горизонтом угол α (рис.14). По ней пускают вверх камень, который после подъема съезжает вниз. Дано: t₂/t₁=n.

Чему равен коэффициент трения μ, если время спуска в n раз больше времени подъема.

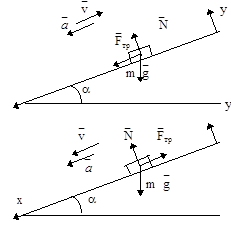
Рис.14

Решение. Уравнение движения камня

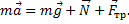
При движении вверх - движение равнозамедленное. В проекциях на оси ОХ и OY: ma₁=F_тр+mg∙sinα; N-mg∙cosα=0,

откуда N= mg∙cosα. Тогда сила трения F_тр =μN=μmg∙cosα, и окончательно уравнение движения

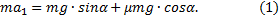
При движении вниз: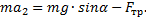

Проведя аналогичные преобразования, получим уравнение движения в этом случае:

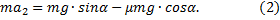
Из (1) и (2):

При движении вверх камень проходит путь 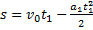; скорость в конце подъема v=0, следовательно v_o= a₁t₁, тогда

При движении вниз камень проходит путь

Из (3) и (4) получим

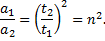
Используя (1) и (2):

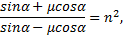
отсюда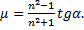

Пример 11. На рис.14.1,а изображен качающийся маятник, на рисунке 14.1,б - конический маятник. Верно ли представлено соотношение сил mg и Т на рисунках 14.1,а и 14.1,б?

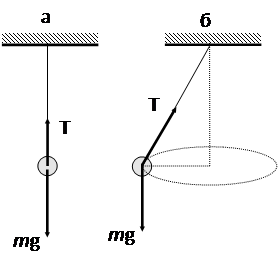
Рис.14.1

Решение. В обоих случаях материальная точка движется по окружности. Вектор полного ускорения складывается из нормального ускорения a_n, направленного к центру окружности, и тангенциального a_τ, направленного по касательной к окружности. По второму закону Ньютона ускорение определяется равнодействующей силой, то есть ma=mg+T. Направления равнодействующей силы и ускорения совпадают.

В случае 14.1,а равнодействующая сила ориентирована вертикально, поэтому a_τ =0 и полное ускорение равно нормальному ускорению, a = a_n. Оно направлено к центру окружности, то есть вверх. Поэтому сила натяжения нити по величине должна быть больше силы тяжести. Соотношения между силами представлены неверно.

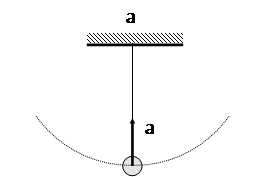
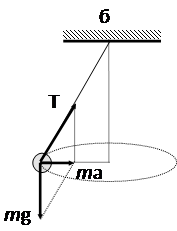
В случае 14.1,б материальная точка движется по окружности с постоянной скоростью. Ускорение при таком движении направлено к центру окружности. Во втором законе Ньютона ma=mg+T силы являются сторонами параллелограмма, а ma - его диагональю. Произведя на рисунке сложение векторов, можно сделать вид, что соотношения между силами представлены правильно.

Пример 12. Для материальной точки, движущейся по окружности, дан график зависимости скорости от времени v(t) (рис.15). Указать направление результирующей силы, действующей на материальную точку в положении М.

Рис.15

Решение. Скорость направлена по касательной к траектории. Из графика видно, что в момент времени t_M величина скорости уменьшается, поэтому тангенциальное ускорение a_𝛕 противоположно вектору скорости. Нормальное ускорение a_n направлено к центру окружности.

Рис.15.1

Изобразим вектор полного ускорения a=a_n+a_τ (рис.15.1). Направление равнодействующей силы совпадает с вектором полного ускорения.

Пример 13. Два маленьких шарика, массы которых равны m₁ и m₂, привязаны к нити один за другим и вращаются в горизонтальной плоскости с угловой скоростью ω (рис.16). Расстояния от шариков до оси вращения l₁ и l₂. Определить силы натяжения нитей.

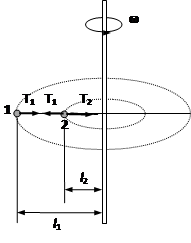
Рис.16

Решение. Поскольку силой тяжести в данной задаче можно пренебречь, (по условию шарики вращаются в горизонтальной плоскости), будем считать, что на шарики действуют только нити: на шарик 1 одна нить с силойT₁, на шарик 2 - две нити с силами T₁ и T₂.

Запишем второй закон Ньютона сразу в проекциях на рaдиальное направление.

Для шарика 1: m₁a₁=T₁, (1)

для шарика 2: m₂a₂=T₂-T₁. (2)

Существенным условием данной задачи является равномерное движение материальных точек по окружности. При таком движении линейные скорости шариков не меняются по величине, а следовательно, тангенциальное ускорение равно нулю. Вектор полного ускорения направлен к центру окружности, а его величина связана с угловой скоростью ω и радиусом окружности r соотношением

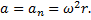
Таким образом, величина ускорения каждого шарика соответственно равна 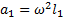и 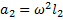. С учетом этих соотношений уравнения динамики (1) и (2) примут вид

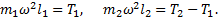
Отсюда получаем выражения для искомых сил:

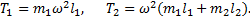
Пример 14.Автомобиль массой m = 5 тонн проходит по выпуклому мосту со скоростью v=36 км/ч (рис.17). С какой силой F он давит на середину моста, если радиус кривизны моста R=100 м? Какова будет сила давления, если мост будет вогнутый с тем же радиусом кривизны?

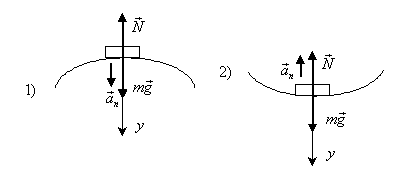
Рис.17

Решение.На основании II закона Ньютона запишем уравнение движения автомобиля:

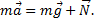
Выберем направление оси y и спроецируем на нее силы и ускорение. Обратим внимание на то, что поскольку движение автомобиля равномерное криволинейное, то ускорение

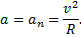
По III закону Ньютона сила, с которой автомобиль давит на мост, равна по модулю силе, с которой мост давит на автомобиль, т.е. силе нормальной реакции опоры N.

1) Уравнение движения в проекциях для первого случая имеет вид

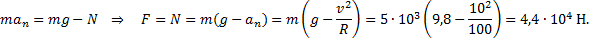
2) Для второго случая

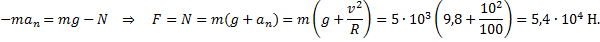
Пример 15. На сколько должен быть поднят наружный рельс над внутренним (рис.18) на закруглении железнодорожного пути радиусом 300 м, если ширина колеи 1524 мм? Скорость, при которой сила давления на рельсы перпендикулярна им, принять равной 54 км/ч.

Дано: R=300 м, l=1,524 м, v=15 м/с.

Найти: h - ?

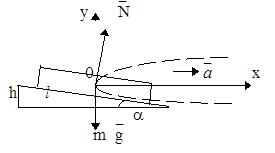
Рис.18

Решение. Поезд должен двигаться по окружности радиуса R со скоростью v, т.е. с ускорением a=v²/R, направленным горизонтально. Это ускорение вызывает равнодействующая сил 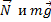. Поэтому наружный рельс должен быть приподнят на некоторую высоту h.

Второй закон Ньютона

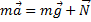
в проекциях на оси ОХ и OY:

ma = N∙sinα,

N∙cosα - mg = 0.

Откуда

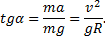
Так как угол α мал, то sinα≈tgα.

Из рис.18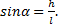

Следовательно,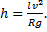

h=0,12 м.

Пример 16. На экваторе некоторой планеты тело весит вдвое меньше, чем на полюсе P=Р_п/2 (рис.19). Плотность вещества этой планеты ρ=3∙10³ кг/м³. Определить период вращения планеты T вокруг своей оси.

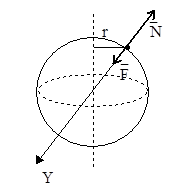
Рис.19

На тело, находящееся на поверхности планеты, действуют: 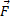- сила тяготения со стороны планеты, 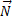– сила нормальной реакции планеты (рис.19).

По определению, 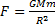, где М - масса планеты, m - масса тела, R-радиус планеты.

Масса планеты: 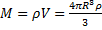, а

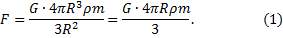
По второму закону Ньютона: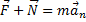

в скалярной форме относительно оси Y:

F – N = ma_n, (2)

или

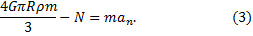
Рассмотрим два частных случая движения тела.

1. Тело находится на полюсе, т.е. r=0, тогда линейная скорость тела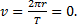

Следовательно, уравнение (3) примет вид 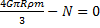, откуда

N_п - сила нормальной реакции на полюсе.

2. Тело находится на экваторе. В этом случае r=R и v=2πr/T. Тогда уравнение (3) примет вид: 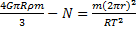, откуда

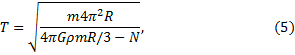
где N - сила нормальной реакции поверхности на экваторе.

По условию задачи, Р_э=Р_п/2.

Поскольку Р=N, то N=N_п/2, или с учетом (4)

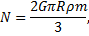
Подставим формулу (6) в (5):