Полярна система координат
При геодезичних вимірюваннях на місцевості в основному використовуються полярні координати. В аналітичній геометрії цілий ряд ліній краще досліджувати і будувати в полярній системі координат.
Полярна система координат на площині вводиться за допомогою полярної осі (початок координат називається полюсом) та кута повороту цієї осі (додатним вважається напрям проти стрілки годинника) (рис. 36)
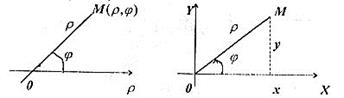
Рис. 36. Рис. 37.
Координати точки в такій системі мають вигляд 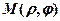 . Якщо необмежувати значень
. Якщо необмежувати значень 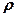 і
і 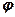 , то точки
, то точки 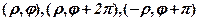 збігаються, тобто між множиною точок площини і множиною пар чисел
збігаються, тобто між множиною точок площини і множиною пар чисел 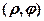 немає взаємно однозначної відповідності. Для того щоб така відповідність існувала, треба розглядати так звані головні значення полярних координат, тобто
немає взаємно однозначної відповідності. Для того щоб така відповідність існувала, треба розглядати так звані головні значення полярних координат, тобто 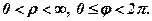 Надалі розглядаються тільки такі значення.
Надалі розглядаються тільки такі значення.
Зв’язок між полярними та прямокутними координатами легко зрозуміти з рис. 37, а саме,
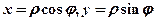 (45)
(45)
і навпаки, полярні координати виражаються через прямокутні
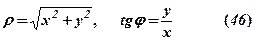
Щоб знайти 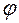 в (46) враховуємо збіг знаків
в (46) враховуємо збіг знаків 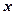 і
і 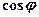 , а також
, а також 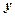 і
і 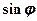 .
.
Наводимо графіки деяких ліній в полярних координатах.
Промінь. Нехай промінь виходить з полюса під кутом 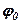 до полярної осі. Тоді рівняння променя (див. рис. 38).
до полярної осі. Тоді рівняння променя (див. рис. 38).
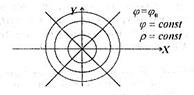
Рис. 38.
Коло. Радіуса 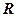 , центр якого в полюсі, має рівняння
, центр якого в полюсі, має рівняння
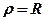 .
.
Спіраль Архімеда має вигляд 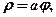 де
де 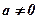 – задане дійсне число.
– задане дійсне число.
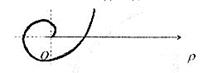
Рис. 39.
Кардіоїда описується рівнянням 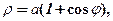 де
де 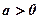 задане
задане
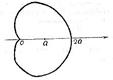
Рис. 40.
Розаминазиваються лінії, які задаються рівняннями
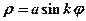 або
або 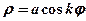 ,
,
де 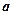 і
і 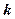 – додатні числа.
– додатні числа.
Оскільки 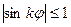 ,
, 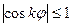 , то із рівнянь випливає, що
, то із рівнянь випливає, що 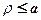 а це означає, що вся лінія розміщена усередині круга радіуса
а це означає, що вся лінія розміщена усередині круга радіуса 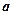 . Функція
. Функція 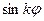 (
( 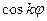 ) – періодична, і її графік складається з однакових пелюсток, кожна з яких симетрична відносно найбільшого значення полярного радіуса
) – періодична, і її графік складається з однакових пелюсток, кожна з яких симетрична відносно найбільшого значення полярного радіуса 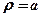 . Кількість пелюсток залежить від числа k:
. Кількість пелюсток залежить від числа k:
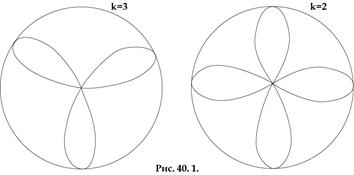
при k -цілому і непарному роза складається із k пелюсток;
при k -цілому і парномуроза складається із 2k пелюсток(див. рис. 40,1).
|
Задача. Побудувати в полярних координатах графік функції 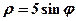 , записавши таблицю значень
, записавши таблицю значень 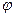 у градусах з кроком в
у градусах з кроком в 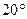 . Перейти у рівнянні
. Перейти у рівнянні 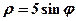 до декартових координат.
до декартових координат.
Розв’язання.Заповнимо таблицю значень аргумента 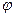 і функції
і функції 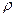
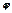 | 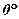 | 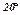 | 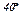 | 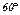 | 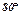 | 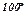 | 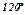 | 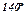 | 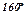 | 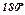 |
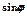 | 0,3420 | 0,6428 | 0,8660 | 0,9848 | 0,9848 | 0,8660 | 0,6428 | 0,3420 | ||
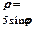 | 1,71 | 3,21 | 4,33 | 4,92 | 4,92 | 4,33 | 3,21 | 1,71 |
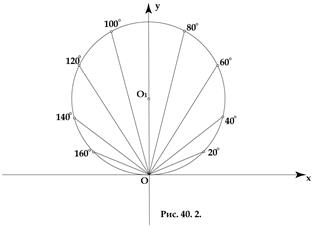
За даними таблиці будуємо точки в полярній системі координат і з’єднуємо їх плавною лінією.
Перейдемо у рівнянні 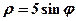 від полярних координат до декартових за допомогою формули переходу (45) і (46)
від полярних координат до декартових за допомогою формули переходу (45) і (46)
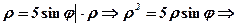
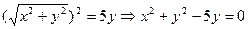 , - це коло.
, - це коло.
Щоб знайти центр і радіус кола, виділимо повний квадрат:
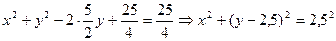 .
.
Центр кола в точці 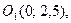 радіус
радіус 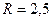 (див. рис.)
(див. рис.)
|
Для побудови графіка провели промені під відповідними кутами: 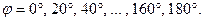 На кожному з променів відкладається відповідне значення
На кожному з променів відкладається відповідне значення 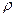 , взяте із таблиці:
, взяте із таблиці: