Законы Ома и Джоуля-Ленца в интегральной и дифференциальной формах. Зав-сть сопротивления от температуры

Немецкий физик Г.Ом (1787-1854) экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника 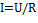(98.1), где R – электрическое сопротивление проводника.

Закон Ома для участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника

Закон Ома можно представить в дифференциальной форме.

Подставив выражение 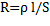в (98.1), получим 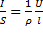(98.3) , где величина обратная удельному сопротивлению, 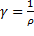называется удельной электрической проводимостью вещества проводника.

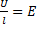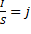, формулу (98.3) можно записать в виде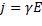

Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора 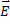, то направления 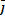и 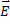совпадают. Поэтому формулу можно записать в виде 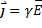. Это выражение – закон Ома в дифференциальной форме, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке.

Опыт показывает, что изменение удельного сопротивления и сопротивления проводника при t и 0^оС. Следовательно, температурная зависимость сопротивления может быть представлена в виде R=αR_oT.

Зависимость сопротивления от температуры представлена на рисунке (кривая 1). При низких температурах наблюдается от этой зависимости. Впоследствии было обнаружено, что сопротивление многих металлов и сплавов при очень низких температурах Т_к, называемых критическими, характерных для каждого вещества, скачкообразно уменьшается до 0 (кривая 2), т. Е. металл становится абсолютным проводником. Впервые это явление, названное сверхпроводимостью, обнаружено в 1911 г. Г. Камерлинг-Оннесом для ртути.

На зависимости электрического сопротивления металлов от t основано действие термометров сопротивления, кот. Позволяют измерять t с точностью до 0,001 К.

Рассмотрим однородный проводник, к концам которого приложено напряжение U.

За время dt через сечение проводника переносится заряд dq — Idt. При этом силы электростатического поля и сторонние силы совершают работу (99.1)

Если сопротивление проводника R, то, используя закон Ома (98.1), получим, что работа тока

Из (99.1) и (99.2) следует, что мощность тока

Если ток проходит по неподвижному металлическому проводнику, то вся работа идет на его нагревание и, но закону сохранения энергии, dQ = dA. (99.4)

Таким образом, используя выражения (99.4), (99.1) и (99.2), получим dQ = IUdt = PRdt = (U²/R)dt. (99.5)

Выражение (99.5) представляет собой закон Джоуля —Ленца, экспериментально установленный независимо друг от друга Дж. Джоулем и Э. X. Ленцем.

Количество теплоты, выделяющееся за единицу времени в единице объема, называется удельной тепловой мощностью тока. Она равна w = pf. (99.6)

Используя дифференциальную форму законаи соотношение 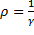, получим w = jE = 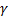E². (99.7)

Формулы (99.6) и (99.7) являются обобщенным выражением закона Джоуля —Ленца в дифференциальной форме, пригодным для любого проводника.