Непрерывность функции в точке и на отрезке

Пусть функция 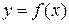определена на некотором множестве X и точка 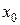является предельной точкой, принадлежащей этому множеству.

Определение 3.1.1. Функция 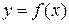называется непрерывной в точке 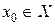, если она определена в точке 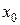и в некоторой ее окрестности существует предел функции при 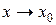и он равен значению функции в этой точке, т.е.

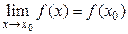. (3.1)

Равенство (3.1) означает выполнение трех условий:

1) функция 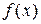определена в точке 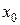и в ее окрестности;

2) функция 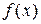имеет предел при ;

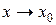3) предел функции в точке 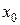равен значению функции в этой точке, т.е. выполняется равенство (3.1).

Можно дать еще одно определение непрерывности функции, опираясь на понятия приращения аргумента и функции.

Пусть функция 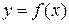определена в некотором интервале 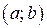. Возьмем произвольную точку 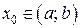. Для любого 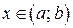разность 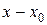называется приращением аргумента x в точке 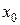и обозначается 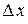(«дельта x»): 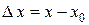. Отсюда .

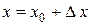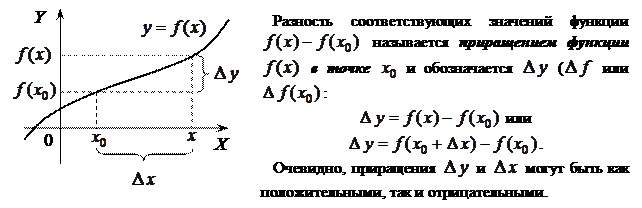
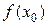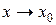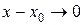В равенстве (3.1), внося под знак предела и учитывая, что условия и равносильны, получаем

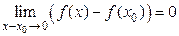
Тогда в приведенных обозначениях полученное равенство примет вид:

,

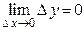которое и является определением непрерывности функции в точке.

Определение 3.1.2. Функция 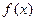называется непрерывной в точке 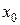, если ее приращение в этой точке является бесконечно малой функцией при 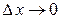( 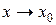), т.е.

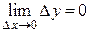. (3.2)

Пример 3.1. Доказать, что функция 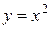непрерывна в любой точке 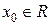, т.е. в любой точке области определения.

Решение. Дадим аргументу приращение 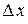в точке 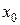. Тогда функция получит приращение:

.

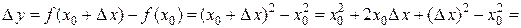
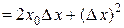Следовательно, 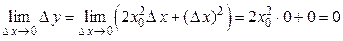, т.е. 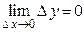, а это и означает, что функция 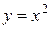непрерывна в точке .

,

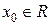Рассмотрим основные теоремы о непрерывных функциях, которые примем без доказательства.

Теорема 3.1. (арифметические действия над непрерывными функциями) Если функци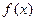и и 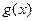непрерывны в точке 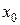, то функци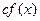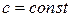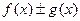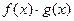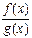и ( ), , , (если 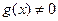) также непрерывны в точке .

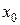Теорема 3.2. (непрерывность сложной функции) Пусть функция 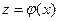непрерывна в точке 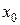, а функция 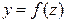непрерывна в точке 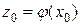, тогда сложная функция 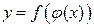непрерывна в точке .

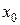Определение 3.2. Функция 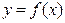называется непрерывной в интервале 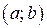, если она непрерывна в каждой точке этого интервала.

Определение 3.3. Функция 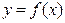называется непрерывной на отрезке 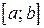, если она непрерывна в интервале 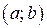и в точке 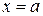непрерывна справа (т.е. 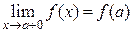), а в точке 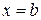непрерывна слева (т.е. ).

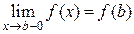Теорема 3.3. Если функция 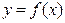определена, строго монотонна и непрерывна на отрезке 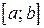, то обратная функция 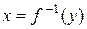определена, строго монотонна и непрерывна на отрезк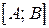е , где .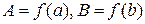

3.2.Точки разрыва функции и их классификация

Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если 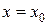– точка разрыва функции 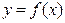, то в ней не выполняется по крайней мере одно из условий определения 3.1.1. непрерывности функции, а именно:

1) функция определена в окрестности точки 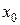, но не определена в самой точке ;

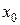2) функция определена в точке 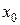и ее окрестности, но не существует предела 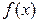при ;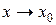

3) функция определена в точке 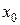и ее окрестности, существует 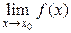, но этот предел не равен значению функции в точке : .

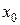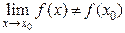Все точки разрыва функции разделяются на точки разрыва первого и второго рода.

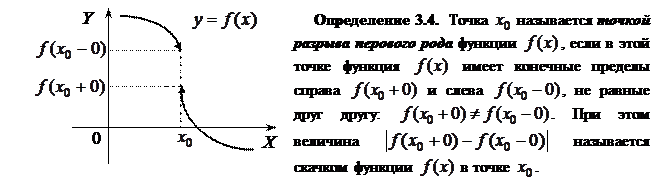
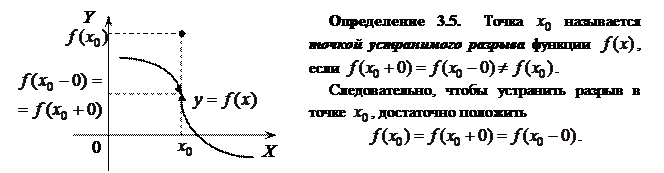
Определение 3.6. Если 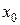– точка разрыва функции 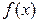и хотя бы один из односторонних пределов 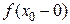, 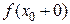равен бесконечности или не существует, то 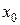называется точкой разрывавторого рода.

Пример 3.2. Исследовать на непрерывность функцию

.

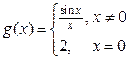Решение. Данная функция определена в любой точке множества R, кроме 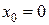, которая является точкой разрыва

.

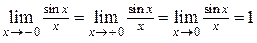Но 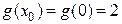. Значит, точка 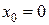– есть точка разрыва первого рода.

А так как 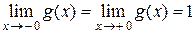, то это точка устранимого разрыва. Положив 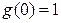(вместо 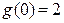) при 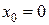, разрыв устраняется, функция становится непрерывной.

,

Пример 3.3. Исследовать на непрерывность функцию

.

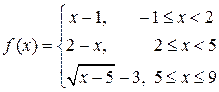Решение. Функция 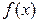определена и непрерывна на промежутках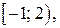 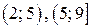, где она задана непрерывными элементарными функциями. Следовательно, разрыв возможен только в точках 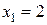и .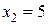

1) Для точки 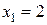имеем:

, .

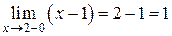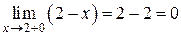т.е. функция 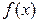в точке 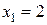имеет разрыв первого рода. Скачок функции равен .

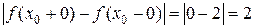2) Для точки 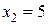имеем:

, , .

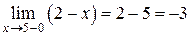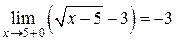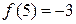т.е. функция 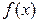в точке 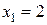непрерывна.

,

Пример 3.4. Исследовать на непрерывность функцию

.

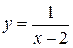Решение. Функция 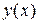определена и непрерывна на интервалах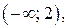 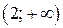. Следовательно, разрыв возможен только в точке .

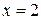Для точки 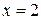имеем:

, .

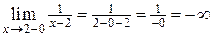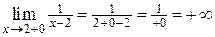т.е. функция 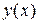в точке 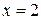имеет разрыв второго рода. ,

3.3.Свойства функций, непрерывных на отрезке

Если функция 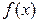определена на множестве X и существует такое число 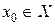, что для всех 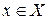выполняется условие 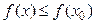( 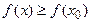), то число 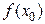называется наибольшим (наименьшим) значением функции 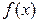на множестве X.

Непрерывность на отрезке функции обладают рядом важных свойств, выражаемые следующими теоремами, которые примем без доказательства.

Теорема 3.4. (первая теорема Вейерштрасса) Если функция 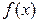непрерывна на отрезке 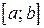, то она ограничена на этом отрезке.

Теорема становится неверной, если в ней отрезок 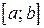заменить интервалом 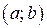или полуинтервалом 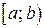, либо 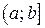. Например, функция 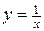на интервале 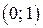непрерывна, но не является на нем ограниченной, так как .

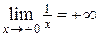Теорема 3.5. (вторая теорема Вейерштрасса) Если функция 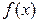непрерывна на отрезке 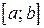, то она достигает на этом отрезке своего наименьшего значения m и наибольшего значения M, т.е. существуют точки 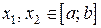, такие, что .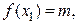

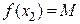Заметим, что точки 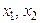, в которых достигаются наименьшее и наибольшее значения функции 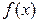на отрезке 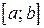, не обязательно должны быть единственными.

Теорема 3.5. имеет простой геометрический смысл. Она утверждает, что значения непрерывной на отрезке 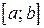функции заключены между ее наименьшим и наибольшим значениями, т.е. .

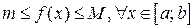Если функция 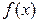непрерывна на интервале 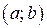, то она может не достигать наименьшего и наибольшего значений на нем. Например, функция 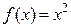на интервале 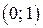не достигает значени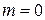й и 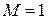, так как эти значения функции принимает в точках 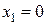и 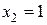, а эти точки данному интервалу не принадлежат.

Теорема 3.6. (Больцано - Коши о промежуточном значении) Если функция 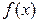непрерывна на отрезке 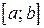и 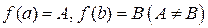, то каково бы ни было число C, заключенное между A и B, найдется точка 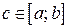, такая, что .

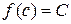Следствие. Если функция 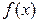непрерывна на отрезке 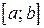и на его концах принимает значения разных знаков, то на этом отрезке существует хотя бы одна точка 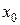, в которой функция обращается в нуль, т.е. .

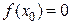Пример 3.5. Доказать, что на отрезке 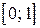уравнение 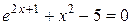имеет хотя бы один действительный корень.

Решение. Рассмотрим функцию 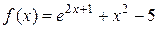. Имеем

;

.

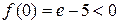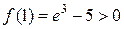Следовательно, найдется хотя бы одна точка 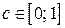, что 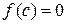. Значит, c – корень уравнения.

,