Операторы в линейных пространствах.

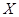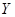Пусть и - два произвольных линейных пространства. Как известно, оператором, действующим из 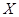в 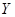называется отображение пространства 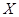в пространство 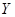. Если отображение обозначить символом 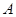, то это записывают так:

.

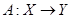Образ вектора 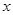обозначают 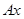или 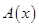и называют значением оператора 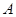на векторе 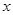. По определению .

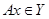Оператор 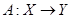называют линейным оператором, есл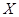и и 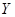- пространства над одним и тем же полем 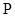и при этом

1.

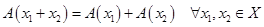
(аддитивность оператора);

2.

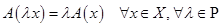
(однородность оператора).

Понятие линейного оператора является одним из важнейших в математике. Это подтверждается хотя бы тем, что основные операторы, изучаемые в математическом анализе и алгебре (предельный переход, дифференцирование, интегрирование, проектирование на подпространство, умножение на матрицу и др.) являются линейными.

Оператор 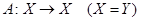называют также преобразованием пространства .

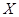Основные типы задач по этой теме:

a) проверка линейности заданного оператора;

b) нахождение образа, ядра, ранга и дефекта линейного оператора;

c) построение матрицы линейного оператора в данных базисах (в данном базисе);

d) нахождение собственных значений и собственных векторов линейного оператора (№№1465-1484);

e) построение канонического базиса и жордановой нормальной формы линейного оператора (№№1529-1536).

Основная трудность задач первой группы состоит в том, что примеры операторов могут быть взяты из различных разделов математики и требуют от студента эрудиции и определенной математической культуры. Приведем несколько примеров.

Задача 3.1. Проверьте линейность следующих операторов:

1. .

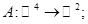
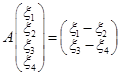2. 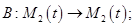( 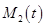-пространство многочленов степени 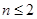над некоторым полем).

.

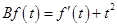3. .

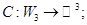
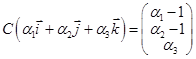4. .

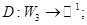
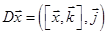5. .

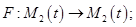
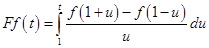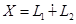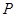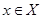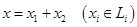6. . Определим оператор так: если и , то 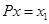(оператор проектирования на 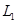параллельно ).

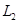7. 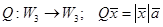( 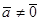- фиксированный вектор).

Решение.

1. 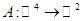является отображением. Проверим аддитивность и однородность.

.

.

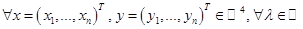
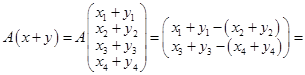
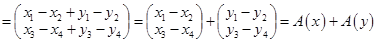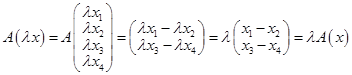Все условия выполнены, значит, 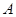является линейным оператором.

5. .

,

.

.

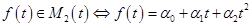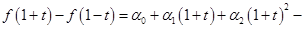
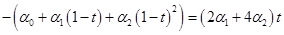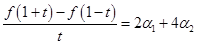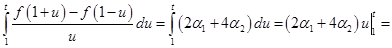
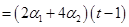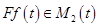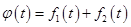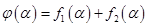. Теперь проверяем аддитивность и однородность. Напомним: если , то и .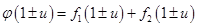

Находим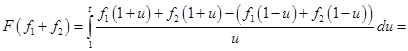

.

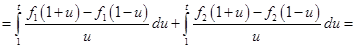
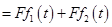Точно так же

.

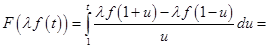
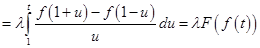Все условия определения линейного оператора выполнены.

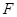- линейный оператор.

Линейный оператор нулевой вектор отображает в нулевой ( 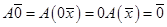). Поэтому, если 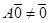, то 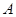нелинейный. Рекомендуем в подозрительных случаях прежде, чем начинать проверку аддитивности и однородности, вычислить значение оператора на нулевом векторе. Так в упражнении 2 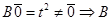- нелинейный. В упражнении 3 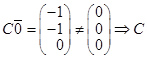- нелинейный.

Для доказательства нелинейности достаточно привести пример двух векторов, для которых нарушена аддитивность, или пример вектора или скаляра, для которых не выполнена однородность (равенство 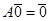может иметь место и для нелинейных операторов). Например: в упражнении 7 настораживает то, что текущий вектор 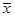находится под знаком 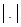. Поэтому проверку ведем на конкретных векторах.

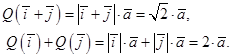
Очевидное неравенство 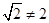доказывает неаддитивность 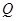и его нелинейность.

В этом же примере можно поступить и так:

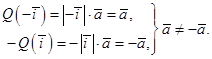
Поэтому оператор 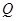неоднороден, следовательно, и нелинеен.

Проверку линейности операторов из упражнений 4 и 6 предоставляем читателю.

Чтобы глубже понять определение линейного оператора, придумайте примеры:

1. оператора аддитивного, но не однородного;

2. оператора однородного, но не аддитивного.